|
Last time we introduced angular velocity with regard to flywheels and how a fixed point riding piggyback on a moving flywheel travels the same circular path as its host at a pace that’s measured in units of degrees per second. Today we’ll introduce another unit of measure, the radian, and see how it’s uniquely used to measure angles of circular motion in units of radians per second. Radians and the Angular Velocity of a Flywheel
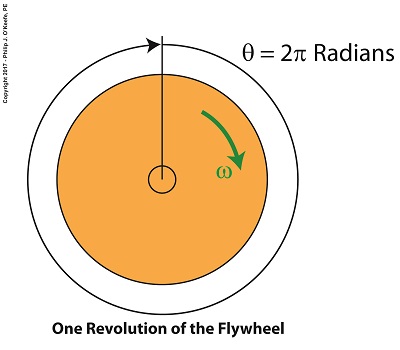
Back in elementary school we worked with protractors and measured angles in degrees, and we were all too familiar with the fact that the average protractor maxed out at 180, or half the degrees present in a complete circle. But in the grownup worlds of physics and engineering, angles of circular motion are measured in units called radians, an international standard equal to 57.3 degrees that’s used to measure objects rotating in circular motion. If we divide a circle’s value of 360 degrees by the 57.3 degrees that represent a radian, we find there are 6.28 radians in a circle, and oddly enough, it just so happens that 6.28 is equal to 2 × π. Anyone who stayed awake during math class can’t help but remember that π represents a constant value of 3.14, a number that pops up anytime you divide the circumference of a circle by its diameter. No matter the circle’s size, π will always result when you perform this operation. Applying these facts to radians, we find that during one complete revolution of a flywheel the measure of the angle θ increases from 0 radians to 2π radians. Suppose we have a flywheel spinning at N revolutions per minute, or RPMs. To calculate the angular velocity, ω, of any point on the flywheel, or the whole wheel for that matter, we use the following formula which provides an answer in radians per second, ω = [2 × π × N ] ÷ 60 seconds/minute (1) If a flywheel spins at 3000 RPM, its angular velocity is calculated as, ω = [2 × π × (3000 RPM)] ÷ 60 seconds/minute (2) ω = 314.16 radians/second (3) Next time we’ll see how angular velocity is used to determine the kinetic energy contained within a flywheel.
Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |