Archive for the ‘Personal Injury’ Category
Monday, November 6th, 2017
|
Last time we arrived at a general formula to compute the kinetic energy, KE, contained within the totality of a spinning flywheel made up of numerous parts. Today we’ll discuss the terms in that formula, which encompasses a phenomenon of flywheels known as moment of inertia.
Moment of Inertia in a Flywheel
The kinetic energy formula we’ve been working with is, again,
KE = ½ × Σ[m × r2] × ω2 (1)
The bracketed part of this equation makes reference to spinning flywheels comprised of one or more parts, and that’s what we’ll be focusing on today. The symbol Σ is the Greek letter sigma, standard engineering shorthand notation used to represent the sum of all terms and mathematical operations contained within the brackets.
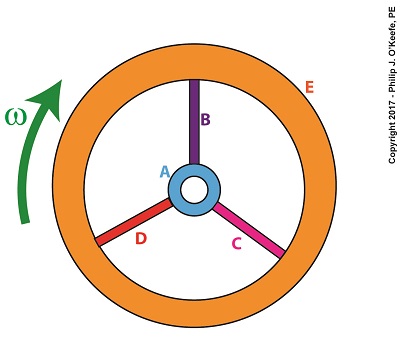
Our illustration shows we have five parts to consider: a hub, three spokes and a rim, and label them A, B, C, D, and E respectively. Each part has its own mass, m, and is a unique distance, r, from the flywheel’s center of rotation. The flywheel’s angular velocity is represented by ω.
For our flywheel of parts A through E our expanded equation becomes,
Σ[m × r2] = [mA × rA2] + [mB × rB2] + [mC × rC2] + [mD × rD2] + [mE × rE2] (2)
Equation (2) represents the sum total of moments of inertia contained within our flywheel. It’s a numerical representation of the flywheel’s degree of resistance to changes in motion.
The more mass a flywheel has, the greater its moment of inertia. When at rest this greater moment of inertia means it will take more effort to return it to motion. But once in motion the flywheel’s greater moment of inertia will make it harder to stop. That’s because there’s a lot of kinetic energy stored within its spinning mass, and the heavier a flywheel is, the more kinetic energy it contains. In fact, for any given angular velocity ω, a large and heavy flywheel stores more kinetic energy than a smaller, lighter flywheel.
But there’s more to a flywheel’s moment of inertia than just mass. What’s really important is how that mass is distributed. We’ll get into that next time when we discuss torque.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: angular velocity, center of rotation, engineering, flywheel, kinetic energy storage, mass, moment of inertia, spinning flywheel
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Moment of Inertia in a Flywheel
Thursday, October 26th, 2017
|
Last time we introduced the fact that spinning flywheels are subject to both linear and angular velocities, along with a formula that allows us to calculate these quantities for a single part of the flywheel, designated A. We also re-visited the kinetic energy formula. Today we’ll build upon those formulas as we attempt to answer the question, How much kinetic energy is contained within a spinning flywheel?
Here again is the basic kinetic energy formula,
KE = ½ × m × v2 (1)
where, m equals a moving object’s mass and v is its linear velocity.
Here again is the formula used to calculate linear and angular velocities for a single part A within the flywheel, where part A’s linear velocity is designated vA, angular velocity by ω, and where rA is the distance of part A from the flywheel’s center of rotation.
vA = rA × ω (2)
Working with these two formulas, we’ll insert equation (2) into equation (1) to obtain a kinetic energy formula which allows us to calculate the amount of energy contained in part A of the flywheel,
KEA = ½ × mA × (rA × ω)2 (3)
which simplifies to,
KEA = ½ × mA × rA2 × ω2 (4)
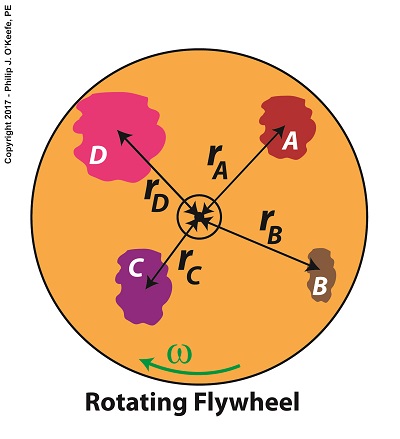
Equation (4) is a great place to begin to calculate the amount of kinetic energy contained within a spinning flywheel, however it is just a beginning, because a flywheel contains many parts. Each of those parts has its own mass, m, and is a unique distance, r, from the flywheel’s center of rotation, and all these parts must be accounted for in order to arrive at a calculation for the total amount of kinetic energy contained within a spinning flywheel.
How Much Kinetic Energy is Contained Within a Spinning Flywheel?
Put another way, we must add together all the m × r2 terms for each and every part of the entire flywheel. How many parts are we speaking of? Well, that depends on the type of flywheel. We’ll discuss that in detail later, after we define a phenomenon that influences the kinetic energy of a flywheel known as the moment of inertia.
For now, let’s just consider the flywheel’s parts in general terms. A general formula to compute the kinetic energy contained within the totality of a spinning flywheel is,
KE = ½ × ∑[m × r2] × ω2 (5)
We’ll discuss the significance of each of these variables next time when we arrive at a method to calculate the kinetic energy contained within all the many parts of a spinning flywheel
.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: angular velocity, center of rotation, engineering, flywheel, kinetic energy, linear velocity, mass, moment of inertia
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on How Much Kinetic Energy is Contained Within a Spinning Flywheel?
Thursday, October 19th, 2017
|
Anyone who has spun a potter’s wheel is appreciative of the smooth motion of the flywheel upon which they form their clay, for without it the bowl they’re forming would display irregularities such as unattractive bumps. The flywheel’s smooth action comes as a result of kinetic energy, the energy of motion, stored within it. We’ll take another step towards examining this phenomenon today when we take our first look at calculating this kinetic energy. To do so we’ll make reference to the two types of velocity associated with a spinning flywheel, angular velocity and linear velocity, both of which engineers must negotiate anytime they deal with rotating objects.
Let’s begin by referring back to the formula for calculating kinetic energy, KE. This formula applies to all objects moving in a linear fashion, that is to say, traveling a straight path. Here it is again,
KE = ½ × m × v2
where m is the moving object’s mass and v its linear velocity.
Flywheels rotate about a fixed point rather than move in a straight line, but determining the amount of kinetic energy stored within a spinning flywheel involves an examination of both its angular velocity and linear velocity. In fact, the amount of kinetic energy stored within it depends on how fast it rotates.
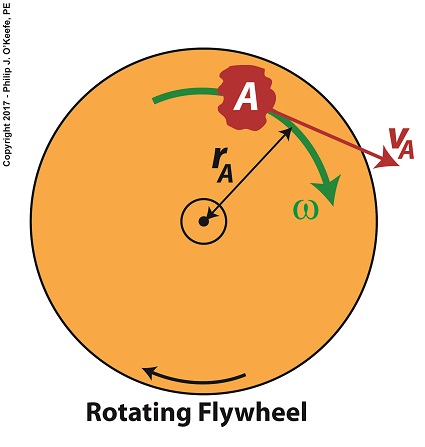
For our example we’ll consider a spinning flywheel, which is basically a solid disc. For our illustrative purposes we’ll divide this disc into hypothetical parts, each having a mass m located a distance r from the flywheel’s center of rotation. We’ll select a single part to examine and call that A.
Two Types of Velocity Associated With a Spinning Flywheel
Part A has a mass, mA, and is located a distance rA from the flywheel’s center of rotation. As the flywheel spins, part A rides along with it at an angular velocity, ω, following a circular path, shown in green. It also moves at a linear velocity, vA, shown in red. vA represents the linear velocity of part A measured at any point tangent to its circular path. This linear velocity would become evident if part A were to become disengaged from the flywheel and cast into the air, whereupon its trajectory would follow a straight line tangent to its circular path.
The linear and angular velocities of part A are related by the formula,
vA = rA × ω
Next time we’ll use this equation to modify the basic kinetic energy formula so that it’s placed into terms that relate to a flywheel’s angular velocity. This will allow us to define a phenomenon at play in the flywheel’s rotation, known as the moment of inertia.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: angular velocity, energy stored, engineering, flywheel, kinetic energy, linear velocity, mass, moment of inertia, spinning flywheel
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Two Types of Velocity Associated With a Spinning Flywheel
Tuesday, October 10th, 2017
|
Last time we introduced angular velocity with regard to flywheels and how a fixed point riding piggyback on a moving flywheel travels the same circular path as its host at a pace that’s measured in units of degrees per second. Today we’ll introduce another unit of measure, the radian, and see how it’s uniquely used to measure angles of circular motion in units of radians per second.
Radians and the Angular Velocity of a Flywheel
Back in elementary school we worked with protractors and measured angles in degrees, and we were all too familiar with the fact that the average protractor maxed out at 180, or half the degrees present in a complete circle. But in the grownup worlds of physics and engineering, angles of circular motion are measured in units called radians, an international standard equal to 57.3 degrees that’s used to measure objects rotating in circular motion.
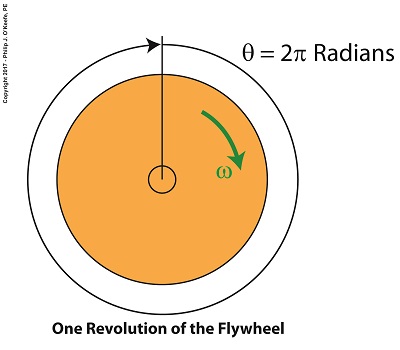
If we divide a circle’s value of 360 degrees by the 57.3 degrees that represent a radian, we find there are 6.28 radians in a circle, and oddly enough, it just so happens that 6.28 is equal to 2 × π. Anyone who stayed awake during math class can’t help but remember that π represents a constant value of 3.14, a number that pops up anytime you divide the circumference of a circle by its diameter. No matter the circle’s size, π will always result when you perform this operation.
Applying these facts to radians, we find that during one complete revolution of a flywheel the measure of the angle θ increases from 0 radians to 2π radians.
Suppose we have a flywheel spinning at N revolutions per minute, or RPMs. To calculate the angular velocity, ω, of any point on the flywheel, or the whole wheel for that matter, we use the following formula which provides an answer in radians per second,
ω = [2 × π × N ] ÷ 60 seconds/minute (1)
If a flywheel spins at 3000 RPM, its angular velocity is calculated as,
ω = [2 × π × (3000 RPM)] ÷ 60 seconds/minute (2)
ω = 314.16 radians/second (3)
Next time we’ll see how angular velocity is used to determine the kinetic energy contained within a flywheel.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: angular velocity, degrees, engineering, flywheel, kinetic energy, radians, revolutions per minute, RPM
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Radians and the Angular Velocity of a Flywheel
Wednesday, October 4th, 2017
|
We introduced the flywheel in our last blog and the fact that as long as it’s spinning it acts as a kinetic energy storage device. Today we’ll work our way towards an understanding of how this happens when we discuss angular velocity.
Angular velocity is represented in engineering and physics by the symbol, ω, the Greek letter Omega. The term angular is used to denote physical quantities measured with respect to an angle, especially those quantities associated with rotation.
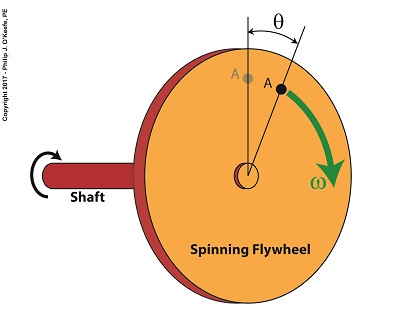
Angular Velocity of a Flywheel
To understand how angular velocity manifests let’s consider a fixed point on the face of a flywheel, represented in the illustration as A. When the flywheel is at rest, point A is in the 12 o’clock position, and as it spins A travels clockwise in a circular path. An angle, θ, is formed as A’s position follows along with the rotation of the flywheel. The angle increases in size as A travels further from its starting point. If A moves one complete revolution, θ will equal 360 degrees, or the total number of degrees present in a circle.
As the flywheel spins through its first revolution into its second, point A travels past its point of origination, and in two complete revolutions it will travel 2 × 360, or 720 degrees, in three revolutions 3 × 360, or 1080 degrees, and so forth. The degrees A travels continue to increase with each revolution of the flywheel.
Angular velocity represents the total number of degrees A travels within a given time period. If we measure the flywheel’s rotational speed with a tachometer and find it takes one second to make 50 revolutions, point A will have traveled the circumference of its path fifty times, and A’s angular velocity would be calculated as,
ω = (50 revolutions per second) × (360 degrees per revolution)
ω = 18,000 degrees per second
Next time we’ll introduce a unit of measurement known as radians which is uniquely used to measuring the angles of circular motion.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: angular velocity, energy storage, engineering, flywheel, kinetic energy
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Angular Velocity of a Flywheel
Monday, September 25th, 2017
|
What came first? The wheel or the flywheel? Archeologists have been debating this question for decades. One thing is certain, they both date back to prehistoric times.

What Came First? The Wheel or the Flywheel?
One of the oldest flywheel discoveries was a potter’s wheel, used to make pottery. It’s a turntable made of stone or heavy wood that’s connected to a massive wheel by a spinning shaft. Once the potter got the flywheel spinning with his hand or foot, the wheel’s heavy weight kept it in virtual perpetual motion, allowing the potter to concentrate on forming the clay he shaped with his hands.
A potter’s wheel, or any other flywheel for that matter, takes a lot of initial effort to put into motion. In other words, the potter must put a lot of his own muscles’ mechanical energy into the flywheel to get it moving. That’s because its sheer weight binds it to the Law of Inertia and makes it want to stay at rest.
But once the flywheel is in motion, the potter’s mechanical energy input is transformed into kinetic energy, the energy of motion. The kinetic energy the potter produces by his efforts results in surplus energy stored within the flywheel. Hence, the flywheel serves as a kinetic energy storage device, similar to a battery which stores electrical energy. As long as the flywheel remains in motion, this stored energy will be used to keep the turntable spinning, which results in no additional mechanical energy needing to be exerted by the potter while forming pots.
The flywheel’s stored energy also makes it hard to stop once it’s in motion. But eventually the frictional force between the potter’s hands and the clay he works drains off all stored kinetic energy.
Since the Industrial Revolution flywheels have been used to store kinetic energy to satisfy energy demands and provide a continuous output of power, which increases mechanical efficiency.
Next time we’ll begin our exploration into the science behind flywheels and see how they’re used in diverse engineering applications.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: energy storage, engineering, flywheel, frictional force, inertia, kinetic energy, mechanical energy
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on What Came First? The Wheel or the Flywheel?
Friday, September 15th, 2017
|
It’s been awhile since we began our discussion of a pulley-belt assembly operating within a hydroponics plant, and we’ve solved for a lot variables and derived many equations along the way. Today we’ll tackle the two remaining variables, T1 , the belt’s tight side tension, and T2 , its loose side tension, and we’ll determine exactly what belt width will optimize power transmission within our system.
Optimizing Belt Width in a Pulley-Belt Assembly
Last time we converted mechanical power, P, from horsepower into foot-pounds per second and the belt’s velocity, V, into feet per second in order to get things into terms we can work with. We then inserted these values into the mechanical power formula to get,
2,200 foot pounds per second = (T1 – T2) × 3.93 feet/second (1)
This equation will allow us to solve for T1 and T2, and from there we’ll develop a value for the optimum belt width.
Previously, we determined from the Euler-Eytelwein Formula that,
T1 = 2.38T2 (2)
Substituting equation (2) into equation (1), we get,
2,200 foot pounds per second = (2.38T2 – T2) × 3.93 feet/second (3)
Reducing this equation with algebra we arrive at,
T2 = 405.65 pounds (4)
We can now insert equation (4) into equation (2) and calculate T1,
T1 = 2.38 × 405.65 pounds (5)
T1 = 965.44 pounds (6)
T1 is maximum tension in the belt, specified by the manufacturer to be 300 pounds per inch of width, which makes the minimum width belt to be used to optimize power transmission within our pulley-belt assembly,
w = T1 ÷ 300 pounds per inch (7)
w = 965.44 pounds ÷ 300 pounds per inch (8)
w = 3.22 inches (9)
We can use a belt of minimum width of 3.22 inches to safely transmit 4 horsepower from the engine to the pump without incurring breakage and slippage along the belt, thereby optimizing power transmission within our assembly. If we used a narrower belt, breaking and slippage would occur. If we used a wider belt, an unnecessary expense would be incurred.
Next time we’ll begin a discussion on flywheels as they apply to rotating machinery like gasoline and steam engines.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, belt width, belt-pulley assembly, loose side tension, maximum tension, mechanical power, optimizing power transmission, pulley, slippage, tight side tension
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Optimizing Belt Width in a Pulley-Belt Assembly
Monday, September 4th, 2017
|
We’ve been working our way towards developing values for variables in our example pulley-belt assembly, and last time we calculated the velocity of the belt in that assembly to be 237.99 feet per minute. But before we can go on to calculate the belt’s loose side tension, T2, and tight side tension, T1, we’ll need to discuss unit conversion, specifically how to convert horsepower into foot-pounds per second.
Our working formula for this demonstration is the formula for mechanical power, P, previously introduced and shown again here,
P = (T1 – T2) × V (1)
By engineering convention mechanical power is normally measured in units of foot-pounds per second. But if you’ll recall from a past blog in which we determined the belt’s velocity, V, it was measured in units of feet per minute, not per second.
To further complicate things, the difference in belt tensions, T1 – T2, is stated in units of pounds, and combining these elements together results in P being expressed in foot-pounds per minute, not the required per second, because we are multiplying feet per minute by pounds. That’s a whole lot of unit changing within a single equation, which makes for an awkward situation.
To smooth things out we’ll have to do some converting of units. We’ll start by dividing V by 60 seconds per minute so it can be expressed in units of feet per second,
V = 237.99 feet per minute ÷ 60 seconds per minute (2)
V = 3.93 feet/second (3)
The power in our belt was previously given as 4 horsepower, which must also undergo conversion and be put in terms of foot-pounds per second so it can be used in equation (1).

Unit Conversion, Horsepower to Foot-Pounds per Second
One horsepower is equal to 550 foot-pounds per second, which makes the amount of power, P, in our pulley-belt assembly equal to 2,200 foot-pounds per second.
Units converted, we can now insert the values for V and P into equation (1) to arrive at,
2,200 foot pounds per second = (T1 – T2) × 3.93 feet/second (4)
Next time we’ll use this relationship to develop values for T1 and T2, the belt’s tight and loose side tensions.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, belt and pulley assembly, belt velocity, engineering, foot pounds per second, horsepower, loose side tension, mechanical power, pulley, tight side tension, unit conversions, units
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Unit Conversion, Horsepower to Foot-Pounds per Second
Monday, August 28th, 2017
|
We’ve been discussing tangential velocity within the context of a pulley and belt assembly in recent blogs, and you may have wondered whether you encounter this phenomenon in your everyday life. Undoubtedly you have. Have you ever driven a long stretch of highway at a fast clip and suddenly come upon a curve in the road posted at a lower speed limit? If you happened not to notice the speed reduction, you may have found yourself slamming on the brakes to regain control of your car. You’ve been caught in a tangential velocity danger zone.

Tangential Velocity Dangers
As this road sign indicates, cyclists must also beware of potentially dangerous circumstances involving tangential velocity. It warns of an upcoming drop in the road, which, depending on their speed, has the potential to catapult them into the air.
Next time we’ll resume our discussion of tangential velocity and other factors within the context of our pulley-belt assembly.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, brakes, danger zone, pulley, pulley and belt assembly, speed, speed limit, tangential velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Tangential Velocity Dangers
Monday, August 21st, 2017
|
Last time we developed an equation to compute tangential velocity, V, of the belt in our example pulley and belt system. Today we’ll plug numbers into this equation and arrive at a numerical value for this belt velocity.
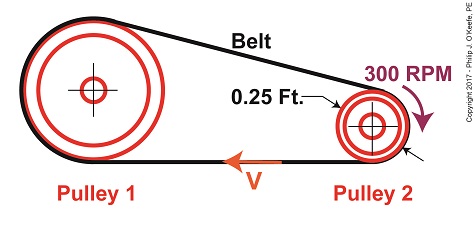
Belt Velocity
The equation we’ll be working with is,
V = π × D2 ÷ t2 (1)
where, D2 is the diameter of Pulley 2 and π represents the constant 3.1416. We learned that Pulley 2’s period of revolution, t2, is related to its rotational speed, N2, which represents the time it takes for it to make one revolution and is represented by this equation,
N2 = 1 ÷ t2 (2)
We’ll now solve for the belt’s velocity, V, using known values, starting off with rearranging terms so we can solve for t2,
t2 = 1 ÷ N2 (3)
We were previously given that N2 is 300 RPM, or revolutions per minute, so equation (3) becomes,
t2 = 1 ÷ 300 RPM = 0.0033 minutes (4)
This tells us that Pulley 2 takes 0.0033 minutes to make one revolution in our pulley-belt assembly.
Pulley 2’s diameter, D2, was previously determined to be 0.25 feet. Inserting this value equation (1) becomes,
V = π × (0.25 feet) ÷ (0.0033 minutes) (5)
V = 237.99 feet/minute (6)
We’ve now determined that the belt in our pulley-belt assembly zips around at a velocity of 237.99 feet per minute.
Next time we’ll apply this value to equation (6) and determine the belt’s tight side tension, T1.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, belt velocity, loose side tension, minimum belt width, period of revolution, pulley, pulley and belt system, pulley diameter, pulley rotational speed, tangential velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Belt Velocity













