Engineering Expert Witness Blog

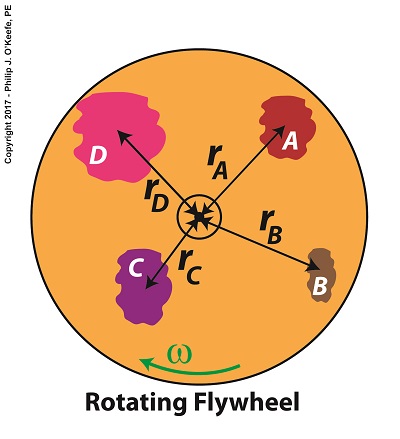
    Last time we introduced the fact that spinning flywheels are subject to both linear and angular velocities, along with a formula that allows us to calculate these quantities for a single part of the flywheel, designated A.   We also re-visited the kinetic energy formula.   Today we’ll build upon those formulas as we attempt to answer the question, How much kinetic energy is contained within a spinning flywheel?

    Here again is the basic kinetic energy formula,

KE = ½ × m × v²                                                                (1)

where, m equals a moving object’s mass and v is its linear velocity.

    Here again is the formula used to calculate linear and angular velocities for a single part A within the flywheel, where part A’s linear velocity is designated v_A,  angular velocity by ω, and where r_A is the distance of part A from the flywheel’s center of rotation.

v_A = r_A × ω                                                                         (2)

    Working with these two formulas, we’ll insert equation (2) into equation (1) to obtain a kinetic energy formula which allows us to calculate the amount of energy contained in part A of the flywheel,

KE_A = ½ × m_A × (r_A × ω)²                                                 (3)

which simplifies to,

KE_A = ½ × m_A ×  r_A²  ×  ω²                                              (4)

    Equation (4) is a great place to begin to calculate the amount of kinetic energy contained within a spinning flywheel, however it is just a beginning, because a flywheel contains many parts.  Each of those parts has its own mass, m, and is a unique distance, r, from the flywheel’s center of rotation, and all these parts must be accounted for in order to arrive at a calculation for the total amount of kinetic energy contained within a spinning flywheel.

How Much Kinetic Energy is Contained Within a Spinning Flywheel?

    Put another way, we must add together all the m × r² terms for each and every part of the entire flywheel.   How many parts are we speaking of?  Well, that depends on the type of flywheel.  We’ll discuss that in detail later, after we define a phenomenon that influences the kinetic energy of a flywheel known as the moment of inertia.

    For now, let’s just consider the flywheel’s parts in general terms.  A general formula to compute the kinetic energy contained within the totality of a spinning flywheel is,

KE = ½ × ∑[m × r²] × ω²                                                  (5)

    We’ll discuss the significance of each of these variables next time when we arrive at a method to calculate the kinetic energy contained within all the many parts of a spinning flywheel

.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________