|
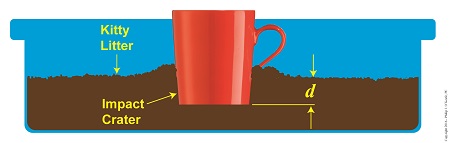
It’s not uncommon in my work as an engineering expert to encounter a situation in which I’m missing information. At that point I’ve got to find a creative solution to working the problem. We’ll get creative today when we combine the Law of Conservation of Energy and the Work-Energy Theorem to get around the fact that we’re missing a key quantity to calculate forces exerted upon the falling coffee mug we’ve been following in this blog series. Last time we applied the Work-Energy Theorem to our mug as it came to rest in a pan of kitty litter. Today we’ll set up the Theorem formula to calculate the force acting upon it when it meets the litter. Here’s where we left off, F × d = –½ × m × v12 where, F is the force acting to slow the progress of the mug with mass m inside the litter pan. The mug eventually stops and comes to rest in a crater with a depth, d. The left side of the equation represents the mug’s work expenditure, as it plows through the litter, which acts as a force acting in opposition to the mug’s travel. Kinetic Energy Meets Up With Displacement
The right side of the equation represents the mug’s kinetic energy, which it gained in freefall, at its point of impact with the litter. The right side is in negative terms because the mug loses energy when it meets up with this opposing force. Let’s say we know the values for variables d and m, quantities which are easily measured. But the kinetic energy side of the equation also features a variable of unknown value, v1, the mug’s velocity upon impact. This quantity is difficult to measure without sophisticated electronic equipment, something along the lines of a radar speed detector used by traffic cops. For the purpose of our discussion we’ll say that we don’t have a cop standing nearby to measure the mug’s falling speed. If you’ll recall from past blog discussions, the Law of Conservation of Energy states that an object’s — in this case our mug’s — kinetic energy is equal to its potential energy. It’s this equivalency relationship which will enable us to solve the equation and work around the fact that we don’t have a value for v1. We’ll do the math and plug in the numbers next time. Copyright 2016 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |