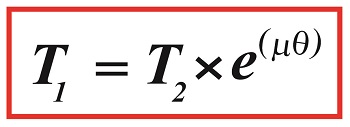|
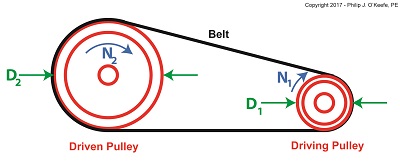
Last time we introduced the Pulley Speed Ratio Formula, a Formula which assumes a certain amount of friction in a pulley-belt assembly in order to work. Today we’ll introduce another Formula, one which oversees how friction comes into play between belts and pulleys, the Euler-Eytelwein Formula. It’s a Formula developed by two pioneers of engineering introduced in an earlier blog, Leonhard Euler and Johann Albert Eytelwein. Here again is the Pulley Speed Ratio Formula, D1 × N1 = D2 × N2 where, D1 is the diameter of the driving pulley and D2 the diameter of the driven pulley. The pulleys’ rotational speeds are represented by N1 and N2. This equation works when it operates under the assumption that friction between the belt and pulleys is, like Goldilock’s preferred bed, “just so.” Meaning, friction present is high enough so the belt doesn’t slip, yet loose enough so as not to bring the performance of a rotating piece of machinery to a grinding halt. Ideally, you want no slippage between belt and pulleys, but the only way for that to happen is if you have perfect friction between their surfaces—something that will never happen because there’s always some degree of slippage. So how do we design a pulley-belt system to maximize friction and minimize slip? Before we get into that, we must first gain an understanding of how friction comes into play between belts and pulleys. To do so we’ll use the famous Euler-Eytelwein Formula, shown here, A First Look at the Euler-Eytelwein Formula
where, T1 and T2 are belt tensions on either side of a pulley. We’ll continue our exploration of the Euler-Eytelwein Formula next time when we discuss the significance of its two sources of tension. Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |