Posts Tagged ‘energy’
Friday, December 18th, 2015
|
My work as an engineering expert sometimes involves computations of energy expended, as when I must determine how much energy is required to move something. But sometimes the opposite needs to be calculated, that is, how much energy is required to stop something already in motion. That’s the subject of today’s discussion, which we’ll approach by way of the Work-Energy Theorem.
The Work-Energy Theorem states that the work required to slow or stop a moving object is equal to the change in energy the object experiences while in motion, that is, how its kinetic energy is reduced or completely exhausted. Although we don’t know who to attribute the Theorem to specifically, we do know it’s based on the previous work of Gaspard Gustave de Coriolis and James Prescott Joule, whose work in turn built upon that of Isaac Newton’s Second Law of Motion.
Consider the example shown here. A ball of mass m moves unimpeded through space at a velocity of v1 until it is met by an opposing force, F. This force acts upon the ball over a travel distance d, resulting in the ball’s slowing to a velocity of v2.
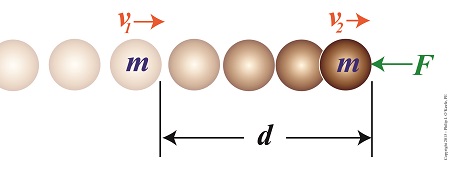
The Work – Energy Theorem Illustrated
Does the illustration make clear the Work-Energy Theorem dynamics at play? If not, return for the second part of this blog, where we’ll clarify things by getting into the math behind the action.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: energy, engineering expert witness, Gaspard-Gustave de Coriolis, Isaac Newton's Second Law of Motion, James Prescott Joule, kinetic energy, moving object, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Work-Energy Theorem — Background
Thursday, December 10th, 2015
|
My work as an engineering expert has often required that I perform calculations to quantify the energy consumed by electric motors and steam turbines, such as when they work together at power plants to generate electricity. Today we’ll see how work and energy share an interesting relationship that is brought out by examining the units by which they are measured.
Last time we used de Coriolis’ formula to compute work to calculate the amount of work performed while pushing a loaded wheelbarrow a distance of 3 meters. We found that in order to move the wheelbarrow that distance, a gardener must exert a force equal to 534 Newton • meters of work. That relationship is shown here,
Work = 178 Newtons × 3 meters = 534 Newton • meters (1)

de Coriolis’ Formula to Compute Work
The Newton, as discussed previously in this blog series, is shorthand notation for metric units of force, and we’ll use those units today to demonstrate the special relationship between work and energy.
We’ll start by supposing that you’re unfamiliar with the Newton as a unit of measurement. In that case you’d have to employ longhand notation to quantify things, which means you’d be measuring units of force in terms of kilogram • meters per second2.
Putting equation (1) in longhand notation terms, we arrive at,
Work = 178 kilogram • meters per second2 × 3 meters (2)
Work = 534 kilogram • meters2 per second2 (3)
If you’ve been following along in this blog series, you’ll recognize that the unit of measurement used to compute work, namely, kilogram • meters2 per second2, is the same as was used previously to measure energy. That unit is the Joule, which is considerably less wordy.
Equations (2) and (3) bear out the interesting relationship between work and energy — they share the same unit of measure. This relationship would not be apparent if we only considered the units for work presented in equation (1).
So following standard engineering convention where work and energy are expressed in the same units, the work required to push the wheelbarrow is expressed as,
Work = 534 Joules
Yes, work and energy are measured by the same unit, the Joule. But, energy isn’t the same as work. Energy is distinguished from work in that it’s the measure of the ability to perform work. Stated another way, work cannot be performed unless there is energy available to do it, just as when you eat it provides more than mere pleasure, it provides your body with the energy required to perform the work of pushing a wheelbarrow through the garden.
Next time we’ll see how work factors into the Work Energy Theorem, which mathematically relates work to energy.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis' formula to compute work, electric motors, energy, engineering expert, generate electricity, joule, Newton meters, Newtons, power plants, steam turbines, unit of energy, units of force, work, work energy relationship, work required
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Work and Energy Share an Interesting Relationship
Sunday, November 29th, 2015
|
Although I’m an engineering expert in the 21st Century, I often have to employ engineering principles that are centuries old. A case in point is Gaspard Gustave de Coriolis‘ formula to compute work, as set out in his Principle of Work. We’ll work with his formula today, and we’ll introduce a unit of measurement used to quantify work known as the Newton.
de Coriolis’ formula to compute work is used to determine the amount of work, that is, the amount of dynamic energy available to influence the movement of an object, and is calculated by the formula,
Work = Force × Distance
where F represents the force acting upon an object that travels a distance of D. Force is most often expressed in metric units as kilogram • meter per second2, a wordy expression which is more conveniently referred to as the Newton.
In the image below, F is the force of 178 Newtons exerted by the gardener to push his filled wheelbarrow a distance of 3 meters. The quantity 178 Newtons was obtained by way of direct personal experience working in my own garden. I’ve found that it takes approximately 40 pounds of force to push a wheelbarrow loaded with dirt across level ground. Because one pound of force is equal to 4.45 Newtons, the amount of force I exerted is expressed as,
[40 pounds of force] × [4.45 Newtons per pound force] = 178 Newtons

Work = Force × Distance
If 178 Newtons of force is required to push the wheelbarrow a distance of 3 meters, then the work performed is expressed as,
Work = 178 Newtons × 3 meters
= 534 Newton • meters
Next time we’ll explore the special relationship between work and energy and introduce another unit used to quantify work.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis' formula to compute work, distance, energy, engineering expert, force, Gaspard Gustave de Coriolis' principle of work, Newton, work formula
Posted in Engineering and Science, Expert Witness, Innovation and Intellectual Property, Personal Injury | Comments Off on de Coriolis’ Formula to Compute Work and the Newton
Wednesday, December 4th, 2013
|
Last time we ran our basic power plant steam turbine without a condenser. In that configuration the steam from the turbine exhaust was simply discharged to the surrounding atmosphere. Today we’ll connect it to a condenser to see how it improves the turbine’s efficiency.
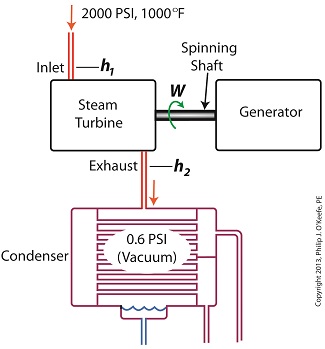
As discussed in a previous blog, enthalpy h1 is solely dependent on the pressure and temperature at the turbine inlet. For purposes of today’s discussion, turbine inlet steam pressure and temperature will remain as last time, with values of 2,000 lbs PSI and 1000°F respectively, and calculations today will be based upon those values. So to review, the inlet enthalpy h1 is,
h1 = 1474 BTU/lb
If the condenser vacuum exists at a pressure of 0.6 PSI, a realistic value for a power plant condenser, then referring to the steam tables in the Van Wylen and Sonntag thermodynamics book, we find that the enthalpy h2 will be,
h2 = 847 BTU/lb
and the amount of useful work that the turbine can perform with the condenser in place would therefore be,
W = h1 – h2 = 1474 BTU/lb – 847 BTU/lb = 627 BTU/lb
So essentially with the condenser present, the work of the turbine is increased by 168 BTU/lb (627 BTU/lb – 459 BTU/lb). To put this increase into terms we can relate to, consider this. Suppose there’s one million pounds of steam flowing through the turbine each hour. Knowing this, the turbine power increase, P, is calculated to be,
P = (168 BTU/lb) ´ (1,000,000 lb/hr) = 168,000,000 BTU/hr
Now according to Marks’ Standard Handbook for Mechanical Engineers, a popular general reference book in mechanical engineering circles, one BTU per hour is equivalent to 0.000393 horsepower, or HP. So converting turbine power, P, to horsepower, HP, we get,
P = (168,000,000 BTU/hr) ´ (0.000393 HP/BTU/hr) = 66,025 HP
A typical automobile has a 120 HP engine, so this equation tells us that the turbine horsepower output was increased a great deal simply by adding a condenser to the turbine exhaust. In fact, it was increased to the tune of the power behind approximately 550 cars!
What all this means is that the stronger the vacuum within the condenser, the greater the difference between h1 and h2 will be. This results in increased turbine efficiency and work output, as evidenced by the greater numeric value for W. Put another way, the turbine’s increased efficiency is a direct result of the condenser’s vacuum forming action and its recapturing of the steam that would otherwise escape from the turbine’s exhaust into the atmosphere.
This wraps up our series on the power plant water-to-steam cycle. Next time we’ll use the power of 3D animation to turn a static 2D image of a centrifugal clutch into a moving portrayal to see how it works.
________________________________________
|
Tags: automobile engine, BTU, BTU/lb, coal power plant, energy, engineering expert witness, enthalpy, forensic engineer, horsepower, mechanical engineer, power, power engineer, power industry expert, power plant efficiency, power plant expert, power plant training instructor, power plant training seminars, steam pressure, steam turbine, steam turbine expert witness, steam water cycle, thermodynamics, vacuum, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability, Professional Malpractice | Comments Off on How Condensers Increase Efficiency Inside Power Plants
Monday, November 18th, 2013
|
Last time we learned how enthalpy is used to measure heat energy contained in the steam inside a power plant. The higher the steam pressure, the higher the enthalpy, and vice versa, and we touched upon the concept of work, or the potential for a useful outcome of a process. Today we’ll see how to get the maximum work out of a steam turbine by attaching a condenser at the point of its exhaust and making the most of the vacuum that exists within its condenser.
Let’s revisit the equation introduced last time, which allows us to determine the amount of useful work output:
W = h1 – h2
Applied to a power plant’s water-to-steam cycle, enthalpy h1 is solely dependent on the pressure and temperature of steam entering the turbine from the boiler and superheater, as contained within the purple dashed line in the diagram below.
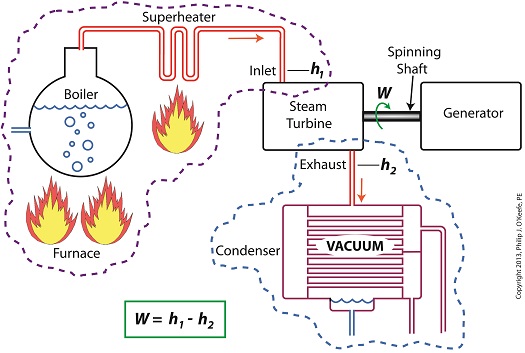
As for enthalpy h2, it’s solely dependent on the pressure and temperature of steam within the condenser portion of the water-to-steam cycle, as shown by the blue dashed circle of the diagram.
Next week we’ll see how the condenser, and more specifically the vacuum inside of it, sets the platform for increased energy production, a/k/a work.
________________________________________
|
Tags: boiler, coal power plant expert witness, condensate, condenser, electric generator, electric utility power plant expert, energy, engineering expert witness, enthalpy, forensic engineering, power engineering expert witness, power plant equipment, power plant training, steam pressure, steam temperature, steam turbine, superheater, turbine exhaust, turbine generator, vacuum, water-to-steam cycle, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Enthalpy and the Potential for More Work
Tuesday, November 5th, 2013
|
Last time we discussed the key functions of the make-up valve in the power plant water-to-steam cycle. Today we’re going to talk about a vacuum. No, not the kind you use around the house, the kind that’s created by the condenser inside a power plant.
As discussed previously, the condenser is a piece of equipment that turns turbine exhaust steam back into water. The water that’s formed during this process is known as condensate, and its density is higher than that of the steam it shares space with inside the condenser. That difference in density is what creates the vacuum inside the condenser vessel. Put another way, the increase in density along with the condenser’s airtight design prevent air from rushing in from outside to occupy any of the space inside the condenser, a desirable condition from an efficiency standpoint.
But to understand how all this works we’ll first have to gain an understanding of what is meant by density. A textbook would define it as the mass of a substance divided by the amount of space that that substance occupies. Let’s take steam and water for example. One pound of steam at 212°F forms a vapor cloud that occupies 26.78 cubic feet of space. If we condensed that pound of steam back into water at the same temperature, it would just about fit into a 16 ounce glass and occupy a mere 0.017 cubic feet.
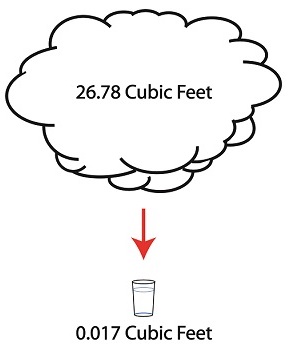
The huge difference in their volumes is due to the fact that steam contains more than five times the heat energy that unheated water does. That energy makes the molecules in a cloud of steam more active, causing them to collide against each other with great force, spread apart, and occupy a larger space.
If you’re wondering what change in density has to do with vacuum in the condenser, allow me to offer an analogy. Ever canned any produce, like tomatoes, in glass jars to over-winter? Not likely, as this once common survival tactic has nearly become a lost art. But the vacuum created inside the condenser is much like the vacuum created within a mason jar during canning.
Inside the glass mason jar, a small space is intentionally left between the tomatoes and lid. During the process of boiling, or heat sterilization, this space fills with steam. Then during cooling the trapped steam condenses into water. This condensation creates the vacuum that sucks down on the jar’s lid, giving it an airtight seal, a condition which won’t allow bacteria to grow on our canned foods. You see, like us bacteria need oxygen to live, but thanks to the vacuum inside our cooked mason jar no air containing oxygen will remain inside to harbor it.
Next time we’ll continue our discussion on vacuum to see how it’s used to increase a steam turbine’s efficiency.
________________________________________
|
Tags: coal power plant, condensate, condenser, density, electrical power, energy, engineering expert witness, forensic engineer, heat energy, make up valve, power engineer, power plant, power plant training, steam and water cycle, steam turbine efficiency, vacuum
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Vacuum in a Power Plant Condenser
Sunday, March 20th, 2011
| Ever take a peek inside the toaster while you’re waiting for the toast to pop up? If so, you would have noticed a bright orange glow. That glow is produced when the toasting wires heat up, which in turn creates a nice crusty surface on your bread or waffle. It’s the same phenomenon as when the filament inside an incandescent bulb glows. The light and heat produced in both these cases are the result of the Joule, pronounced “jewel,” effect at work.
To understand Joule heating, let’s first refresh our memories as to electrical current resistance. We learned previously that wire is not a perfect conductor, and as such resistance to flow is encountered. This resistance causes power to be lost along the length of wire, in accordance with this equation:
Power Loss = I2 × R
Where I is the electric current flowing through a wire, and R is the total electrical resistance of the wire. The power loss is measured in units of Joules per second, otherwise known as watts, “watt” denoting a metric unit of power. It is named after the famed Scottish mechanical engineer, James Watt, who is responsible for inventing the modern steam engine. A Joule is a metric unit of heat energy, named after the English scientist James Prescott Joule. He was a pioneer in the field of thermodynamics, a branch of physics concerned with the relationships between different forms of energy.
Anyway, to see how the equation works, let’s look at an example. Suppose we have 12 feet of 12 AWG copper wire. We are using it to feed power to an appliance that draws 10 amperes of electric current. Going to our handy engineering reference book, we find that the 12 AWG wire has an electrical resistance of 0.001588 ohms per foot, “ohm” being a unit of electrical resistance. Plugging in the numbers, our equation for total electrical resistance becomes:
R = (0.001588 ohms per foot) × 12 feet = 0.01905 ohms
And we can now calculate power loss as follows:
Power = I2 × R = (10 amperes)2 × (0.01905 ohms) = 1.905 watts
Instead of using a 12 AWG wire, let’s use a smaller diameter wire, say, 26 AWG. Our engineering reference book says that 26 AWG wire has an electrical resistance of 0.0418 ohms per foot. So let’s see how this changes the power loss:
R = (0.0418 ohms per foot) × 12 feet = 0.5016 ohms
Power = I2 × R = (10 amperes)2 × (0.5016 ohms) = 50.16 watts
This explains why appliances like space heaters and window unit air conditioners have short, thick power cords. They draw a lot of current when they operate, and a short power cord, precisely because it is short, poses less electrical resistance than a long cord. A thicker cord also helps reduce resistance to power flow. The result is a large amount of current flowing through a superhighway of wire, the wide berth reducing both the amount of power loss and the probability of dangerous Joule heating effect from taking place.
Our example shows that the electric current flowing through the 12 AWG wire loses 1.905 watts of power due to the inconsistencies within the wire, and this in turn causes the wire to heat up. This is Joule heating at work. Joule heating of 50.16 watts in the thinner 26 AWG wire can lead to serious trouble.
When using a power cord, heat moves from the copper wire within it, whose job it is to conduct electricity, and beyond, on to the electrical insulation that surrounds it. There the heat is not trapped, but escapes into the environment surrounding the cord. If the wire has low internal resistance and the amount of current flowing through it is within limits which are deemed to be acceptable, then Joule heating can be safely dissipated and the wire remains cool. But if the current goes beyond the safe limit, as specified in the American Wire Gauge (AWG) table for that type of wire, then overheating can be the result. The electrical insulation may start to melt and burn, and the local fire department may then become involved.
That’s it for wire sizing and electric current. Next time we’ll slip back into the mechanical world and explore a new topic: the principles of ventilation.
_____________________________________________

|
Tags: air conditioner, American Wire Gauge, AWG, current, electrical fire, electrical safety, energy, engineering expert witness, forensic engineer, heat, insulation, Joule heating, overload, physics, power, power cord, power loss, resistance, space heater, steam engine, thermodynamics, Watt
Posted in Engineering and Science | 1 Comment »










