| Ever venture into your basement and stare in amazement at the labyrinth of ductwork stemming off from the furnace? Believe it or not, there’s a science behind that spaghetti bowl configuration. Ductwork can either be flexible or rigid, square or round in shape. Its job in a local exhaust ventilation system is to carry airborne contaminants from the originating source, the carefully positioned hood in the workplace, to the exhaust stack where it is vented outside the building. This job isn’t an easy one. Fluids, like air thick with toxins and toxic gases, don’t want to flow very well through ductwork unless you make their path as unimpeded as possible.
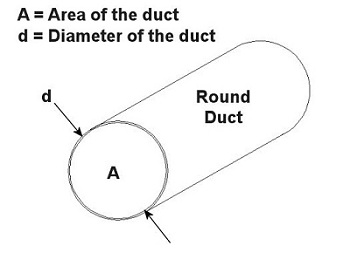
You can think of the air and contaminants flowing through ductwork as if it were like a car moving down a highway. Expressways don’t have sharp 90 degree turns or abrupt changes in width. These would cause a slow down in traffic, unless of course an accident is in the way. Expressways also tend to be rather large thoroughfares. The science behind ductwork follows the same basic principles to work effectively. It will minimize or eliminate sharp turns and it will avoid any abrupt changes in diameter. It will also be as wide in diameter as the environment will accommodate in order to move air volume most effectively. A local exhaust ventilation system’s performance can be greatly hampered and workers exposed to hazards if ductwork leaks. And if the leaks are upstream of the fan and large enough, they can reduce the ability of the local exhaust ventilation system to draw the airborne contaminants into the hood. Air starts getting drawn in through the leaks rather than through the hood. If the leaks are downstream of the fan, the airborne contaminants can re-enter the work area through the leaks rather than going outside through the exhaust stack. Ducts come in an endless variety of diameters, the diameter being part of a simple mathematical equation relating to flow velocity. In the simplest of terms, the flow of air through ductwork is governed by the following equation: Q = V × A where Q is the flow rate of air through the duct in cubic feet per minute (CFM), V is velocity of the air flow in feet per minute, and A is the cross sectional area of the duct in square feet. As an example, suppose you want to design a local exhaust ventilation system with ducts no greater than 5 inches in diameter because of space and clearance limitations. You want to use round ducts for the system because they handle air more efficiently and have no sharp corners where dust can collect. If an industrial hygienist determines that the air is required to flow at a minimum of 800 feet per minute through the duct, what is the airflow rate through the duct? Well, since we are dealing with a round duct, its cross sectional area is that of a circle: A = (π × d2) ÷ 4 where d is the diameter of the inside of the duct as shown in Figure 1 below. Figure 1 – Cross Section of a Round Duct So to use this equation for area, to solve for Q, then we must first convert the duct diameter from inches to feet, which makes our equation look like this: 5 inches ÷ 12 inches per foot = 0.416 feet This gives us a duct cross sectional area of: A = (π × (0.416 feet) 2) ÷ 4 = 0.136 square feet And the air will flow through the duct at this rate: Q = V × A = 800 ft./minute × 0.136 ft.2 = 108.8 CFM This air flow rate is good to know, because it will help the designer to select an appropriate fan for the local exhaust ventilation system. This is because fans are listed in manufacturers’ catalogs according to how many CFM they can handle. Next time, we’ll learn more about the rest of the local exhaust ventilation system, namely, the filter, fan, and exhaust stack. _____________________________________________ |
Posts Tagged ‘fluid dynamics’
Industrial Ventilation – Local Exhaust Ventilation Ductwork
Monday, April 25th, 2011Fluid Mechanics in Mechanical Engineering, Part V, Fluid Dynamics Continued
Sunday, February 7th, 2010|
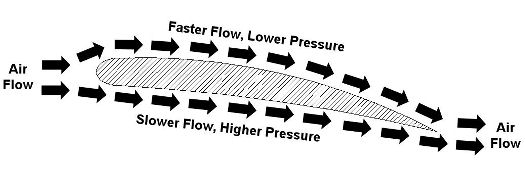
Last week we talked about Daniel Bernoulli and his famous Bernoulli Principle, which is the cornerstone of fluid dynamics. As we’ll see in this week’s installment, the Bernoulli Principle doesn’t just apply to water flowing inside pipes. Let’s consider another instance in which it is instrumental, that of an airplane wing. Figure 1 shows the side view of a wing with arrows indicating direction of air flow as the plane moves through the air. Figure 1 – A Side View of an Airplane Wing
Even though he lived more than 100 years before the first airplane, Bernoulli’s Principle can be used to explain why such a contraption can fly. You see, when comparing air flowing above and beneath a wing, its very shape makes the air flow want to travel faster along the top than it does on the bottom. Bernoulli’s principle comes into play with the airplane wing just as it did in last week’s water pipe flow example. That is, the total energy of flow is the same at all points as the air flows above and below the wing. Now, if air flow speeds up on top of the wing, then the flow’s kinetic energy increases along with it. And remember last week’s analogy of change for $100? Well, something has to give, so in this example the increase in kinetic energy is accomplished at the expense of pressure energy, but the total energy remains the same. This decrease in pressure energy then translates into a drop in pressure on top of the wing. The higher pressure beneath the wing overcomes the lower pressure above the wing. This imbalance is what provides the plane’s lift, enabling it to get off the ground once it achieves a high enough speed on its race down the runway. The Wright brothers, men ahead of their time, were actually among the first aeronautical engineers. They possessed remarkably advanced knowledge of mathematics and mechanical engineering principles. They also understood what Bernoulli taught, and they used his Principle to design and test the shapes of wings on their gliders and planes. They met with success when they determined that the wing’s shape was crucial to supplying lift. In fact, they determined that, depending on the wing’s shape, it would provide the plane with the most lift for the least amount of air speed, allowing them to use a lighter engine to drive the propellers. Weight is always a factor when flying, and the ability to use a lighter engine went a long way towards getting their first plane off the ground. That’s it for Fluid Mechanics. Next week we’ll continue with a discussion of heat transfer, which is the study of how heat moves through vacuums, gases, liquids, and solid objects. _________________________________________________________________ |
Fluid Mechanics in Mechanical Engineering, Part IV, Fluid Dynamics Continued
Sunday, January 31st, 2010|
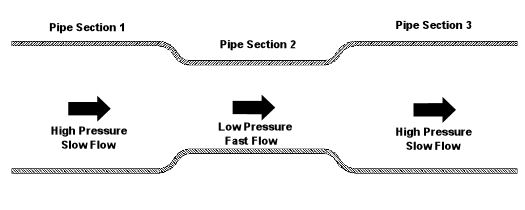
Last week we began our discussion on fluid dynamics. We saw how it’s used to determine flow and velocity of water within a pipe. This week we’ll continue our discussion, exploring in some detail the Bernoulli Principle and what it has to say on the subject. Daniel Bernoulli was a Dutch born mathematician who studied fluid dynamics during the 18th Century. He analyzed the flow of water and determined that as fluid flow speeds up, its pressure goes down, and vice versa. In 1738, he came up with what is now known as the Bernoulli Principle. This Principle is based on the First Law of Thermodynamics, which you will remember teaches us that energy cannot be created or destroyed. One of the conclusions that can be drawn from the Bernoulli Principle is that for fluid flowing steadily, say water within a pipe, or even air flowing over a pitcher’s curve ball in flight, the total energy of the flow remains constant. By “total energy,” I mean the sum of three types of energy: pressure energy, kinetic energy, and potential energy. Total energy will remain constant all along the flow, although its three parts can change. The “pressure energy” part of the total energy is due to the pressure of the fluid flow. For example, pressure energy can be added by a pump to make water flow through a pipe more readily. The “kinetic energy” part of total energy is due to the speed of the fluid flow. And as its name implies, kinetic energy is the energy of movement. The “potential energy” part of the total energy is related to a change in elevation from one end of the fluid flow to the other, like you’d have on a pipe running downhill. It can be said that water at the top of the hill has high potential energy because gravity wants to make it flow down to the bottom of the hill. So how does this Principle help us today? Well, Bernoulli’s Principle is the very foundation upon which fluid dynamics is built, and it’s consistently used to solve complex problems involving fluid flow. To illustrate Bernoulli’s Principle, let’s take a look at Figure l. Here water is flowing through a level pipe with three sections: Figure 1 – Water Flowing Through a Pipe With Three Sections
According to Bernoulli, the total energy of the flowing water is the same from one end of the pipe to the other, and the total energy is equal in each of the three sections of pipe. As the water flows through the pipe from Section 1 to the narrower Section 2, it speeds up as it squeezes through, so its kinetic energy increases. Since the total energy must remain the same and the pipe is level, (this is significant because it means that potential energy is zero), the kinetic energy increases at the expense of pressure energy. This results in a pressure drop in Section 2. Not following? Well, it’s like making change for a hundred dollar bill. Let’s say pressure energy is represented by $20 bills and kinetic energy is represented by $10 bills. Let’s also say that you have $100 worth of these bills in your wallet. The $100 represents the total energy. Now, pretend that you are water flowing into Section 1 of the pipe. While in Section 1, you look in your wallet and you find that you have four $20 bills and two $10 bills, which add up to $100. Okay. Now, when you move into Section 2, you check your wallet again. You discover that your wallet now has three $20 bills and four $10 bills. So you now have fewer $20 bills, more $10 bills, but you still have a total of $100. Fewer $20 bills means lower pressure, and more $10 bills means higher speed. Okay, getting back to the water, what do you think is going to happen when it flows from narrow Section 2 into wide Section 3? Well, the flow will slow down as it fills the extra space present in Section 3. Since the Bernoulli Principle tells us that the total energy of the flow must remain the same, the pressure energy must increase at the expense of the kinetic energy. This in turn causes the pressure within the pipe to go up and the flow’s speed to go down. Thanks to Bernoulli, if we can calculate the total energy in one section of the pipe, then we can calculate the speed of the water flow in another section if the pressure within that section is known. Again, this is possible because we know that the total energy must remain constant all along the flow. Next week we’ll see how the Bernoulli Principle applies to the other type of fluid, air. _________________________________________________________________ |
Fluid Mechanics in Mechanical Engineering, Part III, Fluid Dynamics
Sunday, January 24th, 2010|
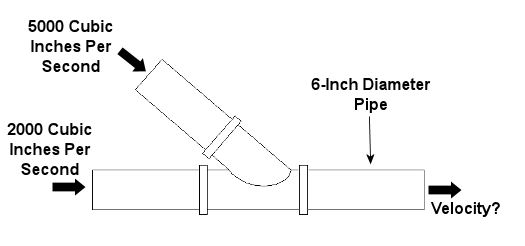
Last week, we learned about some general properties of fluids, concentrating on fluid statics, which is concerned with fluids that don’t move. This week we’ll consider a more dynamic situation, one in which the fluids do move. Remember how we talked about incompressible fluids in the first part of this series on fluid mechanics? We learned that an incompressible fluid, like the oil in a hydraulic jack, can’t be squeezed down into a smaller volume under pressure, so its volume will always remain the same. The same thing goes for other incompressible fluids, like water. By the same token, when water flows through a length of pipe, its volumetric flow rate will remain the same from beginning to end.. By “volumetric flow rate,” I mean the volume of water flowing through the pipe in a given amount of time. It’s measured in cubic inches per second (in3/sec). Now let’s revisit our discussion on the stoichiometry segment of our series on thermodynamics. It’s there that we learned that mass cannot be created or destroyed, and this concept is known as the “conservation of mass.” Applying this principle to incompressible fluids with mass, like water, we can essentially expand on that to say that volume, like mass, can’t be created or destroyed. Because of this, the volumetric flow rate entering the pipe has to equal the flow rate exiting, regardless of whether the pipe diameter changes and whether there are multiple inlets and outlets on the pipe. This volumetric flow rate is related to the velocity, or speed, of water flowing through a round pipe, as well as the interior diameter of the pipe, and it is calculated by this equation: Volumetric Flow Rate = V = (v) x (πd2/4) where “V” is the velocity of the water flowing through the pipe and “d” is the inside diameter of the pipe. The “πd2/4” part of the equation is the cross sectional area of the round pipe. This is derived from the formula used to measure the area of a circle, where the circle’s diameter is “d.” The volumetric flow rate equation above is very useful for designing piping systems used to move of fluids like water from one place to the other. For example, the equation can be used to design the piping system of a municipal water treatment plant. Waste water in, clean water out. Now let’s look at an example. Let’s consider water flowing into the pipe shown in Figure 1 below. If we know the volumetric flow rates of the water going into the two branches, then what would be the velocity of the water coming out?
Figure 1 – A Pipe With Water Flowing Through It
For this problem, let’s use the concept of conservation of volume discussed above and combine it with our volumetric flow rate equation. Applying algebra, we can use the information we are given in Figure 1 to find the solution: Volumetric Flow Rate Going In = Volumetric Flow Rate Going Out VGoing In = VGoing Out VGoing In = [(v) x (πd2/4)]Going Out (VGoing In) / (πd2/4) = vGoing Out vGoing Out = (5000 in3/sec + 2000 in3/sec) / ((π) x (6 in)2/4) = 247.6 in/sec So the water would come shooting out of the pipe at a speed of 247.6 inches per second. That’s pretty fast! Next week we’ll continue with our series on fluid mechanics and explore the Bernoulli principle. By doing so, we’ll examine what’s behind the function of airplane wings and how they enable planes to fly. _________________________________________________________________ |