|
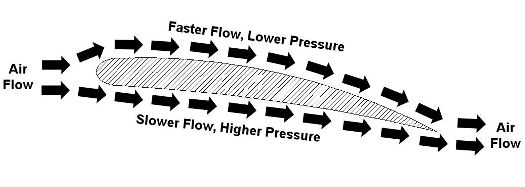
Last week we talked about Daniel Bernoulli and his famous Bernoulli Principle, which is the cornerstone of fluid dynamics. As we’ll see in this week’s installment, the Bernoulli Principle doesn’t just apply to water flowing inside pipes. Let’s consider another instance in which it is instrumental, that of an airplane wing. Figure 1 shows the side view of a wing with arrows indicating direction of air flow as the plane moves through the air. Figure 1 – A Side View of an Airplane Wing
Even though he lived more than 100 years before the first airplane, Bernoulli’s Principle can be used to explain why such a contraption can fly. You see, when comparing air flowing above and beneath a wing, its very shape makes the air flow want to travel faster along the top than it does on the bottom. Bernoulli’s principle comes into play with the airplane wing just as it did in last week’s water pipe flow example. That is, the total energy of flow is the same at all points as the air flows above and below the wing. Now, if air flow speeds up on top of the wing, then the flow’s kinetic energy increases along with it. And remember last week’s analogy of change for $100? Well, something has to give, so in this example the increase in kinetic energy is accomplished at the expense of pressure energy, but the total energy remains the same. This decrease in pressure energy then translates into a drop in pressure on top of the wing. The higher pressure beneath the wing overcomes the lower pressure above the wing. This imbalance is what provides the plane’s lift, enabling it to get off the ground once it achieves a high enough speed on its race down the runway. The Wright brothers, men ahead of their time, were actually among the first aeronautical engineers. They possessed remarkably advanced knowledge of mathematics and mechanical engineering principles. They also understood what Bernoulli taught, and they used his Principle to design and test the shapes of wings on their gliders and planes. They met with success when they determined that the wing’s shape was crucial to supplying lift. In fact, they determined that, depending on the wing’s shape, it would provide the plane with the most lift for the least amount of air speed, allowing them to use a lighter engine to drive the propellers. Weight is always a factor when flying, and the ability to use a lighter engine went a long way towards getting their first plane off the ground. That’s it for Fluid Mechanics. Next week we’ll continue with a discussion of heat transfer, which is the study of how heat moves through vacuums, gases, liquids, and solid objects. _________________________________________________________________ |
Posts Tagged ‘fluid flow’
Fluid Mechanics in Mechanical Engineering, Part V, Fluid Dynamics Continued
Sunday, February 7th, 2010Fluid Mechanics in Mechanical Engineering, Part IV, Fluid Dynamics Continued
Sunday, January 31st, 2010|
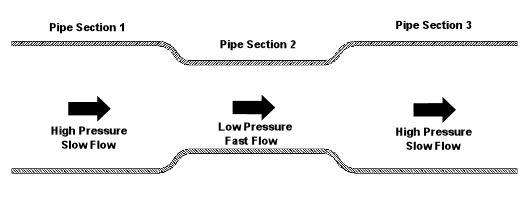
Last week we began our discussion on fluid dynamics. We saw how it’s used to determine flow and velocity of water within a pipe. This week we’ll continue our discussion, exploring in some detail the Bernoulli Principle and what it has to say on the subject. Daniel Bernoulli was a Dutch born mathematician who studied fluid dynamics during the 18th Century. He analyzed the flow of water and determined that as fluid flow speeds up, its pressure goes down, and vice versa. In 1738, he came up with what is now known as the Bernoulli Principle. This Principle is based on the First Law of Thermodynamics, which you will remember teaches us that energy cannot be created or destroyed. One of the conclusions that can be drawn from the Bernoulli Principle is that for fluid flowing steadily, say water within a pipe, or even air flowing over a pitcher’s curve ball in flight, the total energy of the flow remains constant. By “total energy,” I mean the sum of three types of energy: pressure energy, kinetic energy, and potential energy. Total energy will remain constant all along the flow, although its three parts can change. The “pressure energy” part of the total energy is due to the pressure of the fluid flow. For example, pressure energy can be added by a pump to make water flow through a pipe more readily. The “kinetic energy” part of total energy is due to the speed of the fluid flow. And as its name implies, kinetic energy is the energy of movement. The “potential energy” part of the total energy is related to a change in elevation from one end of the fluid flow to the other, like you’d have on a pipe running downhill. It can be said that water at the top of the hill has high potential energy because gravity wants to make it flow down to the bottom of the hill. So how does this Principle help us today? Well, Bernoulli’s Principle is the very foundation upon which fluid dynamics is built, and it’s consistently used to solve complex problems involving fluid flow. To illustrate Bernoulli’s Principle, let’s take a look at Figure l. Here water is flowing through a level pipe with three sections: Figure 1 – Water Flowing Through a Pipe With Three Sections
According to Bernoulli, the total energy of the flowing water is the same from one end of the pipe to the other, and the total energy is equal in each of the three sections of pipe. As the water flows through the pipe from Section 1 to the narrower Section 2, it speeds up as it squeezes through, so its kinetic energy increases. Since the total energy must remain the same and the pipe is level, (this is significant because it means that potential energy is zero), the kinetic energy increases at the expense of pressure energy. This results in a pressure drop in Section 2. Not following? Well, it’s like making change for a hundred dollar bill. Let’s say pressure energy is represented by $20 bills and kinetic energy is represented by $10 bills. Let’s also say that you have $100 worth of these bills in your wallet. The $100 represents the total energy. Now, pretend that you are water flowing into Section 1 of the pipe. While in Section 1, you look in your wallet and you find that you have four $20 bills and two $10 bills, which add up to $100. Okay. Now, when you move into Section 2, you check your wallet again. You discover that your wallet now has three $20 bills and four $10 bills. So you now have fewer $20 bills, more $10 bills, but you still have a total of $100. Fewer $20 bills means lower pressure, and more $10 bills means higher speed. Okay, getting back to the water, what do you think is going to happen when it flows from narrow Section 2 into wide Section 3? Well, the flow will slow down as it fills the extra space present in Section 3. Since the Bernoulli Principle tells us that the total energy of the flow must remain the same, the pressure energy must increase at the expense of the kinetic energy. This in turn causes the pressure within the pipe to go up and the flow’s speed to go down. Thanks to Bernoulli, if we can calculate the total energy in one section of the pipe, then we can calculate the speed of the water flow in another section if the pressure within that section is known. Again, this is possible because we know that the total energy must remain constant all along the flow. Next week we’ll see how the Bernoulli Principle applies to the other type of fluid, air. _________________________________________________________________ |