|
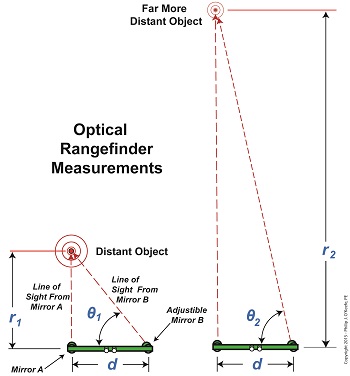
Imagine working, working, working towards a goal and getting oh so close, but never being able to actually reach it. It’s happened to all of us some of the time, but with vertical asymptotes it happens all of the time. We’ll see why the nature of vertical asymptotes presents a problem when measuring extreme distances in today’s blog. We’ve found that optical rangefinders can be useful in measuring long distances. They work well in many situations, but not all. When it comes to extremely long distances they aren’t at all helpful. That’s due to problems presented by trigonometry, more specifically the tangent function and how it leads to vertical asymptotes. Let’s look at Figure 1 to bear this out. Figure 1
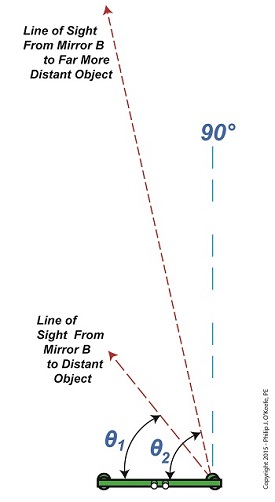
In Figure 1 we see the same rangefinder being used to view objects at two different distances, one distance far greater than the other. There’s an obvious difference in the lengths of the sides of the triangles formed, as well as an obvious difference in angles θ1 and θ2. θ2 is much steeper than θ1. This is more apparent when the lines of sight are isolated, as shown in Figure 2. Figure 2
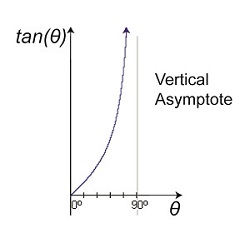
Figure 2 shows that as an object becomes more distant and r, the distance to the object viewed increases, the angle θ gets closer and closer to a value of 90°. What’s significant about this is that a θ value of 90° is impossible for a rangefinder to work with. Why? Because it uses trigonometry to measure distances, more specifically the tangent function within trigonometry, and when θ takes on a value of 90°, it becomes asymptotic in nature — a situation which renders the optical rangefinder useless. To visualize this, we’ve plotted the tangent function for an array of angle θ values on a graph in Figure 3. Figure 3
The curved line represents plotted tangent values for θ that fall between 0° and 90°. What it demonstrates is that as θ gets closer to becoming 90°, it becomes more vertical and steeper in incline. In other words, it forms a vertical asymptote, stretching to reach a value of 90° but never actually getting there. In the math world this means that the tangent’s value is on its way to becoming unbounded or undefined. In plain English this means that the tangent’s value becomes increasingly more unworkable. In fact, the tangent of 90° degrees does not exist. Try entering the number 90 into your calculator and pressing the TAN button. You’ll receive an error message in return. Next week we’ll see the impact this has on the function of an optical rangefinder when the object viewed is so far away the angle θ approaches a value of 90°.
____________________________________
|
Posts Tagged ‘forensic engineer’
Tangent and the Vertical Asymptote
Monday, March 2nd, 2015How An Optical Rangefinder Uses Trigonometry
Monday, February 23rd, 2015|
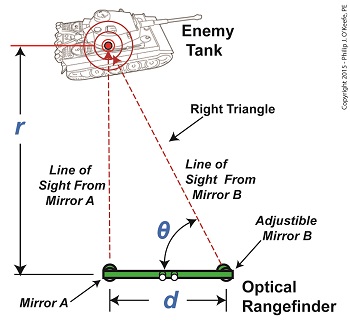
We left off with an artillery soldier spotting an enemy tank in the distance. Luckily, he’s got an optical rangefinder at his disposal to measure the distance between them and crank out an accurate shot. His first action is to peer through the rangefinder’s eyepieces, rotating the adjustable mirror on the right eyepiece until the tank comes into focus. The two lines of sight provided by the left and right eyepieces of the rangefinder form a right triangle due to the parallax effect. One of the angles in this triangle is designated on the illustration by the angle θ, and that’s the angle we’ll be working with. The fact that a right triangle exists means the distance, r, to the tank can be easily measured using principles found in trigonometry, a branch of mathematics that addresses the properties of triangles, hence, the prefix tri in its name. Tangent, and other trigonometric functions like sine and cosine, relate the angles of a right triangle to the ratios of the lengths of the sides of the triangle. In our case we’re concerned with the tangent, which is simply the value that’s derived by dividing the length of the side opposite to the angle θ by the length of its adjacent side. This value can be found in most trigonometry textbook tables, but is most easily found by using a calculator. Simply enter the angle θ‘s value, then press the TAN button. So how does the artillery soldier determine θ‘s value? With the tank in clear focus, it’s easily measured with an indicator gauge attached to the adjustable mirror near the right eyepiece on an optical rangefinder. Our soldier reads the gauge and determines that θ is equal to 89.935°, so the tangent of θ is equal to: tan(θ) = tan(89.935°) = 881.473 Now that we’ve determined the values for d and the tangent of the angle θ, we can plug those numbers into our equation to determine r, the distance to the enemy tank using the equation, r = d × tan(θ) Plugging in numerical values, the equation becomes, r = 3 feet × 881.473 = 2644.419 feet The distance to the tank is 2644.419 feet. Next time we’ll see how the peculiarities of the tangent function place limitations on the accuracy of optical rangefinders over extremely long distances. ____________________________________
|
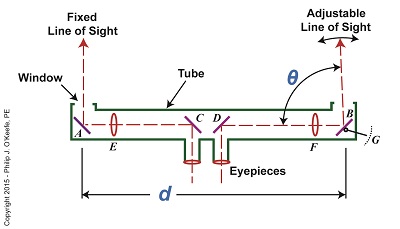
What’s Inside an Optical Rangefinder
Friday, February 13th, 2015|
Last time we covered the mirrors found inside an optical rangefinder. Today we’ll discuss its other components, magnifying lenses E and F and the indicator gauge, G. See Figure 1. Figure 1 Magnifying lenses E and F are positioned in such a way that the two horizontal lines of sight reflecting off mirrors C and D pass through them on their way to mirrors A and B. Lenses E and F are adjustable, allowing the viewer to manipulate them until the distant image being viewed is seen in clear focus through both eyepieces, just as would happen with binoculars. To see the rangefinder in action let’s go out to the battlefield, where it’s routinely used. A soldier notices an enemy tank off in the distance. To make an accurate hit with his artillery he must determine the distance r from his position to the tank. The soldier in charge of this task observes the tank through the rangefinder’s eyepieces and manually adjusts lenses E and F until it comes into focus. He then adjusts the rangefinder’s mirror B until the line of sight extending from it converges on the tank along with the fixed line of sight from mirror A as shown in Figure 2. When the two images converge a right triangle is formed, and as we learned in a previous article, this fact will enable us to calculate r by using trigonometry with this formula: r = d × tan(θ) We already know that the value of d, the distance between mirrors A and B, is three feet. All that is left to be determined is the angle θ that’s formed between adjustable mirror B‘s forward line of sight out the tube’s opening and the horizontal line of sight between D and B. The last component within an optical rangefinder to be discussed is the indicator gauge, notated as G in Figure 1. This gauge is attached to mirror B inside the tube and is used to measure the angle θ that’s produced as the mirror is adjusted. When the lines of sight from mirrors A and B converge and the tank comes into clear view through the eyepieces, the value of θ can be read on the gauge’s numerical graduated scale, which is located on the exterior of the tube. Next time we’ll see how trigonometry and the study of right triangles prove indispensable when measuring distances with an optical rangefinder. ____________________________________
|
Parallax and Trigonometry
Monday, January 26th, 2015|
We’ve been working on a way to calculate the distance to a tree situated blocks from our viewing point. Flying raptors, such as our beloved bald eagle, wouldn’t find this in the least bit challenging. They’re able to accurately judge distances due to their special shape-shifting eye lenses which are capable of actually changing curvature spontaneously. But human physiology isn’t equipped for this task, so we’ll have to employ other methods. Today we’ll see how a branch of mathematics known as trigonometry comes into play. Referring to the illustration, we’d like to calculate the distance, r. You’ll note that a right triangle is formed by Line of Sight A, Path AB, and Line of Sight B. As mentioned in our last blog, right triangles are special because the relationship that exists between their sides and their internal angles is well defined within mathematics. In fact, we can calculate r by using this trigonometric formula, r = d × tan(θ) where d is the length of Path AB, θ is the angle between Line of Sight B and Path AB, and tan(θ) is the trigonometric function known as the tangent. Tangent, and other trigonometric functions like sine and cosine, relate the angles in a right triangle to the ratios of the lengths of the sides of the triangle. If we know two of the variables present in the equation presented above, we can determine the third, and the fact that there’s a right triangle present makes that task so much easier. As things stand now we have two unknowns, d and θ. As pointed out last week, the distance, d, is short, so we’ll use a tape measure to determine its length. Let’s say it measures out to be three feet. Now we need to solve for the angle θ that’s formed between Path AB and Line of Sight B. That’s a bit more challenging. There are a number of devices that can be used to measure θ, including a handheld magnetic compass. However, using a compass often yields inaccurate results, thereby increasing the likelihood of mistakes. A more accurate device to use would be an optical rangefinder, as shown below. The optical rangefinder is a device that’s often used in the military to measure long distances by using the principle of parallax. It functions much like binoculars do, but with a twist, literally, as we’ll see next time. ____________________________________
|
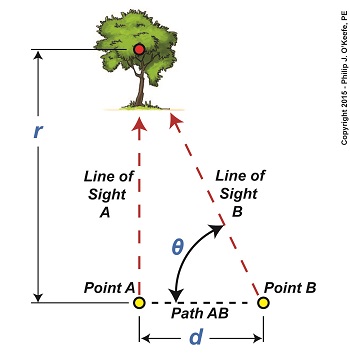
Using Parallax to Measure Distance
Monday, January 19th, 2015|
Last time we introduced an optical effect known as the principle of parallax. Today we’ll get a step closer to seeing how it’s instrumental in measuring distances. For our example we’ll be viewing a point on a tree several blocks away. Since we can’t measure the distance, r, to the tree directly by using a tape measure, we’ll have to use another approach that is made available to us through the principle of parallax. The first step to doing this is to establish two different lines of sight to the red dot on the tree. For our example these will originate at Points A and B, which are both viewing the same spot. Line of Sight A extends straight from Point A to the red spot, while Point B, which is situated only a few feet to the right of A, will provide us with a slanted line of sight to it. We’ll refer to the path between Points A and B as Path AB, which is represented by a black dashed line and has a length, d. You may have noticed from the illustration that Line of Sight B, because it lies on a slant relative to Line of Sight A, provides us with an internal angle, θ, relative to Path AB. This relationship is in fact required to exist if we are to use the principle of parallax, and you’ll see why later. Another requirement is that Path AB must be at a right angle to Line of Sight A, which it is. The illustration bears this out by the fact that a right triangle is formed when Lines of Sight A, B, and Path AB intersect. Right triangles are generally regarded as special within mathematics, but they are particularly special when applying the principle of parallax. The presence of a right triangle enables us to use a branch of mathematics known as trigonometry to correlate the triangle’s angles to the ratios of the lengths of its sides. In other words, we can calculate r by using trigonometry if we are able to measure d and θ. We’ll see how that calculation is done next time. ____________________________________
|
The Principle of Parallax
Thursday, January 8th, 2015|
We’ve been looking at the indirect methods employed by scientists through the ages as they struggled to determine the distance of our Earth from its sun. Today we’ll take a look at one of those indirect methods, known in scientific circles as the Principle of Parallax. Parallax is an optical effect which results in a three dimensional view of the world as seen through our eyes. Because our eyes are spaced a distance apart from each other on the relatively flat surface of our face, each of them will perceive an object along a different line of sight and thus offer differing perspectives. Our brain makes use of the parallax phenomenon to automatically process these differing perspectives into a single image, along with providing us with a three dimensional view of the object, something that comes in handy when negotiating our physical world. As an example, let’s say you’re sitting at the kitchen table staring at a cup of coffee. Your left eye sees the cup from one perspective, your right eye another. To prove it, cover each of your eyes in turn as you look at it. You’ll see that the perspective changes between your two eyes. These two perspectives are processed by your brain into an internal calculation which enables you to adjust your muscle response accordingly. The result is that you are able to deftly pick up the cup of coffee and bring it to your lips rather than clumsily toss it to the floor. Parallax is at work when viewing objects both near and far. Consider Figure 1. Suppose we want to measure the distance from Point A to a tree several blocks away. That’s too far away to use a tape measure, but we can employ the parallax phenomenon and trigonometry, the study of angles, to easily determine the distance. We’ll get a step closer to doing that next time.
____________________________________
|
Kepler’s Third Law Of Planetary Motion
Wednesday, December 31st, 2014|
Edmund Halley was faced with a real puzzle when he began his quest to determine the distance of Earth from the sun. One of the pieces to solving that puzzle came from the work of a German mathematician, astronomer and astrologer named Johannes Kepler. Early in the 17th Century, Kepler spent a lot of time observing the planets in our solar system as they orbited the sun. He discovered that by taking note of the time it took for a planet to make one orbit around the sun, he could determine its relative distance from it. He then compared his findings with other planets, noting the time it took for each to make this same journey. His discovery would come to be known as Kepler’s Third Law of Planetary Motion. But what exactly is meant by a planet’s “relative distance from the sun”? In essence, it means that interplanetary distances, like just about everything else, are relative. Put another way, heavenly bodies can be said to be a distance X relative to another heavenly body if you establish a value for X, whether it’s numerical or otherwise. In Kepler’s case, X would be the unknown value of a so-called astronomical unit (AU), where one AU is equal to the unknown distance from Earth to the sun. Represented in equation form, this distance is: rEarth-sun = 1 AU This relative marker of distance could then be used to show how far the other planets are from the sun, relative to Earth’s distance from the sun, the AU. Kepler’s astronomical unit is simply a placeholder term for an unknown quantity, similar to any other unknown variable that might be used in an algebraic equation. For example, Kepler observed the orbits of Venus and Mars and determined their relative distances to the sun to be: rVenus-sun = 0.72 × 1 AU = 0.72 AU rMars-sun = 1.5 × 1 AU = 1.5 AU In other words, Venus’ distance from the sun is just under three quarters of Earth’s and Mars is one and a half times Earth’s distance from the sun. In this way, Kepler was able to determine the relative distances from the sun in AU for all the observable planets in our solar system. Kepler felt sure that one day scientists would be able to accurately measure Earth’s distance from the sun, and when they accomplished this they could employ his astronomical unit system to determine distances between other planets in our solar system and the sun. Next time we’ll introduce the principle of parallax and see how Halley used this optical effect to devise a method for assigning a value to Kepler’s unknown AU. ____________________________________ |
Gravity and the Mass of the Sun
Friday, December 12th, 2014|
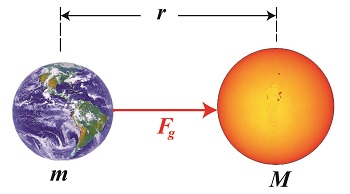
As a young school boy I found it hard to believe that scientists were able to compute the mass of our sun. After all, a galactic-sized measuring device does not exist. But where there’s a will, there’s a way, and by the 18th Century scientists had it all figured out, thanks to the work of others before them. Newton’s two formulas concerning gravity were key to later scientific discoveries, and we’ll be working with them again today to derive a third formula, bringing us a step closer to determining our sun’s mass. Newton’s Second Law of Motion allows us to compute the force of gravity, Fg, acting upon the Earth, which has a mass of m. It is, Fg = m × g (1) Newton’s Universal Law of Gravitation allows us to solve for g, the sun’s acceleration of gravity value, g = (G × M) ÷ r2 (2) where, M is the mass of the sun, r is the distance between the sun and Earth, and G is the universal gravitational constant. You will note that g is a common factor between the two equations, and we’ll use that fact to combine them. We’ll do so by substituting the right side of equation (2) for the g in equation (1) to get, Fg = m × [(G × M) ÷ r2] then, using algebra to rearrange terms, we’ll set up the combined equation to solve for M, the sun’s mass: M = (Fg × r2) ÷ (m × G) (3) At this point in the process we know some values for factors in equation (3), but not others. Thanks to Henry Cavendish’s work we know the value of m, the Earth’s mass, and G, the universal gravitational constant. What we don’t yet know is Earth’s distance to the sun, r, and the gravitational attractive force, Fg, that exists between them. Next time we’ll introduce some key scientists whose work contributed to a method for computing the distance of our planet Earth to its sun. _______________________________________
|
The Inverse Relationship of the Acceleration of Gravity
Friday, December 5th, 2014|
In this blog series we’ve been working our way towards determining mass values for heavenly bodies in our universe. Today we’ll explore the inverse relationship phenomenon that’s present when examining the acceleration of gravity between two heavenly bodies, for our purposes Earth and its moon. To demonstrate the inverse relationship phenomenon, we’ll use Newton’s Law of Gravitation formula: g = (G × M) ÷ r2 (1) In this formula g represents Earth’s acceleration of gravity that’s acting upon the moon. The center of the moon is located at a distance r from Earth’s center. Earth’s mass is represented by M, and G is the universal gravitational constant, which never varies from its value of 3.49 × 10-8 cubic feet per slug per second squared. We’ll solve for Earth’s g factor relative to the moon, which we’ll position at varying distances from Earth’s core, thereby demonstrating how the attracting force of Earth’s gravity becomes weaker as the moon’s distance from Earth’s core increases — hence the inverse relationship. To begin, we know that the present distance from Earth’s center to the center of the moon is about 238,900 miles, or 1,261,392,000 feet. We also know that Earth’s mass, M, is equal to 4.09 × 1023 slugs. Plugging these values into Newton’s Law of Gravitation equation, we calculate the acceleration of gravity exerted upon the moon in this, its normal orbit, to be: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (1,261,392,000 ft)2 g = 0.0089 ft/sec2 Now let’s suppose that the moon’s orbit was caused to increase so that it became situated 400,000 miles, or 2,112,000,000 feet from Earth. Earth’s acceleration of gravity exerted upon the moon at this distance would be calculated as: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (2,112,000,000 ft)2 g = 0.0032 ft/sec2 From these two examples we can see that the further the moon is positioned from Earth, the weaker Earth’s gravitational pull upon it is. This gravitational pull is the force of gravity, Fg, introduced in our last blog, a term which originates in Newton’s Second Law of Motion, as given by the equation: Fg = m × g (2) where, in this case, m represents the mass of the moon. Next time we’ll combine equations (1) and (2) and derive a third formula which will allow us to calculate the mass of the sun.
_______________________________________
|
The Force of Gravity
Thursday, November 20th, 2014|
Last time we saw how Henry Cavendish built upon the work of scientists before him to calculate Earth’s mass and its acceleration of gravity factor, as well as the universal gravitational constant. These values, together with the force of gravity value, Fg, which we’ll introduce today, moved scientists one step further towards being able to discover the mass and gravity of any heavenly body in the universe. According to Newton’s Second Law of Motion, the force of gravity, Fg, acting upon any object is equal to the object’s mass, m, times the acceleration of gravity factor, g, or, Fg = m × g So what is Fg? It’s a force at play way up there, in the outer reaches of the galaxy, as well as back home. It keeps the moon in orbit around the Earth and the Earth orbiting around the sun. In the same way, Fg keeps us anchored to Earth, and if we were to calculate it, it would be calculated as the force of our body’s mass under the influence of Earth’s gravity. It’s common to refer to this force as weight, but it’s not quite so simple. Using the metric system, the unit of measurement most often used for scientific analyses, weight is determined by multiplying our body’s mass in kilograms by the Earth’s acceleration of gravity factor of 9.8 meters per second per second, or 9.8 meters per second squared. For example, suppose your mass is 100 kilograms. Your weight on Earth would be: Weight = Fg = m × g = (100 kg) × (9.8 m/sec2) = 980 kg · m/sec2 = 980 Newtons Newtons? That’s right. It’s easier than saying kilogram · meter per second per second. It’s also a way to pay homage to the man himself. In the English system of measurement things are perhaps even more confusing. Your weight is found by multiplying the mass of your body measured in slugs by the Earth’s acceleration of gravity factor of 32 feet per second per second. Slugs is British English speak for pounds · second squared per foot. We normally refer to weight in units of pounds, and in engineering circles it’s pounds force. For example, suppose your mass is 6 slugs, or 6 pounds · second squared per foot. Your weight on Earth would be: Weight = Fg = m × g = (6 Lbs · sec2/ft) × (32.2 ft/sec2)= 193.2 Lbs To avoid any confusion, you could just step on the bathroom scale. Next time we’ll see how the force of gravity is influenced by an inverse proportionality phenomenon. _______________________________________
|