|
Last time we learned how Henry Cavendish used Christiaan Huygens’ work with pendulums to determine the value of g, the acceleration of gravity factor for Earth, to be 32.3 ft/sec2, or 9.8 m/sec2. From there Cavendish was able to go on and arrive at values for other factors in Isaac Newton’s gravity formula, namely G, the universal gravitational constant, and M, Earth’s mass. Today, we’ll discuss how Cavendish was able to calculate the Earth’s mass. Newton’s formula for gravity, once again, is: M = (g × R2) ÷ G where M stands for the mass of the heavenly body being quantified. For our case today M will represent the mass of Earth, which was originally quantified in slugs, a British unit of measurement. Today the measurement unit of choice in most parts of the world is the kilogram, which is the metric equivalent of a slug. With regard to the other variables in Newton’s gravity formula, namely, R and G, their values had previously been determined. Eratosthenes’ measurement of shadows cast by the sun on Earth’s surface had revealed Earth’s radius, R, to be 6,371 kilometers, or 6,371,000 meters. And Cavendish’s experiments led him to conclude that the universal gravitational constant, G, was 6.67 × 10-11 cubic meters per kilogram-second squared. Plugging these values into Newton’s equation, we calculate Earth’s mass to be: M = ((9.8 m/sec2) × (6,371,000 m)2) ÷ (6.67 × 10-11 m3/kg-sec2) M = 5.96 × 1024 kilograms Incidentally, 5.96 × 1024 is scientific notation, or mathematical shorthand, for the number 5,960,000,000,000,000,000,000,000. That’s a whole lot of zeros! Calculating the mass of Earth was an impressive accomplishment. Now that its value was known, scientists would be able to calculate the mass and acceleration of gravity for any heavenly body in the universe. We’ll see how that’s done next time.
_______________________________________
|
Posts Tagged ‘forensic engineer’
What is Earth’s Mass?
Friday, November 7th, 2014
How Long is a Pendulum’s Swing?
Wednesday, October 29th, 2014|
What would you do to pass the time if you were stuck on a ship of the middle ages for weeks at a time? Dutch mathematician Christiaan Huygens used the time to study the movement of clock pendulums. He watched them for endless hours, and he eventually came to realize that the pendulums’ swing was uneven due to the ship’s listing on the waves, a phenomenon which also affected the ship’s clocks’ accuracy. Eager to devise a solution to the problem of inaccurate time keeping, Huygens dedicated himself to finding a solution to the problem, and in so doing increase the navigational accuracy of ships as well. His efforts eventually resulted in a formula that shared a common variable with Isaac Newton’s gravitational formula, namely, g, Earth’s acceleration of gravity factor, a value which Huygens posited was indeed a non varying constant.
Building upon Newton’s work, Huygens devised a formula which demonstrated the mathematical relationship between the motion of a clock’s pendulum and g. That formula is, T = 2 × ∏ × (L ÷ g)1/2 where, T is the period of time it takes a pendulum to make one complete swing, ∏ the Greek symbol pi, valued at 3.14, and L the length of the pendulum. Since devices capable of directly measuring the Earth’s gravity did not exist then, as they still don’t exist today, how in the world (pardon the pun) was Huygens able to arrive at this formula? Thinking outside the box, he posited that if one knows the length of the pendulum L, and then accurately measures the time it takes for the pendulum to complete its swings, taking into account the varied times that resulted due to the ship’s listing, one can calculate g using his equation. He eventually determined g‘s value to be equal to 32.2 feet per second per second, or 32.2 ft/sec2. Fast forwarding to Henry Cavendish’s time, Huygens’ work with pendulums and his determination of g was well known. We’ll see what Cavendish did with this knowledge next time.
_______________________________________
|
Huygens’ Use of Pendulums
Tuesday, October 21st, 2014|
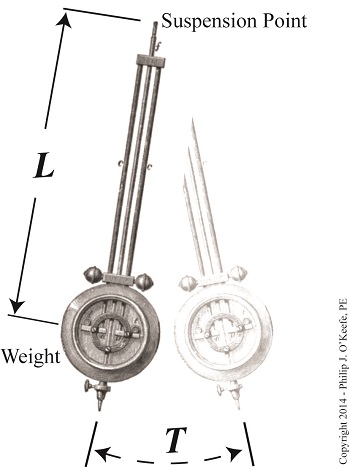
Last time we learned that Henry Cavendish determined a value for G, the universal gravitational constant, fast on his way to determining a quantity he was determined to find, the Earth’s mass. Today we’ll see how the previous work of Christiaan Huygens, a contemporary of Isaac Newton’s, helped him get there. First Cavendish used algebra to rearrange terms in Newton’s gravitational formula so as to solve for M, Earth’s mass. Rearranged, Newton’s formula becomes, M = (g × R2) ÷ G But in order to solve for M, Cavendish first needed to know Earth’s acceleration of gravity, g. To aid him in this calculation he referred back to the work of Christiaan Huygens, a Dutch mathematician from Newton’s time.
Huygens was eager to devise a formula capable of predicting clock pendulums’ motions on ships, his goal being to invent a timepiece accurate enough to make navigating ships easier. He hypothesized that a key factor in predicting a pendulum’s movement was an unknown constant, the acceleration of gravity factor, g, which Newton had previously posited existed. Through meticulous observation, Huygens came to realize that the time it took for pendulums to complete one swing back and forth was dependent not only on the length of the pendulum, but also this unknown quantity. In order for Huygens’ computations to work, the value of g had to be a constant, meaning, its value could not vary between computations; g‘s value was in fact a fudge factor, a phantom he would assign a specific numerical value. Huygens’ needed it in order to make his hypothesis work, a practice commonly use by scientists, even today. Determining a value for g would allow Huygens to successfully relate the length of the pendulum to the timing of its swing and to create a mathematical relationship between them. Huygens ultimately determined g’s value to be a whopping 32.2 feet per second per second, or 32.2 ft/sec2. We’ll see how he did it next time.
_______________________________________
|
How Big is the Earth?
Wednesday, October 8th, 2014|
Last time we discussed Isaac Newton’s Law of Gravitation and how he used it to arrive at conclusions concerning gravity. He theorized the existence of a universal gravitational constant, G, a set numerical value for all heavenly bodies in our universe, and he developed a formula to determine the acceleration of gravity, g. Newton felt sure that the gravity at play on the surface of any heavenly body, such as stars and planets, could be determined if one knew the value of G, along with the object’s mass, M, and radius, R, and he developed this equation to do so, g = (G × M) ÷ R2 At this point you may be thinking, Finding the mass and radius of a heavenly body is hard enough, but what is this universal gravitational constant?? Good point. Back in Newton’s time, the existence of G was purely speculative. He conceived it to be a numerical value which would act as a fudge factor, enabling his equation for determining g to work. As a matter of fact, Newton had no clue of how to determine G and was convinced that it would be beyond anyone’s ability to do so. The mysterious G factor and its numerical value were not actually determined until more than a hundred years later by Henry Cavendish. In 1796 Cavendish was focused on determining the Earth’s mass, M, by using Newton’s equation. To arrive at a value for G, Cavendish conducted experiments which measured the gravitational attraction between two lead spheres attached by way of a torsion balance. After much testing he eventually concluded that he had computed G to a reasonable degree of accuracy and that its value was equal to 3.439 x 10-8 cubic feet per slug per second squared. In this case a slug is not a slimy creature living in the garden, but rather a unit of measurement used to quantify the mass of an object. For the full story, see this article on Cavendish’s experiment by The Physics Classroom. But even after determining G, Cavendish still had to obtain values for g and R in order to calculate M. This was made possible thanks to the work of two men who came before him. One of these was the Greek mathematician Eratosthenes, who way back in 230 B.C. discovered that the radius of the earth, R, could be calculated by simply measuring the shadows of objects cast on Earth’s surface. All he needed was a measuring stick and geometry. For the full story see this fascinating article on the subject from Bucknell University.
As for the value of g, the acceleration of gravity on Earth, Cavendish was aided by the previous efforts of a Dutch mathematician from Newton’s time, Christiaan Huygens. You may recall that Huygens was first introduced in a previous blog series on spur gear geometry, where we learned that he studied the motion of clock pendulums. Through observation, Huygens was able to arrive at a mathematical formula capable of predicting the pendulums’ often erratic motion on ships at sea. Next time we’ll see how Huygens’ insights gained by watching pendulums ultimately made it possible for him to arrive at a numerical value for Earth’s acceleration of gravity, g. _______________________________________
|
Newton’s Law of Gravitation and the Universal Gravitational Constant
Monday, September 29th, 2014|
Last time we introduced the term acceleration of gravity, a physical phenomenon posited by Sir Isaac Newton in his book Philosophia Naturalis Principia Mathematica. Newton’s Law of Gravitation is also presented in this book. It provides the basis for his mathematical formula to calculate the acceleration of gravity, g, for any heavenly body in the universe. Newton’s formula to compute the acceleration of gravity is, g = (G × M) ÷ R2 where, g is the acceleration of gravity, M the mass of the heavenly body, R the radius, and G the universal gravitational constant. As for the values of the variables in his equation, Newton theorized that G would be a constant, holding the same numerical value throughout the universe. This universal gravitational constant would be the glue that bound together M, the mass of the object being measured, and R, its radius, and render Newton’s formula a workable equation. Without these three values, scientists would be unable to determine the acceleration of gravity rate, g, for the heavenly body under study, and Newton’s equation would be useless, relegated to the depths of pure mathematical theory. In fact, the value for G wasn’t determined until 1796. At that time Henry Cavendish derived its value as an adjunct to calculating the mass of Earth. In the end he was able to arrive at values for Earth’s mass, M, as well as its radius, R. He also came up with the much needed value for G, the universal gravitational constant. He was able to accomplish so much by building upon the work of other scientists before him. We’ll see who those earlier scientists were and how they contributed to the world’s discoveries concerning gravity next time.
_______________________________________
|
Sir Isaac Newton and the Acceleration of Gravity
Thursday, September 18th, 2014|
Last time we watched a video of Astronauts Scott and Irwin simultaneously dropping a hammer and feather to the surface of the Moon and were amazed to find that the objects struck the surface at exactly the same time. It was history in the making, and Galileo’s theory regarding gravity was proven beyond a shadow of a doubt. If you watched the video of the event very closely, it might have struck you that the hammer was falling more slowly than it would had it been dropped on Earth, and you’d be right. Let’s find out why. Sir Isaac Newton was a pioneer in this subject matter. According to his book, Philosophia Naturalis Principia Mathematica, first published in 1687, every heavenly body in the universe, whether it be planet, moon, or star, generates gravity, and any object in freefall towards its surface will be subject to that gravity. He posited that the falling object will gain speed at a constant rate as it falls, that constant speed being dictated by the acceleration of gravity factor that’s at play on the heavenly body it’s falling toward.
For example, if the acceleration due to gravity on a small planet is, say, 2 feet per second per second, after one second of falling, an object’s velocity will be 2 feet per second. After two seconds of falling, the object will have accelerated to a velocity of 4 feet per second. After three seconds, the object’s velocity will have accelerated to 6 feet per second, and so on. In other words, the speed, or velocity, of the object’s descent will increase for every second it falls closer to the surface of the planet, a phenomenon which is measured in units of feet per second (ft/sec). The acceleration of gravity of a falling object is the linear increase in its velocity that takes place during each succeeding second of its fall, a phenomenon which is measured in feet per second per second (ft/sec2). Next time we’ll discuss the formula which enables us to calculate gravitational acceleration. We have Sir Isaac to thank for that one, too. _______________________________________
|
Proving Galileo’s Theory On Falling Objects
Thursday, September 11th, 2014|
Last time we discussed how Galileo proved Aristotle’s theory regarding the physics of falling objects to be wrong, although his experiment, which took place on the infamous Leaning Tower of Pisa, did not actually prove his own theory to be correct. So why didn’t Galileo go the extra mile and prove his theory? Because he couldn’t. Galileo, of course, resided on Earth, which was also the arena in which his experiment took place. As such, both he and his experiment were subject to the physical constraints presented by the Earth lab, the single most influential factor being the impact of the planet’s atmosphere upon his falling objects. Put another way, contrary to popular belief at the time, air is not an empty, innocuous space devoid of physical properties. It’s actually a gaseous soup of molecules. Nitrogen, oxygen, carbon, hydrogen, and other elements are in the mix, and they all have mass, that is, weight within a gravitational field. As Galileo’s balls fell, they continuously bumped against these molecules, which slowed their descent. This air friction will be discussed later in our blog series. But in order to prove Galileo’s theory correct beyond a shadow of a doubt, the testing arena would need to be one free from the interference of atmosphere. The Moon fits this criterion and provided the perfect environment to prove, once and for all, that Galileo’s theory was correct. So when astronauts Scott and Irwin simultaneously dropped a hammer and feather to the Moon’s surface, both objects hit at precisely the same moment. Watch this captured live footage of the event to see for yourself: One thing you may have noticed while watching the astronauts’ experiment is that the hammer fell more slowly than it would have on Earth. This has nothing to do with the absence of atmosphere on the Moon, but it has everything to do with gravity. We’ll discuss gravity’s influence in detail next time. _______________________________________
|
What Determines Rate of Fall?
Thursday, September 4th, 2014|
Picture yourself holding a feather in one hand, a hammer in the other. Your buddy has bet you that if you simultaneously drop them, the hammer will hit the ground first, and he’s got a beer riding on it. This exact experiment was performed in 1971 by Apollo 15 Astronauts David Scott and Jim Irwin when they landed on the moon. We’ll tell you how it turned out later, but first let’s review the history behind the study of falling objects. Aristotle, the ancient Greek philosopher, would have bet with your buddy. Back in the 4th Century BC he developed a theory of gravity to explain the physics behind falling objects. He asserted that the heavier the object, the faster it will fall. His theory seems intuitively obvious on its face, but although Aristotle was a great philosopher, he was a lousy scientist. He never ran tests to actually prove his theory. Nevertheless, it was accepted by academics of his time, and it remained the theory of choice until Galileo came along in the 16th Century. Galileo was a scientist, and he came up with his own theory concerning falling objects. He believed that all falling objects continue to accelerate, picking up speed as they fall, and that this rate of acceleration is the same for all objects, regardless of their weight or density. The story goes that in 1589, at the age of 25, young Galileo attempted to prove his theory by climbing to the top of the Leaning Tower of Pisa with two balls in hand, one large and heavy, the other small and light. He dropped them at the same time, and guess what happened?
Both balls hit the ground at almost the same time. They would have hit the ground at precisely the same moment had there been no air resistance, a subject which will be discussed at length later in this blog series. Because Galileo’s experiment was subject to the dense atmosphere of Earth, the influence of air resistance prevented him from proving his theory correct, however he did manage to prove Aristotle’s theory wrong because the balls did not strike the ground at significantly different times. We’ll see how the astronauts’ experiment turned out next time.
_______________________________________
|
Determining the Gear Train Tradeoff of Torque vs. Speed, Part Three
Wednesday, August 27th, 2014|
We’ve been working towards a general understanding of how gear trains work, and today we’ll solve a final piece of the puzzle when we identify how increased gear train torque is gained at the expense of gear train speed. Last time we developed a mathematical relationship between the torque, T, and the rotational speed, n, of the driving and driven gears in a simple gear train. This is represented by equation (8): TDriven ÷ TDriving = nDriving ÷ nDriven (8) For the purpose of our example we’ll assume that the driving gear is mounted to an electric motor shaft spinning at 100 revolutions per minute (RPM) and which produces 50 inch pounds of torque. Previous lab testing has determined that we require a torque of 100 inch pounds to properly run a piece of machinery that’s powered by the motor, and we’ve decided that the best way to get the required torque is not to employ a bigger, more powerful motor, but rather to install a gear train and manipulate its gear sizes until the desired torque is obtained. We know that using this approach will most likely affect the speed of our operation, and we want to determine how much speed will be compromised. So if the torque on the driven gear needs to be 100 inch pounds, then what will be the corresponding speed of the driven gear? To answer this question we’ll insert the numerical information we’ve been provided into equation (8). Doing so we arrive at the following: TDriven ÷ TDriving = nDriving ÷ nDriven (100 inch pounds) ÷ (50 inch pounds) = (100 RPM) ÷ nDriven 2 = (100 RPM) ÷ nDriven nDriven = (100 RPM) ÷ 2 = 50 RPM This tells us that in order to meet our torque requirement of 100 inch pounds, the gear train motor’s speed must be reduced from 100 RPM to 50 RPM, which represents a 50% reduction in speed, hence the tradeoff.
This wraps up our blog series on gears and gear trains. Next time we’ll move on to a new topic: Galileo’s experiments with falling objects.
_______________________________________
|
Determining the Gear Train Tradeoff of Torque vs. Speed, Part Two
Wednesday, August 20th, 2014|
In this blog series we’ve been examining gear train usefulness, specifically in terms of increasing torque. Equations presented last week began us on the final leg of our journey, and we’ve arrived at the point where the closing combination of equations will demonstrate the loss of speed that takes place when torque is increased within a gear train. To that end, the two main equations under consideration as presented last week, are:
where R is the gear ratio of the gear train, N is the number of gear teeth, n is the gear rotational speed in revolutions per minute (RPM), T is the torque, and D is the gear pitch radius. We were able to link these two equations by working through five key design equations applicable to simplified gear trains. For the full step-by-step progression see last week’s blog.  After working through the equations presented last time we were able to arrive at an equation which links equations (1) and (2). Here it is:
If you follow the color coding, you’ll see the elements of equations (1) and (2) which come together in equation (7). Because equation (7) links the gear speed ratios (red) with the gear pitch radii ratios (green), we can set the ratios in equation (1) equal to those in equation (2). Doing so, we get: R = NDriven ÷ NDriving = nDriving ÷ nDriven = DDriven ÷ DDrivng = TDriven ÷ TDriving
In order to see the tradeoff between speed and torque, we need only consider the parts of the equation which concern themselves with factors relating to speed and torque. Removing the other unnecessary factors, we arrive at:
Next week we’ll plug numbers into equation (8) and disclose the tradeoff of speed for torque.
_______________________________________
|
