|
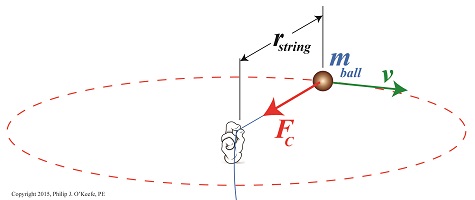
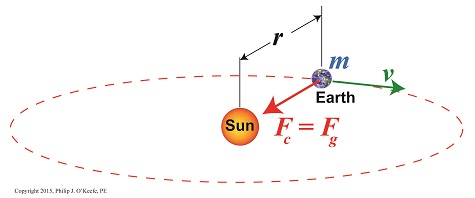
Last time we saw how centripetal force is responsible for keeping a child’s ball moving in a circular path when twirled above his head. Today we’ll see how that same force is responsible for keeping Earth in its rotation around the sun. We’ll use Isaac Newton’s Second Law of Motion as it relates to centripetal force to bear that out today. Our example from last week, Figure 1 According to Newton’s Second Law of Motion, Fc, the centripetal force acting upon the ball, is calculated by the equation, Fc = [mball × v2] ÷ rstring where, mball is the ball’s mass, v the ball’s velocity, and rstring is the length of the string. The mechanics are obviously different with regard to Earth and its orbit around the sun, where there’s no obvious physical link between the objects in rotation. In this case the sun’s gravitational force, Fg, acts to tether Earth to it. And just like the string and ball, the sun’s gravitational tether creates a centripetal force, Fc, which prevents Earth from leaving its orbital path. See Figure 2. Figure 2 Newton concluded that for the Earth to remain on its permanent, fixed path of orbit around the sun, Fc must be equal to Fg, and that the forces in play between the sun and Earth were like a gigantic tug of war where neither side is able to pull any harder than the other. This stalemate is responsible for keeping Earth stably in place in its orbit. According to Newton’s Second Law, the sun’s gravitational force acting upon the Earth is calculated by, Fg = Fc = [m × v2] ÷ r where, m is Earth’s mass, v its orbital velocity, and r the distance between Earth and the sun. Thanks to early scientists like Edmund Halley and Henry Cavendish, the values for m and r had already been determined. That left v, Earth’s orbital velocity, the only variable remaining to be solved. We’ll see how 19th Century scientists accomplished that next time.
____________________________________
|
Posts Tagged ‘gravitational force’
Centripetal Force Makes the Earth Go Round
Thursday, July 9th, 2015The Inverse Relationship of the Acceleration of Gravity
Friday, December 5th, 2014|
In this blog series we’ve been working our way towards determining mass values for heavenly bodies in our universe. Today we’ll explore the inverse relationship phenomenon that’s present when examining the acceleration of gravity between two heavenly bodies, for our purposes Earth and its moon. To demonstrate the inverse relationship phenomenon, we’ll use Newton’s Law of Gravitation formula: g = (G × M) ÷ r2 (1) In this formula g represents Earth’s acceleration of gravity that’s acting upon the moon. The center of the moon is located at a distance r from Earth’s center. Earth’s mass is represented by M, and G is the universal gravitational constant, which never varies from its value of 3.49 × 10-8 cubic feet per slug per second squared. We’ll solve for Earth’s g factor relative to the moon, which we’ll position at varying distances from Earth’s core, thereby demonstrating how the attracting force of Earth’s gravity becomes weaker as the moon’s distance from Earth’s core increases — hence the inverse relationship. To begin, we know that the present distance from Earth’s center to the center of the moon is about 238,900 miles, or 1,261,392,000 feet. We also know that Earth’s mass, M, is equal to 4.09 × 1023 slugs. Plugging these values into Newton’s Law of Gravitation equation, we calculate the acceleration of gravity exerted upon the moon in this, its normal orbit, to be: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (1,261,392,000 ft)2 g = 0.0089 ft/sec2 Now let’s suppose that the moon’s orbit was caused to increase so that it became situated 400,000 miles, or 2,112,000,000 feet from Earth. Earth’s acceleration of gravity exerted upon the moon at this distance would be calculated as: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (2,112,000,000 ft)2 g = 0.0032 ft/sec2 From these two examples we can see that the further the moon is positioned from Earth, the weaker Earth’s gravitational pull upon it is. This gravitational pull is the force of gravity, Fg, introduced in our last blog, a term which originates in Newton’s Second Law of Motion, as given by the equation: Fg = m × g (2) where, in this case, m represents the mass of the moon. Next time we’ll combine equations (1) and (2) and derive a third formula which will allow us to calculate the mass of the sun.
_______________________________________
|