|
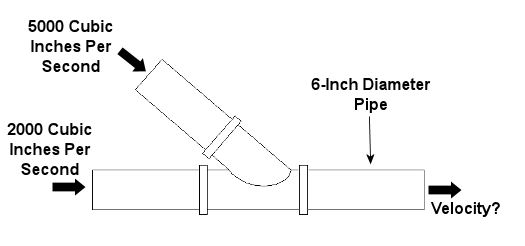
Last week, we learned about some general properties of fluids, concentrating on fluid statics, which is concerned with fluids that don’t move. This week we’ll consider a more dynamic situation, one in which the fluids do move. Remember how we talked about incompressible fluids in the first part of this series on fluid mechanics? We learned that an incompressible fluid, like the oil in a hydraulic jack, can’t be squeezed down into a smaller volume under pressure, so its volume will always remain the same. The same thing goes for other incompressible fluids, like water. By the same token, when water flows through a length of pipe, its volumetric flow rate will remain the same from beginning to end.. By “volumetric flow rate,” I mean the volume of water flowing through the pipe in a given amount of time. It’s measured in cubic inches per second (in3/sec). Now let’s revisit our discussion on the stoichiometry segment of our series on thermodynamics. It’s there that we learned that mass cannot be created or destroyed, and this concept is known as the “conservation of mass.” Applying this principle to incompressible fluids with mass, like water, we can essentially expand on that to say that volume, like mass, can’t be created or destroyed. Because of this, the volumetric flow rate entering the pipe has to equal the flow rate exiting, regardless of whether the pipe diameter changes and whether there are multiple inlets and outlets on the pipe. This volumetric flow rate is related to the velocity, or speed, of water flowing through a round pipe, as well as the interior diameter of the pipe, and it is calculated by this equation: Volumetric Flow Rate = V = (v) x (πd2/4) where “V” is the velocity of the water flowing through the pipe and “d” is the inside diameter of the pipe. The “πd2/4” part of the equation is the cross sectional area of the round pipe. This is derived from the formula used to measure the area of a circle, where the circle’s diameter is “d.” The volumetric flow rate equation above is very useful for designing piping systems used to move of fluids like water from one place to the other. For example, the equation can be used to design the piping system of a municipal water treatment plant. Waste water in, clean water out. Now let’s look at an example. Let’s consider water flowing into the pipe shown in Figure 1 below. If we know the volumetric flow rates of the water going into the two branches, then what would be the velocity of the water coming out?
Figure 1 – A Pipe With Water Flowing Through It
For this problem, let’s use the concept of conservation of volume discussed above and combine it with our volumetric flow rate equation. Applying algebra, we can use the information we are given in Figure 1 to find the solution: Volumetric Flow Rate Going In = Volumetric Flow Rate Going Out VGoing In = VGoing Out VGoing In = [(v) x (πd2/4)]Going Out (VGoing In) / (πd2/4) = vGoing Out vGoing Out = (5000 in3/sec + 2000 in3/sec) / ((π) x (6 in)2/4) = 247.6 in/sec So the water would come shooting out of the pipe at a speed of 247.6 inches per second. That’s pretty fast! Next week we’ll continue with our series on fluid mechanics and explore the Bernoulli principle. By doing so, we’ll examine what’s behind the function of airplane wings and how they enable planes to fly. _________________________________________________________________ |
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE