|
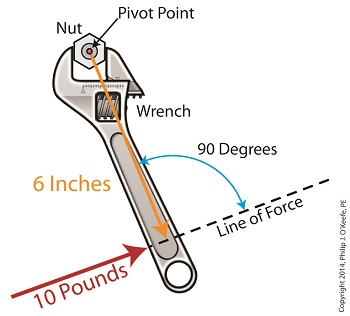
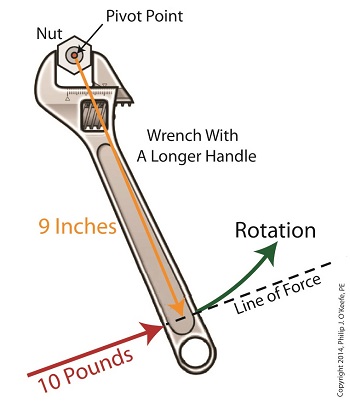
Last time we introduced the simplified formula for torque: Torque = Distance × Force Today we’ll manipulate it by way of our wrench and nut example to get the torque that we need to loosen a tight nut. By inserting the numerical values of our illustration into the torque formula, it becomes: Torque = 6 inches × 10 pounds = 60 inch-pounds Inch-pounds may be terminology you’re unfamiliar with, but this notation arises from the fact that torque values are always represented by units of distance and force separated by a hyphen, in our case inch-pounds. This just means that distance and force were multiplied together to calculate torque. In order to manipulate the value for torque all that needs to be done is change either or both numerical values for Distance and Force. Increasing either or both factors produces higher torque, decreasing them less torque. Why manipulate torque? To provide us with a mechanical advantage. Suppose we have a rusted nut that we’re trying to move with a wrench that has a 6 inch handle, and the 10 pounds of force employed by the muscles in our arm just won’t budge it. Put another way, 60 inch-pounds of torque is insufficient to rotate the nut. It’s clear we must increase torque to get things going. Let’s do so by increasing either of the vector magnitudes. First we’ll try increasing the magnitude of the force vector. Instead of simply pushing hard on the wrench handle with our arm, let’s say we push extra hard. The average man can do a bicep curl of between 30 to 40 pounds, but we haven’t been going to the gym lately and we’re really out of shape. So try as we will, we just can’t muster up the bicep strength to apply more than 10 pounds of force to the wrench handle. It’s clear that this approach to increasing torque upon the nut isn’t going to work. The other way to increase torque is to increase the length of the distance vector. We’ll need a wrench with a longer handle, say 9 inches. By using a wrench with a longer handle we have increased the magnitude of the distance vector from 6 to 9 inches. The torque formula becomes: Torque = 9 inches × 10 pounds = 90 inch-pounds Eureka! The longer handle has provided us with the mechanical advantage needed to increase torque to 90 inch-pounds, thereby overcoming our muscular shortcomings and breaking the nut free. In summary, since torque is the product of the magnitudes of the distance and force vectors, we can increase torque by either increasing the magnitude of the force vector, or as in our example, by increasing the magnitude of the distance vector. Next time we’ll see how to apply the principles of torque to a real world situation involving gear trains in which we need to obtain a mechanical advantage. _______________________________________ |
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE