|
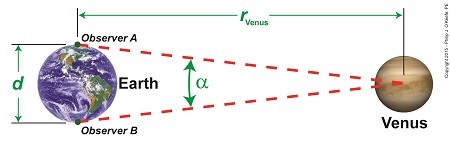
We’ve been paying a lot of attention to Venus and its orbital patterns, as did scientist Edmund Halley hundreds of years ago. Back then he came up with a plan to determine Earth’s distance to the sun, the AU. Two key components were Kepler’s Astronomical Unit, or AU, and an angle, α, which formed between lines of sight followed by observers on Earth during the Transit of Venus. Halley theorized that α together with Kepler’s Third Law of Planetary Motion would make it possible to calculate the AU. We’ll see how today. Figure 1 Figure 1 depicts what Halley had in mind. He theorized that if observers positioned on opposite sides of Earth could determine the precise times it took Venus to travel across the sun’s face from each of their perspectives, they could use this information together with previously gathered information on the time it takes Earth and Venus to make a complete orbit around the sun. This would allow the angle α to be calculated, and from that Earth’s distance to Venus, rVenus. Halley’s calculations for α are beyond the scope of this series, but if you’re interested in reading more about them, you can follow this link. Earth’s distance to Venus, rVenus, is computed in a manner similar to the method we used previously to determine Earth’s distance to the moon, by using this equation, r = d × tan(θ) For a refresher on the subject, follow this link to my past blog on Optically Measuring Cosmic Distances. And here’s the same equation modified to solve for the distance between Earth and Venus, rVenus, rVenus = d ÷ tan(α) (1) Once Earth’s distance to Venus was determined, its value was incorporated into Kepler’s equation for 1 AU, and the distance between Earth and the sun became known. Here again is the equation from Kepler’s Third Law of Planetary Motion, 1 AU = rVenus ÷ 0.28 (2) And here it is with the function for rVenus from equation (1) inserted into equation (2) to solve for 1 AU, 1 AU = [d ÷ tan(α)] ÷ 0.28 1 AU = d ÷ [0.28 × tan(α)] (3) From equation (3) the distance between Earth and the sun, 1 Astronomical Unit, was calculated to be between 92,000,000 and 96,000,000 miles. Unfortunately, a Transit of Venus did not occur within Halley’s lifetime, but scientists that followed him applied his methodology after the next Transit occurred in 1761. Since that time modern technology and the radar have improved measuring accuracy so that we now know the sun is located 92,935,700 miles from Earth. Next time we’ll return full circle to our opening topic in this long blog series when we reopen our discussion on gravity, specifically, how the concept of centripetal force is instrumental in determining the gravitational force exerted upon Earth by the sun.
____________________________________
|
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE