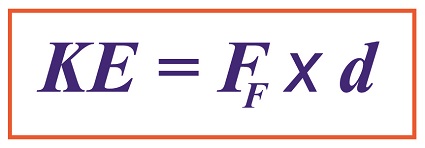Posts Tagged ‘kinetic energy’
Wednesday, May 25th, 2016
|
My activities as an engineering expert often involve creative problem solving of the sort we did in last week’s blog when we explored the interplay between work and kinetic energy. We used the Work-Energy Theorem to mathematically relate the kinetic energy in a piece of ceramic to the work performed by the friction that’s produced when it skids across a concrete floor. A new formula was derived which enables us to calculate the kinetic energy contained within the piece at the start of its slide by means of the work of friction. We’ll crunch numbers today to determine that quantity.
The formula we derived last time and that we’ll be working with today is,
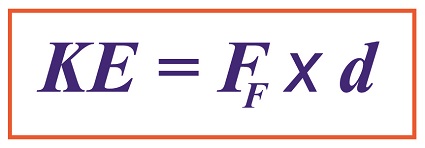 Calculating Kinetic Energy By Means of the Work of Friction
where, KE is the ceramic piece’s kinetic energy, FF is the frictional force opposing its movement across the floor, and d is the distance it travels before friction between it and the less than glass-smooth floor brings it to a stop.
The numbers we’ll need to work the equation have been derived in previous blogs. We calculated the frictional force, FF, acting against a ceramic piece weighing 0.09 kilograms to be 0.35 kilogram-meters/second2 and the measured distance, d, it travels across the floor to be equal to 2 meters. Plugging in these values, we derive the following working equation,
KE = 0.35 kilogram-meters/second2 × 2 meters
KE = 0.70 kilogram-meters2/second2
The kinetic energy contained within that broken bit of ceramic is just about what it takes to light a 1 watt flashlight bulb for almost one second!
Now that we’ve determined this quantity, other energy quantities can also be calculated, like the velocity of the ceramic piece when it began its slide. We’ll do that next time.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, electrical energy, energy, engineering expert, frictional force, kinetic energy, mass, velocity, Watt, work, work of friction, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Calculating Kinetic Energy By Means of the Work of Friction
Thursday, May 12th, 2016
|
We’ve been discussing the different forms energy takes, delving deeply into de Coriolis’ claim that energy doesn’t ever die or disappear, it simply changes forms depending on the tasks it’s performing. Today we’ll combine mathematical formulas to derive an equation specific to our needs, an activity my work as an engineering expert frequently requires of me. Our task today is to find a means to calculate the amount of kinetic energy contained within a piece of ceramic skidding across a concrete floor. To do so we’ll combine the frictional force and Work-Energy Theorem formulas to observe the interplay between work and kinetic energy.
As we learned studying the math behind the Work-Energy Theorem, it takes work to slow a moving object. Work is present in our example due to the friction that’s created when the broken piece moves across the floor. The formula to calculate the amount of work being performed in this situation is written as,
W = FF ×d (1)
where, d is the distance the piece travels before it stops, and FF is the frictional force that stops it.
We established last time that our ceramic piece has a mass of 0.09 kilograms and the friction created between it and the floor was calculated to be 0.35 kilogram-meters/second2. We’ll use this information to calculate the amount of kinetic energy it contains. Here again is the kinetic energy formula, as presented previously,
KE = ½ × m × v2 (2)
where m represents the broken piece’s mass and v its velocity when it first begins to move across the floor.
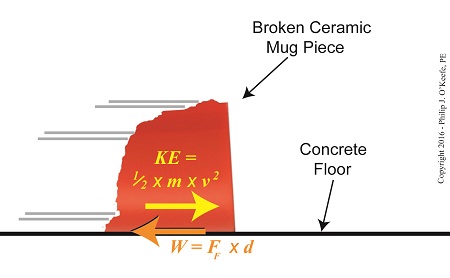
The Interplay of Work and Kinetic Energy
The Work-Energy Theorem states that the work, W, required to stop the piece’s travel is equal to its kinetic energy, KE, while in motion. This relationship is expressed as,
KE = W (3)
Substituting terms from equation (1) into equation (3), we derive a formula that allows us to calculate the kinetic energy of our broken piece if we know the frictional force, FF, acting upon it which causes it to stop within a distance, d,
KE = FF × d
Next time we’ll use this newly derived formula, and the value we found for FF in our previous article, to crunch numbers and calculate the exact amount of kinetic energy contained with our ceramic piece.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, energy, engineering expert, frictional force, kinetic energy, mass, velocity, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Interplay of Work and Kinetic Energy
Wednesday, April 27th, 2016
|
Last time we introduced the frictional force formula which is used to calculate the force of friction present when two surfaces move against one another, a situation which I as an engineering expert must sometimes negotiate. Today we’ll plug numbers into that formula to calculate the frictional force present in our example scenario involving broken ceramic bits sliding across a concrete floor.
Here again is the formula to calculate the force of friction,
FF = μ × m × g
where the frictional force is denoted as FF, the mass of a piece of ceramic sliding across the floor is m, and g is the gravitational acceleration constant, which is present due to Earth’s gravity. The Greek letter μ, pronounced “mew,” represents the coefficient of friction, a numerical value predetermined by laboratory testing which represents the amount of friction at play between two surfaces making contact, in our case ceramic and concrete.
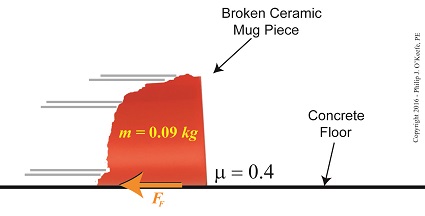
To calculate the friction present between these two materials, let’s suppose the mass m of a given ceramic piece is 0.09 kilograms, μ is 0.4, and the gravitational acceleration constant, g, is as always equal to 9.8 meters per second squared.
Calculating the Force of Friction
Using these numerical values we calculate the force of friction to be,
FF = μ × m × g
FF = (0.4) × (0.09 kilograms) × (9.8 meters/sec2)
FF = 0.35 kilogram meters/sec2
FF = 0.35 Newtons
The Newton is shortcut notation for kilogram meters per second squared, a metric unit of force. A frictional force of 0.35 Newtons amounts to 0.08 pounds of force, which is approximately equivalent to the combined stationary weight force of eight US quarters resting on a scale.
Next time we’ll combine the frictional force formula with the Work-Energy Theorem formula to calculate how much kinetic energy is contained within a single piece of ceramic skidding across a concrete floor before it’s brought to a stop by friction.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: coefficient of friction, Earth's gravity, engineering expert, force of friction, friction, frictional force, frictional force formula, gravitational acceleration constant, kinetic energy, Newtons, weight force, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Calculating the Force of Friction
Monday, April 4th, 2016
|
Humans have been battling the force of friction since the first cave man built the wheel. Chances are his primitive tools produced a pretty crude wheel that first go-around and the wheel’s surfaces were anything but smooth, making its usefulness less than optimal. As an engineering expert, I encounter these same dynamics when designing modern devices. What held true for the cave man holds true for modern man, friction is often a counterproductive force which design engineers must work to minimize. Today we’ll learn about frictional force and see how it impacts our example broken coffee mug’s scattering pieces, and we’ll introduce the man behind friction’s discovery, Charles-Augustin de Coulomb.

Charles-Augustin de Coulomb
Last time we learned that the work required to shatter our mug was transformed into the kinetic energy which propelled its broken pieces across a rough concrete floor. The broken pieces’ energetic transformation will continue as the propelling force of kinetic energy held within them is transmuted back into the work that will bring each one to an eventual stop a distance from the point of impact. This last source of work is due to the force of friction.
In 1785 Charles-Augustin de Coulomb, a French physicist, discovered that friction results when two surfaces make contact with one another, and that friction is of two types, static or dynamic. Although Leonardo Da Vinci had studied friction hundreds of years before him, it is Coulomb who is attributed with doing the ground work that later enabled scientists to derive the formula to calculate the effects of friction. Our example scenario illustrates dynamic friction, that is to say, the friction is caused by one of the surfaces being in motion, namely the mug’s ceramic pieces which skid across a stationary concrete floor.
While in motion, each of the mug’s broken pieces has its own unique velocity and mass and therefore a unique amount of kinetic energy. The weight of each piece acts as a vertical force pushing the piece down “into” the floor, this due to the influence of Earth’s gravitational pull, that is, the force of gravity.
Friction is created by a combination of factors, including the ceramic pieces’ weights and the surface roughness of both the pieces themselves and the concrete floor they skid across. At first glance the floor and ceramic mug’s surfaces may appear slippery smooth, but when viewed under magnification it’s a whole different story.
Next time we’ll examine the situation under magnification and we’ll introduce the formula used to calculate friction along with a rather odd sounding variable, mu.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: calculating frictional force, Charles-Augustin de Coulomb, contacting surfaces, dynamic friction, energetic transformation, engineering expert witness, friction, frictional force, kinetic energy, Leonardo Da Vinci, roughness, static friction, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Coulomb’s Frictional Force
Thursday, March 24th, 2016
|
Last time we watched our example ceramic coffee mug crash to a concrete floor, where its freefall kinetic energy performed the work of shattering it upon impact. This is a scenario familiar to engineering experts like myself who are sometimes asked to reconstruct accidents and their aftermaths, otherwise known as forensic engineering. Today we’ll take a look at what happens when the shattered mug’s pieces are freed from their formerly cozy, cohesive bond, and we’ll watch their transmutation from kinetic energy to work, and back to kinetic energy.
As we watch our mug shatter on the floor, we notice that it breaks into different sized pieces that are broadcast in many directions around the point of impact. Each piece has its own unique mass, m, travels at its own unique velocity, v, and has a unique and individualized amount of kinetic energy. This is in accordance with the kinetic energy formula, shown here again:
KE = ½ × m × v2
So where did that energy come from?

The Scattering Pieces Have Kinetic Energy
According to the Work-Energy Theorem, the shattered mug’s freefalling kinetic energy is transformed into the work that shatters the mug. Once shattered, that work is transformed back into kinetic energy, the energy that fuels each piece as it skids across the floor.
The pieces spray out from the point of the mug’s impact until they eventually come to rest nearby. They succeed in traveling a fair distance, but eventually their kinetic energy is dissipated due to frictional force which slows and eventually stops them.
The frictional force acting in opposition to the ceramic pieces’ travel is created when the weight of each fragment makes contact with the concrete floor’s rough surface, which creates a bumpy ride. The larger the fragment, the more heavily it bears down on the concrete and the greater the frictional force working against it. With this dynamic at play we see smaller, lighter fragments of broken ceramic cover a greater distance than their heavier counterparts.
The Work-Energy Theorem holds that the kinetic energy of each piece equals the work of the frictional force acting against it to bring it to a stop. We’ll talk more about this frictional force and its impact on the broken pieces’ distance traveled next time.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: engineering expert, force, forensic engineering, friction force, kinetic energy, kinetic energy formula, mass, velocity, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Kinetic Energy to Work, Work to Kinetic Energy
Tuesday, March 1st, 2016
|
Objects in motion inevitably meet with opposing forces, a theme which I frequently encounter in my work as an engineering expert. Today we’ll calculate the opposing force our exemplar coffee mug meets when it falls into a pan of kitty litter, thus transforming its freefalling kinetic energy into the work required to move through clay litter.
Let’s revisit the Work-Energy Theorem formula, whose terms were explained in last week’s blog,
F × d = – ½ × m × v12 (1)
The left side of this equation represents the mug’s work to move through the litter, while the right side represents its kinetic energy, which it gained through freefall. To solve for F, the amount of force acting in opposition to the mug’s mass m as it plows a depth d into the litter, we’ll isolate it on one side of the equation, as shown here,
F = [- ½ × m × v12 ] ÷ d (2)
So how do we solve for F when we don’t know the value of v1, the mug’s freefall velocity at impact? We’ll use the fact that The Law of Conservation of Energy tells us that all energies are equal, and we’ll eliminate the part of Equation (2) that contains this unknown variable, that is, the right side of the equation which deals with kinetic energy. In its place we’ll substitute terms which represent the mug’s potential energy, that is, the latent energy held within it as it sat upon the shelf prior to falling. Equation (2) then becomes,
F = [- m × g × h] ÷ d (3)
where g is the Earth’s acceleration of gravity factor, a constant equal to 9.8 meters/sec2 , and h is the height from which the mug fell.
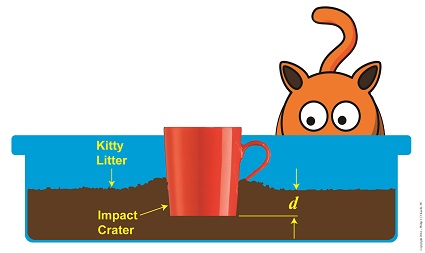
Kinetic Energy Meets With Opposing Force
So if we know the mug’s mass, the distance fallen, and the depth of the crater it made in the litter, we can determine the stopping force acting upon it at the time of impact. It’s time to plug numbers.
Let’s say our mug has a mass of 0.25 kg, it falls from a height of 2 meters, and it makes a crater 0.05 meters deep. Then the stopping force acting upon it is,
F = [- (0.25 kg) × (9.8 meters/sec2) × (2 meters)] ÷ (0.05 meters)
= – 98 Newtons
The mug was subjected to -98 Newtons, or about -22 pounds of opposing force when it fell into the litter, that resistance being presented by the litter itself.
Next time we’ll see what happens when our mug strikes a hard surface that fails to cushion its impact. Energy is released, but where does it go?
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, engineering expert, falling objects, force, kinetic energy, law of conservation of energy, mass, Newtons, potential energy, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on When Kinetic Energy Meets With Opposing Force
Thursday, February 18th, 2016
|
It’s not uncommon in my work as an engineering expert to encounter a situation in which I’m missing information. At that point I’ve got to find a creative solution to working the problem. We’ll get creative today when we combine the Law of Conservation of Energy and the Work-Energy Theorem to get around the fact that we’re missing a key quantity to calculate forces exerted upon the falling coffee mug we’ve been following in this blog series.
Last time we applied the Work-Energy Theorem to our mug as it came to rest in a pan of kitty litter. Today we’ll set up the Theorem formula to calculate the force acting upon it when it meets the litter. Here’s where we left off,
F × d = –½ × m × v12
where, F is the force acting to slow the progress of the mug with mass m inside the litter pan. The mug eventually stops and comes to rest in a crater with a depth, d. The left side of the equation represents the mug’s work expenditure, as it plows through the litter, which acts as a force acting in opposition to the mug’s travel.
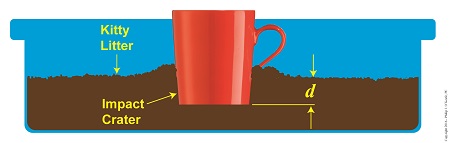
Kinetic Energy Meets Up With Displacement
The right side of the equation represents the mug’s kinetic energy, which it gained in freefall, at its point of impact with the litter. The right side is in negative terms because the mug loses energy when it meets up with this opposing force.
Let’s say we know the values for variables d and m, quantities which are easily measured. But the kinetic energy side of the equation also features a variable of unknown value, v1, the mug’s velocity upon impact. This quantity is difficult to measure without sophisticated electronic equipment, something along the lines of a radar speed detector used by traffic cops. For the purpose of our discussion we’ll say that we don’t have a cop standing nearby to measure the mug’s falling speed.
If you’ll recall from past blog discussions, the Law of Conservation of Energy states that an object’s — in this case our mug’s — kinetic energy is equal to its potential energy. It’s this equivalency relationship which will enable us to solve the equation and work around the fact that we don’t have a value for v1.
We’ll do the math and plug in the numbers next time.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: displacement, engineering expert, falling objects, impact force, kinetic energy, law of conservation of energy, mass, opposing force, potential energy, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Combining the Law of Conservation of Energy and Work-Energy Theorem
Monday, February 8th, 2016
|
So far we’ve applied the Work-Energy Theorem to a flying object, namely, Santa’s sleigh, and a rolling object, namely, a car braking to avoid hitting a deer. Today we’ll apply the Theorem to a falling object, that coffee mug we’ve been following through this blog series. We’ll use the Theorem to find the force generated on the mug when it falls into a pan of kitty litter. This falling object scenario is one I frequently encounter as an engineering expert, and it’s something I’ve got to consider when designing objects that must withstand impact forces if they are dropped.

Applying the Work-Energy Theorem to Falling Objects
Here’s the Work-Energy Theorem formula again,
F × d = ½ × m × [v22 – v12]
where F is the force applied to a moving object of mass m to get it to change from a velocity of v1 to v2 over a distance, d.
As we follow our falling mug from its shelf, its mass, m, eventually comes into contact with an opposing force, F, which will alter its velocity when it hits the floor, or in this case a strategically placed pan of kitty litter. Upon hitting the litter, the force of the mug’s falling velocity, or speed, causes the mug to burrow into the litter to a depth of d. The mug’s speed the instant before it hits the ground is v1, and its final velocity when it comes to a full stop inside the litter is v2, or zero.
Inserting these values into the Theorem, we get,
F × d = ½ × m × [0 – v12]
F × d = – ½ × m × v12
The right side of the equation represents the kinetic energy that the mug acquired while in freefall. This energy will be transformed into Gaspard Gustave de Coriolis’ definition of work, which produces a depression in the litter due to the force of the plummeting mug. Work is represented on the left side of the equal sign.
Now a problem arises with using the equation if we’re unable to measure the mug’s initial velocity, v1. But there’s a way around that, which we’ll discover next time when we put the Law of Conservation of Energy to work for us to do just that.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: energy, engineering expert, falling objects, Gaspard-Gustave de Coriolis, impact forces, kinetic energy, law of conservation of energy, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury | Comments Off on Applying the Work-Energy Theorem to Falling Objects
Friday, January 1st, 2016
|
As an engineering expert I’ve applied the Work-Energy Theorem to diverse situations, but none as unique as its most recent application, the progress of Santa’s sleigh. Last week we saw how Santa and his reindeer team encountered a wind gust which generated enough force to slow them from an initial velocity of v1 to a final velocity, v2, over a distance, d. Today we’ll begin using the Work-Energy Theorem to see if Santa was able to keep to his Christmas delivery schedule and get all the good boys and girls their gifts in time.

Before we can work with the Work-Energy Theorem, we must first revisit the formula it’s predicated upon, de Coriolis’ formula for kinetic energy,
KE = ½ × m × v2 (1)
where, KE is kinetic energy, m is the moving object’s mass, and v its velocity.
The equation behind the Work-Energy Theorem is,
W = KE2 – KE1 (2)
where W is the work performed, KE1 is the moving object’s initial kinetic energy and KE2 its final kinetic energy after it has slowed or stopped. In cases where the object has come to a complete stop KE2 is equal to zero, since the velocity of a stationary object is zero.
In order to work with equation (2) we must first expand it into a more useful format that quantifies an object’s mass and initial and final velocities. We’ll do that by substituting equation (1) into equation (2). The result of that term substitution is,
W = [½ × m × v22 ] – [½ × m × v12] (3)
Factoring out like terms, equation (3) is simplified to,
W = ½ × m × [v22 – v12] (4)
Now according to de Coriolis, work is equal to force, F, times distance, d. So substituting these terms for W in equation (4), the expanded version of the Work-Energy Theorem becomes,
F × d = ½ × m × [v22 – v12] (5)
Next time we’ll apply equation (5) to Santa’s delivery flight to calculate the strength of that gust of wind slowing him down.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis, distance, energy, engineering expert, force, kinetic energy, mass, velocity, wind force, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury | Comments Off on The Math Behind the Work-Energy Theorem
Friday, December 18th, 2015
|
My work as an engineering expert sometimes involves computations of energy expended, as when I must determine how much energy is required to move something. But sometimes the opposite needs to be calculated, that is, how much energy is required to stop something already in motion. That’s the subject of today’s discussion, which we’ll approach by way of the Work-Energy Theorem.
The Work-Energy Theorem states that the work required to slow or stop a moving object is equal to the change in energy the object experiences while in motion, that is, how its kinetic energy is reduced or completely exhausted. Although we don’t know who to attribute the Theorem to specifically, we do know it’s based on the previous work of Gaspard Gustave de Coriolis and James Prescott Joule, whose work in turn built upon that of Isaac Newton’s Second Law of Motion.
Consider the example shown here. A ball of mass m moves unimpeded through space at a velocity of v1 until it is met by an opposing force, F. This force acts upon the ball over a travel distance d, resulting in the ball’s slowing to a velocity of v2.
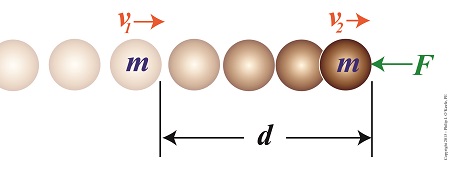
The Work – Energy Theorem Illustrated
Does the illustration make clear the Work-Energy Theorem dynamics at play? If not, return for the second part of this blog, where we’ll clarify things by getting into the math behind the action.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: energy, engineering expert witness, Gaspard-Gustave de Coriolis, Isaac Newton's Second Law of Motion, James Prescott Joule, kinetic energy, moving object, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Work-Energy Theorem — Background