|
In this blog series we’ve been working our way towards determining mass values for heavenly bodies in our universe. Today we’ll explore the inverse relationship phenomenon that’s present when examining the acceleration of gravity between two heavenly bodies, for our purposes Earth and its moon. To demonstrate the inverse relationship phenomenon, we’ll use Newton’s Law of Gravitation formula: g = (G × M) ÷ r2 (1) In this formula g represents Earth’s acceleration of gravity that’s acting upon the moon. The center of the moon is located at a distance r from Earth’s center. Earth’s mass is represented by M, and G is the universal gravitational constant, which never varies from its value of 3.49 × 10-8 cubic feet per slug per second squared. We’ll solve for Earth’s g factor relative to the moon, which we’ll position at varying distances from Earth’s core, thereby demonstrating how the attracting force of Earth’s gravity becomes weaker as the moon’s distance from Earth’s core increases — hence the inverse relationship. To begin, we know that the present distance from Earth’s center to the center of the moon is about 238,900 miles, or 1,261,392,000 feet. We also know that Earth’s mass, M, is equal to 4.09 × 1023 slugs. Plugging these values into Newton’s Law of Gravitation equation, we calculate the acceleration of gravity exerted upon the moon in this, its normal orbit, to be: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (1,261,392,000 ft)2 g = 0.0089 ft/sec2 Now let’s suppose that the moon’s orbit was caused to increase so that it became situated 400,000 miles, or 2,112,000,000 feet from Earth. Earth’s acceleration of gravity exerted upon the moon at this distance would be calculated as: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (2,112,000,000 ft)2 g = 0.0032 ft/sec2 From these two examples we can see that the further the moon is positioned from Earth, the weaker Earth’s gravitational pull upon it is. This gravitational pull is the force of gravity, Fg, introduced in our last blog, a term which originates in Newton’s Second Law of Motion, as given by the equation: Fg = m × g (2) where, in this case, m represents the mass of the moon. Next time we’ll combine equations (1) and (2) and derive a third formula which will allow us to calculate the mass of the sun.
_______________________________________
|
Posts Tagged ‘mass’
The Inverse Relationship of the Acceleration of Gravity
Friday, December 5th, 2014The Force of Gravity
Thursday, November 20th, 2014|
Last time we saw how Henry Cavendish built upon the work of scientists before him to calculate Earth’s mass and its acceleration of gravity factor, as well as the universal gravitational constant. These values, together with the force of gravity value, Fg, which we’ll introduce today, moved scientists one step further towards being able to discover the mass and gravity of any heavenly body in the universe. According to Newton’s Second Law of Motion, the force of gravity, Fg, acting upon any object is equal to the object’s mass, m, times the acceleration of gravity factor, g, or, Fg = m × g So what is Fg? It’s a force at play way up there, in the outer reaches of the galaxy, as well as back home. It keeps the moon in orbit around the Earth and the Earth orbiting around the sun. In the same way, Fg keeps us anchored to Earth, and if we were to calculate it, it would be calculated as the force of our body’s mass under the influence of Earth’s gravity. It’s common to refer to this force as weight, but it’s not quite so simple. Using the metric system, the unit of measurement most often used for scientific analyses, weight is determined by multiplying our body’s mass in kilograms by the Earth’s acceleration of gravity factor of 9.8 meters per second per second, or 9.8 meters per second squared. For example, suppose your mass is 100 kilograms. Your weight on Earth would be: Weight = Fg = m × g = (100 kg) × (9.8 m/sec2) = 980 kg · m/sec2 = 980 Newtons Newtons? That’s right. It’s easier than saying kilogram · meter per second per second. It’s also a way to pay homage to the man himself. In the English system of measurement things are perhaps even more confusing. Your weight is found by multiplying the mass of your body measured in slugs by the Earth’s acceleration of gravity factor of 32 feet per second per second. Slugs is British English speak for pounds · second squared per foot. We normally refer to weight in units of pounds, and in engineering circles it’s pounds force. For example, suppose your mass is 6 slugs, or 6 pounds · second squared per foot. Your weight on Earth would be: Weight = Fg = m × g = (6 Lbs · sec2/ft) × (32.2 ft/sec2)= 193.2 Lbs To avoid any confusion, you could just step on the bathroom scale. Next time we’ll see how the force of gravity is influenced by an inverse proportionality phenomenon. _______________________________________
|
Proving Galileo’s Theory On Falling Objects
Thursday, September 11th, 2014|
Last time we discussed how Galileo proved Aristotle’s theory regarding the physics of falling objects to be wrong, although his experiment, which took place on the infamous Leaning Tower of Pisa, did not actually prove his own theory to be correct. So why didn’t Galileo go the extra mile and prove his theory? Because he couldn’t. Galileo, of course, resided on Earth, which was also the arena in which his experiment took place. As such, both he and his experiment were subject to the physical constraints presented by the Earth lab, the single most influential factor being the impact of the planet’s atmosphere upon his falling objects. Put another way, contrary to popular belief at the time, air is not an empty, innocuous space devoid of physical properties. It’s actually a gaseous soup of molecules. Nitrogen, oxygen, carbon, hydrogen, and other elements are in the mix, and they all have mass, that is, weight within a gravitational field. As Galileo’s balls fell, they continuously bumped against these molecules, which slowed their descent. This air friction will be discussed later in our blog series. But in order to prove Galileo’s theory correct beyond a shadow of a doubt, the testing arena would need to be one free from the interference of atmosphere. The Moon fits this criterion and provided the perfect environment to prove, once and for all, that Galileo’s theory was correct. So when astronauts Scott and Irwin simultaneously dropped a hammer and feather to the Moon’s surface, both objects hit at precisely the same moment. Watch this captured live footage of the event to see for yourself: One thing you may have noticed while watching the astronauts’ experiment is that the hammer fell more slowly than it would have on Earth. This has nothing to do with the absence of atmosphere on the Moon, but it has everything to do with gravity. We’ll discuss gravity’s influence in detail next time. _______________________________________
|
Mechanical Power Transmission – Centrifugal Force and Centrifugal Clutches
Monday, April 9th, 2012| I’m not a big fan of amusement parks. The first time I rode on a Tilt-A-Whirl I was caught off guard and flung onto my side by the centrifugal force acting upon my body, the lower half of which was constrained by a seat belt so I wouldn’t be catapulted out during the ride. To make matters worse, the centrifugal force started to force the lunch I’d made the mistake of eating just before back up my throat. It was a very unpleasant experience to say the least.
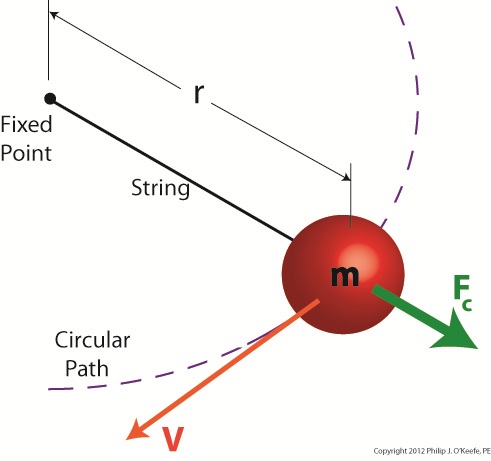
Centrifugal force is an interesting phenomenon, and its principles are involved in the operation of a centrifugal clutch, which we’ll see later. For now, let’s get a basic understanding of what it’s all about, thanks to the discoveries of Sir Isaac Newton in the late 17th Century. Figure 1
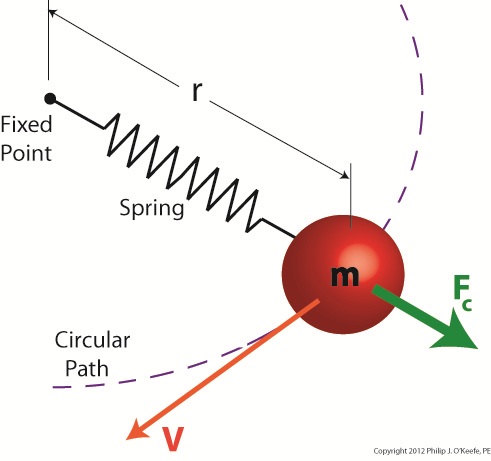
Figure 1 shows a red ball, whose mass we’ll notate m, attached to a string, the other end of which is attached to a fixed point, such as if you held it taught between your fingers. If you’re in a playful mood, you might enjoy twirling the ball above your head on its string. The distance between the center of the ball and the fixed point is labeled r, which stands for the radius of the circular path traveled by the ball as it twirls around the fixed point. The speed at which the ball travels through the air is called its straight line velocity, or tangential velocity in scientific-speak, and it is generally notated as a V. The centrifugal force, or Fc, that is exerted upon the ball as it whirls around your head is, Sir Isaac tells us, measured by the equation: Fc = mV2/r Centrifugal force in the simplest of terms is an outward-pushing force that pulls objects in motion away from the point about which they’re rotating. Let’s hold as fact that if m and r don’t change, then Newton’s equation tells us that the centrifugal force exerted upon the object in motion increases by the square of the velocity, or speed, of the ball. In other words, the faster the ball moves as you spin it around your head on the string, the harder the centrifugal force that acts upon it. As you spin the ball faster and faster, it will pull outward more and more strenuously, exerting ever greater resistance upon the string you hold between your fingers. Now suppose we replace the string in this example with a spring as shown in Figure 2. Figure 2
Why a spring? Because that’s what’s used within a centrifugal clutch. Just as with the string, the ball’s velocity increases as you increase rotation speed around the fixed point, and the centrifugal force acting upon its mass by the spinning action increases as well. The spring expands, extending further and further out from its beginning position of attachment to the fixed point, your fingers. As velocity decreases, the spring will retract, eventually returning to its original coil size. This extending and retracting action is the major mechanism at play within a centrifugal clutch. Next time we’ll explore a centrifugal clutch mechanism in more depth to observe its behavior relative to its spring under the influence of centrifugal force. ____________________________________________
|