|
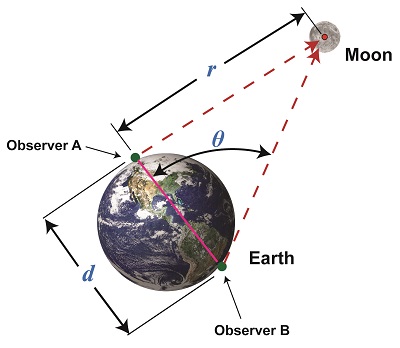
Last time we learned that the bigger an optical rangefinder, the better its accuracy in measuring distant objects. Today we’ll take that concept a step further when we discover how Earth itself was used by ancient scientists to gauge its distance to the moon. Today’s blog will be strewn with embedded links to past blogs in this series, all of which have been building up to our understanding of gravity, a complex subject with many pieces to its puzzle. There are a few remaining pieces to be placed which will be covered in future blogs, but I promise we’ll get there. Long before Edmund Halley’s time, scientists used the Earth as a huge optical rangefinder. In doing so they employed the principles of parallax and trigonometry to obtain reasonably accurate measurements of the distance between Earth and its nearest neighbors, starting with the moon. See Figure 1. The illustration shows how it was done. Two observers armed with telescopes viewed the moon from opposite sides of the earth. Their lines of sight are represented by dashed lines, and together with the solid pink line which represents the distance between them, d, a right triangle was formed. Because Observer B was situated on the other side of the globe, his line of sight fell at an angle relative to Observer A’s, due to the Principle of Parallax. The angle that formed at the point in the triangle at which B was situated we’ll call θ. The fact that a right triangle was formed at Observer A’s observation point will enable our ancient scientists to use principles of trigonometry and parallax in their quest to find the distance to the moon. Follow this link to a refresher blog on the subject, Using Parallax to Measure Distance. At precisely the same moment the moon moved into Observer A’s telescopic line of sight, Observer B adjusted his telescope to center the moon within it. Observer B then duly measured the angle θ formed with a protractor, just as would be done with a rangefinder. If you’ve been reading along in this series, this setup might look familiar to you. In fact, the two mirrors of a military optical rangefinder work in exactly the same way as our two observers looking at the moon. Follow this link to a refresher on the internal workings of a rangefinder. Once the angle θ’s value had been determined, it was used to calculate the distance r between Earth and the moon with the same equation we’ve been using to measure distances using military optical rangefinders: r = d × tan(θ) As far as our moon observers go, the only variable left for them to determine before they are able to measure Earth’s distance to the moon is d, the distance between their viewing positions on Earth. We’ll see how to solve for d next time, when we put the Earth’s geometry to work for us.
____________________________________
|
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE