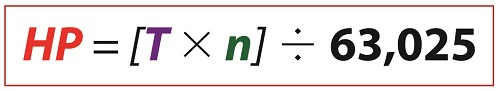Posts Tagged ‘moment of inertia’

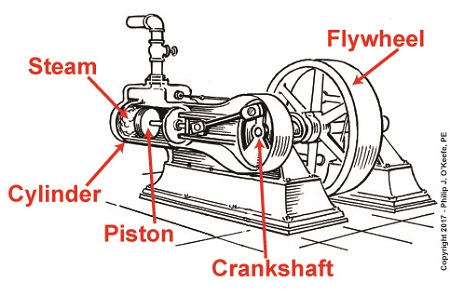
Reciprocating Engines Maximize Efficiency When They Employ Flywheels

Thursday, December 21st, 2017

   Last time we had a look inside a marvelous piece of engineering machinery known as a crankshaft.   It plays a key role in converting the reciprocating linear motion of a steam driven engine into the rotary motion required to power externally mounted devices that are attached to it.   Today we’ll finish up our blog series on flywheels when we see how using one in conjunction with a crankshaft facilitates a more even transmission of energy.   Reciprocating engines maximize efficiency when they employ flywheels.

   We learned that the energy in the steam supply decreases as the piston moves in its cylinder, which means a concurrent decrease in the engine’s horsepower and its ability to power machinery.   Without an intervening action, the reciprocating steam engine would stall.   Now, let’s see how adding a flywheel to the crankshaft can solve the problem.

Reciprocating Engines Maximize Efficiency When They Employ Flywheels

Reciprocating Engines Maximize Efficiency When They Employ Flywheels

   

   As we’ve learned before, a flywheel stores up kinetic energy while the engine powering it is performing at full horsepower, but if that power should drop off or cease to be produced, the flywheel gives up the kinetic energy stored inside it so as to keep externally mounted machinery operating until that stored energy is exhausted.   This is all made possible because flywheels are designed to have moments of inertia sufficient to positively contribute to its storage of kinetic energy.   This inertia is a numerical representation of the flywheel’s resistance to change in motion.   Please review our past blog on the subject to refresh your memory.

   The overall effect is that while the engine is operating, there’s an even flow of energy between the engine and flywheel and horsepower is supplied to keep machinery mounted to the crankshaft operating.   Any diminishment in the power supplied will be compensated for by the flywheel’s stored kinetic energy.

   Next time we’ll introduce a new topic, a phenomenon known as cavitation.

opyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Reciprocating Engines Maximize Efficiency When They Employ Flywheels

Horsepower Required to Accelerate a Flywheel

Friday, November 24th, 2017

    Last time we discussed how torque is created as a flywheel spins.   This torque is a factor of the flywheel’s moment of inertia, which is dependent on how far the masses of the flywheel’s parts are located from its center of rotation.   Today we’ll present a formula to compute how much horsepower is required to accelerate a flywheel.   And here it is,

Horsepower Required to Accelerate a Flywheel

Horsepower Required to Accelerate a Flywheel

where, T is the torque created on the flywheel’s shaft in units of inch-pounds.   The term n is the flywheel shaft’s speed of rotation in revolutions per minute, RPM.   Horsepower, HP, is engineering shorthand for a unit of power equal to 6600 inch-pounds per second, and the number 63,025 is a constant needed to convert torque, T, and the spinning shaft’s rotations per minute, RPM, into horsepower units.

    Torque is present whether the flywheel’s spin accelerates or decelerates.   During acceleration torque is created, which contributes to the production of kinetic energy that’s stored inside the flywheel.  When a flywheel’s spin decelerates, its mass experiences the effects of negative acceleration, and stored kinetic energy is released.

    As we learned awhile back, horsepower is a function of torque in any moving machinery, including engines and flywheels.  An engine must produce horsepower to accelerate a flywheel connected to its shaft.   By the same token, when the engine’s horsepower output diminishes or stops, the flywheel begins to decelerate.   This deceleration causes kinetic energy stored within the flywheel to be released, providing horsepower necessary to keep the engine and flywheel spinning.   That is, until the power output of the engine returns or the stored kinetic energy of the flywheel is ultimately exhausted.

    We’ll see how that works next time when we take a look inside a reciprocating engine.

opyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Horsepower Required to Accelerate a Flywheel

Flywheel Torque and Distribution of Mass

Monday, November 13th, 2017

    Last time we began our discussion on moment of inertia and how it affects a flywheel’s storage of kinetic energy.   That inertia is a function of the flywheel’s mass, in particular how the mass is distributed.   Today we’ll continue our discussion and see how an engineering principal known as torque affects things.

Flywheel Torque and Distribution of Mass

Flywheel Torque and Distribution of Mass

   

    We learned in a previous blog that torque is most simply defined as a measure of how much force acts upon an object to cause it to rotate around a pivot point or center of rotation, shown as a small black dot in the illustration.   For our discussion we’ll focus on two parts of the flywheel, the hub, part A, and the rim, part E.

    Part A has a mass mA located a distance rA from the flywheel’s center, while part E has a mass mE located a distance rE from it.   When an engine applies mechanical power to the flywheel by way of its rotating shaft, the revolutions per minute, RPM, increase and along with it the angular velocity, ω, also increases.   For a refresher on this, follow the link.

    Because of this relationship, we can calculate the kinetic energy contained within a flywheel using the kinetic energy formula,

KE = ½ × ∑[m × r2] × ω2               (1)

    As the flywheel’s angular velocity increases or decreases in response to the engine’s energy output, parts A and E reflect acceleration or deceleration of aA and aE.   Since parts A and E exhibit both mass and acceleration, they are subject to Newton’s Second Law of Motion, which states that force equals mass times acceleration.   Using that relationship we can calculate the force exerted on each part by,

FA = mA ×  aA                                  (2)

FE = mE ×  aE                                  (3)

    Part A is small compared to part E, therefore mE is greater than mA and accordingly FE is greater than FA.   Forces FA and FE act as torques, because they cause parts A and E to rotate around the flywheel’s center of rotation, so they are designated as Torque A, TA, and Torque E, TE.    These torques are computed by,

TA = FA ×  rA                                   (4)

TE = FE ×  rE                                   (5)

    Part E’s greater mass will contribute more torque than part A, and it will also contribute more to the flywheel’s kinetic energy content.

    Most flywheels are designed with heavy rims supported by small hubs and slender spokes, because the more mass that’s distributed away from the flywheel’s center of rotation, the greater the flywheel’s moment of inertia and torque, and the more kinetic energy it can store.

    Next time we’ll develop an equation which allows us to quantify the horsepower required to accelerate a flywheel.

opyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Flywheel Torque and Distribution of Mass

Moment of Inertia in a Flywheel

Monday, November 6th, 2017

    Last time we arrived at a general formula to compute the kinetic energy, KE, contained within the totality of a spinning flywheel made up of numerous parts.   Today we’ll discuss the terms in that formula, which encompasses a phenomenon of flywheels known as moment of inertia.

Moment of Inertia in a Flywheel

Moment of Inertia in a Flywheel

   

   The kinetic energy formula we’ve been working with is, again,

KE = ½ × Σ[m × r2] × ω2                           (1)

    The bracketed part of this equation makes reference to spinning flywheels comprised of one or more parts, and that’s what we’ll be focusing on today.   The symbol Σ is the Greek letter sigma, standard engineering shorthand notation used to represent the sum of all terms and mathematical operations contained within the brackets.

    Our illustration shows we have five parts to consider:  a hub, three spokes and a rim, and label them A, B, C, D, and E respectively.   Each part has its own mass, m, and is a unique distance, r, from the flywheel’s center of rotation.   The flywheel’s angular velocity is represented by ω.

   For our flywheel of parts A through E our expanded equation becomes,

Σ[m × r2] = [mA × rA2] + [mB × rB2] + [mC × rC2] + [mD × rD2] + [mE × rE2]      (2)

    Equation (2) represents the sum total of moments of inertia contained within our flywheel.  It’s a numerical representation of the flywheel’s degree of resistance to changes in motion.

    The more mass a flywheel has, the greater its moment of inertia.  When at rest this greater moment of inertia means it will take more effort to return it to motion.   But once in motion the flywheel’s greater moment of inertia will make it harder to stop.   That’s because there’s a lot of kinetic energy stored within its spinning mass, and the heavier a flywheel is, the more kinetic energy it contains.   In fact, for any given angular velocity ω, a large and heavy flywheel stores more kinetic energy than a smaller, lighter flywheel.

    But there’s more to a flywheel’s moment of inertia than just mass.   What’s really important is how that mass is distributed. We’ll get into that next time when we discuss torque.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Moment of Inertia in a Flywheel

How Much Kinetic Energy is Contained Within a Spinning Flywheel?

Thursday, October 26th, 2017

    Last time we introduced the fact that spinning flywheels are subject to both linear and angular velocities, along with a formula that allows us to calculate these quantities for a single part of the flywheel, designated A.   We also re-visited the kinetic energy formula.   Today we’ll build upon those formulas as we attempt to answer the question, How much kinetic energy is contained within a spinning flywheel?

    Here again is the basic kinetic energy formula,

KE = ½ × m × v2                                                                (1)

where, m equals a moving object’s mass and v is its linear velocity.

    Here again is the formula used to calculate linear and angular velocities for a single part A within the flywheel, where part A’s linear velocity is designated vA,  angular velocity by ω, and where rA is the distance of part A from the flywheel’s center of rotation.

vA = rA × ω                                                                         (2)

    Working with these two formulas, we’ll insert equation (2) into equation (1) to obtain a kinetic energy formula which allows us to calculate the amount of energy contained in part A of the flywheel,

KEA = ½ × mA × (rA × ω)2                                                 (3)

which simplifies to,

KEA = ½ × mA ×  rA2  ×  ω2                                              (4)

    Equation (4) is a great place to begin to calculate the amount of kinetic energy contained within a spinning flywheel, however it is just a beginning, because a flywheel contains many parts.  Each of those parts has its own mass, m, and is a unique distance, r, from the flywheel’s center of rotation, and all these parts must be accounted for in order to arrive at a calculation for the total amount of kinetic energy contained within a spinning flywheel.

How Much Kinetic Energy is Contained Within a Spinning Flywheel?

How Much Kinetic Energy is Contained Within a Spinning Flywheel?

   

    Put another way, we must add together all the m × r2 terms for each and every part of the entire flywheel.   How many parts are we speaking of?  Well, that depends on the type of flywheel.  We’ll discuss that in detail later, after we define a phenomenon that influences the kinetic energy of a flywheel known as the moment of inertia.

    For now, let’s just consider the flywheel’s parts in general terms.  A general formula to compute the kinetic energy contained within the totality of a spinning flywheel is,

KE = ½ × ∑[m × r2] × ω2                                                  (5)

    We’ll discuss the significance of each of these variables next time when we arrive at a method to calculate the kinetic energy contained within all the many parts of a spinning flywheel

.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on How Much Kinetic Energy is Contained Within a Spinning Flywheel?

Two Types of Velocity Associated With a Spinning Flywheel

Thursday, October 19th, 2017

    Anyone who has spun a potter’s wheel is appreciative of the smooth motion of the flywheel upon which they form their clay, for without it the bowl they’re forming would display irregularities such as unattractive bumps.   The flywheel’s smooth action comes as a result of kinetic energy, the energy of motion, stored within it.   We’ll take another step towards examining this phenomenon today when we take our first look at calculating this kinetic energy.   To do so we’ll make reference to the two types of velocity associated with a spinning flywheel, angular velocity and linear velocity, both of which engineers must negotiate anytime they deal with rotating objects.

    Let’s begin by referring back to the formula for calculating kinetic energy, KE.  This formula applies to all objects moving in a linear fashion, that is to say, traveling a straight path.   Here it is again,

KE = ½ × m × v2

where m is the moving object’s mass and v its linear velocity.

    Flywheels rotate about a fixed point rather than move in a straight line, but determining the amount of kinetic energy stored within a spinning flywheel involves an examination of both its angular velocity and linear velocity.   In fact, the amount of kinetic energy stored within it depends on how fast it rotates.

    For our example we’ll consider a spinning flywheel, which is basically a solid disc.   For our illustrative purposes we’ll divide this disc into hypothetical parts, each having a mass m located a distance r from the flywheel’s center of rotation.   We’ll select a single part to examine and call that A.

Two Types of Velocity Associated With a Spinning Flywheel

Two Types of Velocity Associated With a Spinning Flywheel

   

    Part A has a mass, mA, and is located a distance rA from the flywheel’s center of rotation.   As the flywheel spins, part A rides along with it at an angular velocity, ω, following a circular path, shown in green.   It also moves at a linear velocity, vA, shown in red.   vA represents the linear velocity of part A measured at any point tangent to its circular path.  This linear velocity would become evident if part A were to become disengaged from the flywheel and cast into the air, whereupon its trajectory would follow a straight line tangent to its circular path.

    The linear and angular velocities of part A are related by the formula,

vA = rA × ω

    Next time we’ll use this equation to modify the basic kinetic energy formula so that it’s placed into terms that relate to a flywheel’s angular velocity.   This will allow us to define a phenomenon at play in the flywheel’s rotation, known as the moment of inertia.

 

 

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Two Types of Velocity Associated With a Spinning Flywheel