|
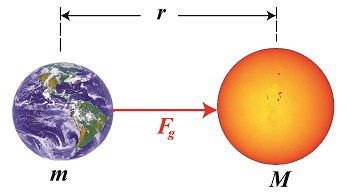
As a young school boy I found it hard to believe that scientists were able to compute the mass of our sun. After all, a galactic-sized measuring device does not exist. But where there’s a will, there’s a way, and by the 18th Century scientists had it all figured out, thanks to the work of others before them. Newton’s two formulas concerning gravity were key to later scientific discoveries, and we’ll be working with them again today to derive a third formula, bringing us a step closer to determining our sun’s mass. Newton’s Second Law of Motion allows us to compute the force of gravity, Fg, acting upon the Earth, which has a mass of m. It is, Fg = m × g (1) Newton’s Universal Law of Gravitation allows us to solve for g, the sun’s acceleration of gravity value, g = (G × M) ÷ r2 (2) where, M is the mass of the sun, r is the distance between the sun and Earth, and G is the universal gravitational constant. You will note that g is a common factor between the two equations, and we’ll use that fact to combine them. We’ll do so by substituting the right side of equation (2) for the g in equation (1) to get, Fg = m × [(G × M) ÷ r2] then, using algebra to rearrange terms, we’ll set up the combined equation to solve for M, the sun’s mass: M = (Fg × r2) ÷ (m × G) (3) At this point in the process we know some values for factors in equation (3), but not others. Thanks to Henry Cavendish’s work we know the value of m, the Earth’s mass, and G, the universal gravitational constant. What we don’t yet know is Earth’s distance to the sun, r, and the gravitational attractive force, Fg, that exists between them. Next time we’ll introduce some key scientists whose work contributed to a method for computing the distance of our planet Earth to its sun. _______________________________________
|
Posts Tagged ‘Newton’s Second Law of Motion’
Gravity and the Mass of the Sun
Friday, December 12th, 2014The Inverse Relationship of the Acceleration of Gravity
Friday, December 5th, 2014|
In this blog series we’ve been working our way towards determining mass values for heavenly bodies in our universe. Today we’ll explore the inverse relationship phenomenon that’s present when examining the acceleration of gravity between two heavenly bodies, for our purposes Earth and its moon. To demonstrate the inverse relationship phenomenon, we’ll use Newton’s Law of Gravitation formula: g = (G × M) ÷ r2 (1) In this formula g represents Earth’s acceleration of gravity that’s acting upon the moon. The center of the moon is located at a distance r from Earth’s center. Earth’s mass is represented by M, and G is the universal gravitational constant, which never varies from its value of 3.49 × 10-8 cubic feet per slug per second squared. We’ll solve for Earth’s g factor relative to the moon, which we’ll position at varying distances from Earth’s core, thereby demonstrating how the attracting force of Earth’s gravity becomes weaker as the moon’s distance from Earth’s core increases — hence the inverse relationship. To begin, we know that the present distance from Earth’s center to the center of the moon is about 238,900 miles, or 1,261,392,000 feet. We also know that Earth’s mass, M, is equal to 4.09 × 1023 slugs. Plugging these values into Newton’s Law of Gravitation equation, we calculate the acceleration of gravity exerted upon the moon in this, its normal orbit, to be: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (1,261,392,000 ft)2 g = 0.0089 ft/sec2 Now let’s suppose that the moon’s orbit was caused to increase so that it became situated 400,000 miles, or 2,112,000,000 feet from Earth. Earth’s acceleration of gravity exerted upon the moon at this distance would be calculated as: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (2,112,000,000 ft)2 g = 0.0032 ft/sec2 From these two examples we can see that the further the moon is positioned from Earth, the weaker Earth’s gravitational pull upon it is. This gravitational pull is the force of gravity, Fg, introduced in our last blog, a term which originates in Newton’s Second Law of Motion, as given by the equation: Fg = m × g (2) where, in this case, m represents the mass of the moon. Next time we’ll combine equations (1) and (2) and derive a third formula which will allow us to calculate the mass of the sun.
_______________________________________
|