|
Hold onto your hats, we’re going to deal with a lot of equations today! Last time we used flashbacks to previous blogs in this series to revisit key equations in our ongoing discussion of gear trains and torque. We also introduced The Law of Conservation of Energy in conjunction with five equations that together demonstrate how when increasing torque by use of a simple gear train, we do so at the cost of speed. Those five equations are:
where, R is the gear ratio, N the number of gear teeth, n the gear’s rotational speed, T the torque, D the gear pitch radius, and HP is the horsepower transmitted by the gears. As we work the equations, keep in mind that our ultimate objective is to find a way to link together (1) and (2), the equations dealing with gear torque and speed. Once we accomplish this we’ll see how increased torque is obtained at the cost of speed. But because there are no common terms between equations (1) and (2), our first step is to develop one. Developing a link between equations (1) and (2) is a process that begins with combining equations (2), (3), and (4).
The common terms in these three equations are TDriving and TDriven, so we’ll manipulate things in order to group them together. We’ll substitute equation (3) for the TDriving term in equation (2), and substitute equation (4) for the TDriven term in equation (2). We are now able to link all three equations to get: {[HPDriving ÷ nDriving] × 63,025} ÷ {[HPDriven ÷ nDriven] × 63,025} = DDriving ÷ DDriven (6) Now let’s go a step further to simplify equation (6). From equation (5) we know that the driving and driven gear horsepowers are equal. So, in equation (6), the HPDriving and HPDriven cancel out, along with the two 63,025 terms, allowing us to arrive at equation (7): {[HPDriving ÷ nDriving] × 63,025} ÷ {[HPDriven ÷ nDriven] × 63,025} = DDriving ÷ DDriven
Next week we’ll use equation (7) to link together R, N, n, of equation (1) with D and T of equation (2) and in so doing disclose mathematically the tradeoff between torque and speed, then apply our findings to an example. _______________________________________
|
Posts Tagged ‘number of teeth’
Determining the Gear Train Tradeoff of Torque vs. Speed, Part One
Friday, August 15th, 2014Gear Ratio Formulas
Sunday, February 23rd, 2014|
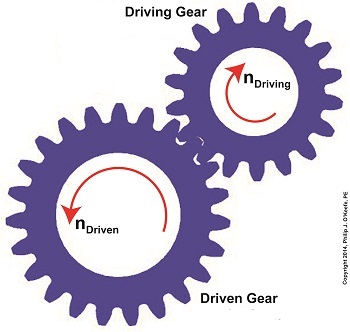
Last time we introduced a way to convert individual gear speeds in relation to one another within a gear train by employing a conversion tool known as the gear ratio. Today we’ll introduce the gear ratio formulas, of which there are two types. The first formula for determining gear ratio is based on knowing the driving gear revolutions per minute (RPM), notated as nDriving, and the driven gear RPM, nDriven. Given that knowledge we can calculate the gear ratio, R, that exists between them by the formula: R = nDriving ÷ nDriven (1) The other way to determine gear ratio, R, is by knowing the number of teeth on both the driving gear, NDriving, and the driven gear, NDriven. That’s right, it all boils down to simply counting the number of teeth on each gear. In this instance the gear ratio is calculated by the following formula: R = NDriven ÷ NDriving (2) Equations (1) and (2) may look virtually identical, but they’re not. In mechanical engineering calculations, lower case n is typically used to denote the RPM of rotating objects such as shafts, wheels, pulleys, and gears. Upper case N is typically used to denote the number of teeth on a gear. Next time we’ll see how to manipulate these two equations so as to arrive at a particular gear ratio. _______________________________________ |