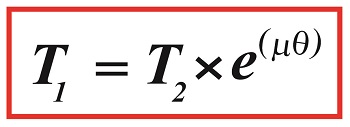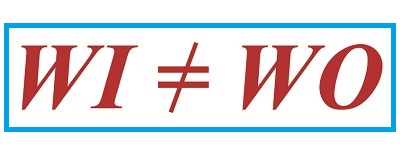Posts Tagged ‘pulley’
Sunday, June 4th, 2017
|
We’ve been talking about pulleys for awhile now, and last week we introduced the term friction coefficient, numerical values derived during testing which quantify the amount of friction present when different materials interact. Friction coefficients for common materials are routinely presented in engineering texts like Marks’ Standard Handbook for Mechanical Engineers. But there are circumstances when more specificity is required, such as when the U.S. Navy, more specifically the Navy Material Command, tested the interaction between various synthetic ropes and ship capstans and developed their own specialized friction coefficients in the process.

Navy Capstans and the Development of Specialized Friction Coefficients
Capstans are similar to pulleys but have one key difference, they’re made so rope can be wound around them multiple times. When the Navy set out to determine which synthetic rope worked best with their capstans, they did testing and developed highly specialized friction coefficients in the process. This research was at one time Top Secret but has now been declassified. To read more about it, follow this link to the actual handbook:
https://archive.org/stream/DTIC_ADA036718#page/n0/mode/2up
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: capstan, engineering, friction, friction coefficient, pulley, rope
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Navy Capstans and the Development of Specialized Friction Coefficients
Sunday, May 14th, 2017
|
Last time we introduced some of the variables in the Euler-Eytelwein Formula, an equation used to examine the amount of friction present in pulley-belt assemblies. Today we’ll explore its two tension-denoting variables, T1 and T2.
Here again is the Euler-Eytelwin Formula,where, T1 and T2 are belt tensions on either side of a pulley,
T1 = T2 × e(μθ)
T1 is known as the tight side tension of the assembly because, as its name implies, the side of the belt containing this tension is tight, and that is so due to its role in transmitting mechanical power between the driving and driven pulleys. T2 is the loose side tension because on its side of the pulley no mechanical power is transmitted, therefore it’s slack–it’s just going along for the ride between the driving and driven pulleys.
Due to these different roles, the tension in T1 is greater than it is in T2.
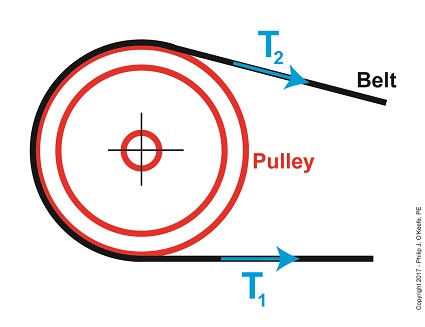
The Two T’s of the Euler-Eytelwein Formula
In the illustration above, tension forces T1 and T2 are shown moving in the same direction, because the force that keeps the belt taught around the pulley moves outward and away from the center of the pulley.
According to the Euler-Eytelwein Formula, T1 is equal to a combination of factors: tension T2 ; the friction that exists between the belt and pulley, denoted as μ; and how much of the belt is in contact with the pulley, namely θ.
We’ll get into those remaining variables next time.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, belt tension, driven pulley, driving pulley, engineering, Euler-Eytelwein Formula, mechanical power transmission, pulley
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Two T’s of the Euler-Eytelwein Formula
Friday, May 5th, 2017
|
Last time we introduced the Pulley Speed Ratio Formula, a Formula which assumes a certain amount of friction in a pulley-belt assembly in order to work. Today we’ll introduce another Formula, one which oversees how friction comes into play between belts and pulleys, the Euler-Eytelwein Formula. It’s a Formula developed by two pioneers of engineering introduced in an earlier blog, Leonhard Euler and Johann Albert Eytelwein.
Here again is the Pulley Speed Ratio Formula,
D1 × N1 = D2 × N2
where, D1 is the diameter of the driving pulley and D2 the diameter of the driven pulley. The pulleys’ rotational speeds are represented by N1 and N2.
This equation works when it operates under the assumption that friction between the belt and pulleys is, like Goldilock’s preferred bed, “just so.” Meaning, friction present is high enough so the belt doesn’t slip, yet loose enough so as not to bring the performance of a rotating piece of machinery to a grinding halt.
Ideally, you want no slippage between belt and pulleys, but the only way for that to happen is if you have perfect friction between their surfaces—something that will never happen because there’s always some degree of slippage. So how do we design a pulley-belt system to maximize friction and minimize slip?
Before we get into that, we must first gain an understanding of how friction comes into play between belts and pulleys. To do so we’ll use the famous Euler-Eytelwein Formula, shown here,
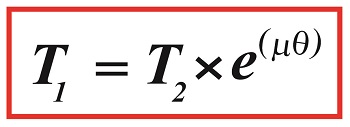
A First Look at the Euler-Eytelwein Formula
where, T1 and T2 are belt tensions on either side of a pulley.
We’ll continue our exploration of the Euler-Eytelwein Formula next time when we discuss the significance of its two sources of tension.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, belt slippage, belt tension, drive belt, engineering, Euler-Eytelwein Formula, friction, mechanical power transmission, pulley, pulley belt system
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on A First Look at the Euler-Eytelwein Formula
Friday, April 21st, 2017
|
Last time we saw how pulley diameter governs speed in engineering scenarios which make use of a belt and pulley system. Today we’ll see how this phenomenon is defined mathematically through application of the Pulley Speed Ratio Formula, which enables precise pulley diameters to be calculated to achieve specific rotational speeds. Today we’ll apply this Formula to a scenario involving a building’s ventilating system.
The Pulley Speed Ratio Formula is,
D1 × N1 = D2 × N2 (1)
where, D1 is the diameter of the driving pulley and D2 the diameter of the driven pulley.
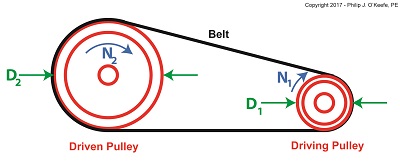
A Pulley Speed Ratio Formula Application
The pulleys’ rotational speeds are represented by N1 and N2, and are measured in revolutions per minute (RPM).
Now, let’s apply Equation (1) to an example in which a blower must deliver a specific air flow to a building’s ventilating system. This is accomplished by manipulating the ratios between the driven pulley’s diameter, D2, with respect to the driving pulley’s diameter, D1. If you’ll recall from our discussion last time, when both the driving and driven pulleys have the same diameter, the entire assembly moves at the same speed, and this would be bad for our scenario.
An electric motor and blower impeller moving at the same speed is problematic because electric motors are designed to spin at much faster speeds than typical blower impellers in order to produce desired air flow. If their pulleys’ diameters were the same size, it would result in an improperly working ventilating system in which air passes through the furnace heat exchanger and air conditioner cooling coils far too quickly to do an efficient job of heating or cooling.
To bear this out, let’s suppose we have an electric motor turning at a fixed speed of 3600 RPM and a belt-driven blower with an impeller that must turn at 1500 RPM to deliver the required air flow according to the blower manufacturer’s data sheet. The motor shaft is fitted with a pulley 3 inches in diameter. What pulley diameter do we need for the blower to turn at the manufacturer’s required 1500 RPM?
In this example known variables are D1 = 3 inches, N1 = 3600 RPM, and N2 = 1500 RPM. The diameter D2 is unknown. Inserting the known values into equation (1), we can solve for D2,
(3 inches) × (3600 RPM) = D2 × (1500 RPM) (2)
Simplified, this becomes,
D2 = 7.2 inches (3)
Next time we’ll see how friction affects our scenario.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, blower, blower impeller, cooling coils, drive belt, driven pulley, driving pulley, electric motor, engineering, heat exchanger, mechanical power transmission, pulley, pulley speed, Pulley Speed Ratio Formula, RPM, ventilating system
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on A Pulley Speed Ratio Formula Application
Friday, March 31st, 2017
|
Last time we introduced two historical legends in the field of engineering who pioneered the science of mechanical power transmission using belts and pulleys, Leonhard Euler and Johann Albert Eytelwein. Today we’ll build a foundation for understanding their famous Euler-Eytelwein Formula through our example of a simple mechanical power transmission system consisting of two pulleys and a belt, and in so doing demonstrate the difference between driven and driving pulleys.
Our example of a basic mechanical power transmission system consists of two pulleys connected by a drive belt. The driving pulley is attached to a source of mechanical power, for example, the shaft of an electric motor. The driven pulley, which is attached to the shaft of a piece of rotating machinery, receives the mechanical power from the electric motor so the machinery can perform its function.
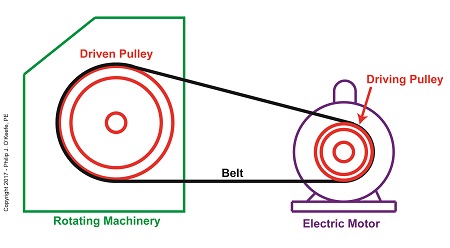
The Difference Between Driven and Driving Pulleys
Next time we’ll see how driven pulleys can be made to spin at different speeds from the driving pulley, enabling different modes of operation in mechanical devices.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, driven pulley, driving pulley, electric motor, engineering, Euler, Euler-Eytelwein Formula, Eytelwein, mechanical power, mechanical power transmission, pulley, pulley speed, rotating machinery
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Difference Between Driven and Driving Pulleys
Monday, March 20th, 2017
|
They say necessity is the mother of invention, and today’s look at an influential historical figure in engineering bears that out. Last week we introduced Leonhard Euler and touched on his influence to the science of pulleys. Today we’ll introduce his contemporary and partner in science, Johann Albert Eytelwein, a German mathematician and visionary, a true engineering trailblazer whose contributions to the blossoming discipline of engineering led to later studies with pulleys.

Johann Albert Eytelwein, Engineering Trailblazer
Johann Albert Eytelwein’s experience as a civil engineer in charge of the dikes of former Prussia led him to develop a series of practical mathematical problems that would enable his subordinates to operate more effectively within their government positions. He was a trailblazer in the field of applied mechanics and their application to physical structures, such as the dikes he oversaw, and later to machinery. He was instrumental in the founding of Germany’s first university level engineering school in 1799, the Berlin Bauakademie, and served as director there while lecturing on many developing engineering disciplines of the time, including machine design and hydraulics. He went on to publish in 1801 one of the most influential engineering books of his time, entitled Handbuch der Mechanik (Handbook of the Mechanic), a seminal work which combined what had previously been mere engineering theory into a means of practical application.
Later, in 1808, Eytelwein expanded upon this work with his Handbuch der Statik fester Koerper (Handbook of Statics of Fixed Bodies), which expanded upon the work of Euler. In it he discusses friction and the use of pulleys in mechanical design. It’s within this book that the famous Euler-Eytelwein Formula first appears, a formula Eytelwein derived in conjunction with Euler. The formula delves into the usage of belts with pulleys and examines the tension interplay between them.
More on this fundamental foundation to the discipline of engineering next time, with a specific focus on pulleys.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: bel, engineering, friction, Johann Albert Eytelwein, mechanical power transmission, pulley, pulleys
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Personal Injury, Product Liability | Comments Off on Johann Albert Eytelwein, Engineering Trailblazer
Tuesday, February 28th, 2017
|
For some time now we’ve been analyzing the helpfulness of the engineering phenomena known as pulleys and we’ve learned that, yes, they can be very helpful, although they do have their limitations. One of those ever-present limitations is due to the inevitable presence of friction between moving parts. Like an unsummoned gremlin, friction will be standing by in any mechanical situation to put the wrench in the works. Today we’ll calculate just how much friction is present within the example compound pulley we’ve been working with.

So How Much Friction is Present in our Compound Pulley?
Last time we began our numerical demonstration of the inequality between a compound pulley’s work input, WI, and work output, WO, an inequality that’s due to friction in its wheels. We began things by examining a friction-free scenario and discovered that to lift an urn with a weight, W, of 40 pounds a distance, d1, of 2 feet above the ground, Mr. Toga exerts a personal effort/force, F, of 10 pounds to extract a length of rope, d2, of 8 feet.
In reality our compound pulley must contend with the effects of friction, so we know it will take more than 10 pounds of force to lift the urn, a resistance which we’ll notate FF. To determine this value we’ll attach a spring scale to Mr. Toga’s end of the rope and measure his actual lifting force, FActual, represented by the formula,
FActual = F + FF (1)
We find that FActual equals 12 pounds. Thus our equation becomes,
12 Lbs = 10 Lbs + FF (2)
which simplifies to,
2 Lbs = FF (3)
Now that we’ve determined values for all operating variables, we can solve for work input and then contrast our finding with work output,
WI = (F × d2) + (FF × d2) (4)
WI = (10 Lbs × 8 feet) + (2 Lbs × 8 feet) (5)
WI = 96 Ft-Lbs (6)
We previously calculated work output, WO to be 80 Ft-Lbs, so we’re now in a position to calculate the difference between work input and work output to be,
WI – WO = 16 Ft-Lbs (7)
It’s evident that the amount of work Mr. Toga puts into lifting his urn requires 16 more Foot-Pounds of work input effort than the amount of work output produced. This extra effort that’s required to overcome the pulley’s friction is the same as the work required to carry a weight of one pound a distance of 16 feet. We can thus conclude that work input does not equal work output in a compound pulley.
Next time we’ll take a look at a different use for pulleys beyond that of just lifting objects.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: compound pulley, engineering, friction, pulley, work, work input, work output
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on So How Much Friction is Present in our Compound Pulley?
Monday, January 16th, 2017
|
We left off last time with an engineering analysis of energy factors within a compound pulley scenario, in our case a Grecian man lifting an urn. We devised an equation to quantify the amount of work effort he exerts in the process. That equation contains two terms, one of which is beneficial to our lifting scenario, the other of which is not. Today we’ll explore these two terms and in so doing show how there are situations when work input does not equal work output.
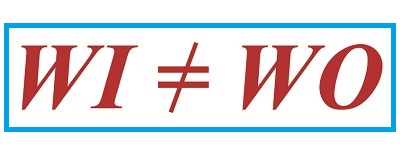
Work Input Does Not Equal Work Output
Here again is the equation we’ll be working with today,
WI = (F × d) + (FF × d) (1)
where, F is the entirely positive force, or work, exerted by human or machine to lift an object using a compound pulley. It represents an ideal but not real world scenario in which no friction is present within the pulley assembly.
The other force at play in our lifting scenario, FF, is less obvious to the casual observer. It’s the force, or work, which must be employed over and above the initial positive force to overcome the friction that’s always present between moving parts, in this case a rope moving through pulley wheels. The rope length extracted from the pulley to lift the object is d.
Now we’ll use this equation to understand why work input, WI, does not equal work output, WO, in a compound pulley arrangement where friction is present.
The first term in equation (1), (F × d), represents the work input as supplied by human or machine to lift the object. It is an idealistic scenario in which 100% of energy employed is directly conveyed to lifting. Stated another way, (F × d) is entirely converted into beneficial work effort, WO.
The second term, (FF × d), is the additional work input that’s needed to overcome frictional resistance present in the interaction between rope and pulley wheels. It represents lost work effort and makes no contribution to lifting the urn off the ground against the pull of gravity. It represents the heat energy that’s created by the movement of rope through the pulley wheels, heat which is entirely lost to the environment and contributes nothing to work output. Mathematically, this relationship between WO, WI, and friction is represented by,
WO = WI – (FF × d) (2)
In other words, work input is not equal to work output in a real world situation in which pulley wheels present a source of friction.
Next time we’ll run some numbers to demonstrate the inequality between WI and WO.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: compound pulley, engineering, friction, heat energy, pulley, work input, work output
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Work Input Does Not Equal Work Output
Saturday, January 7th, 2017
|
Last time we saw how the presence of friction reduces mechanical advantage in an engineering scenario utilizing a compound pulley. We also learned that the actual amount of effort, or force, required to lift an object is a combination of the portion of the force which is hampered by friction and an idealized scenario which is friction-free. Today we’ll begin our exploration into how friction results in reduced work input, manifested as heat energy lost to the environment. The net result is that work input does not equal work output and some of Mr. Toga’s labor is unproductive.
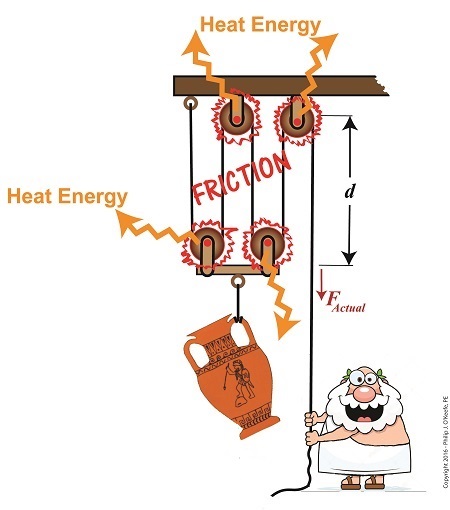
Friction Results in Heat and Lost Work Within a Compound Pulley
In a past blog, we showed how the actual force required to lift our urn is a combination of F, an ideal friction-free work effort by Mr. Toga, and FF , the extra force he must exert to overcome friction present in the wheels,
FActual = F + FF (1)
Mr. Toga is clearly working to lift his turn, and generally speaking his work effort, WI, is defined as the force he employs multiplied by the length, d, of rope that he pulls out of the compound pulley during lifting. Mathematically that is,
WI = FActual × d (2)
To see what happens when friction enters the picture, we’ll first substitute equation (1) into equation (2) to get WI in terms of F and FF,
WI = (F + FF ) × d (3)
Multiplying through by d, equation (3) becomes,
WI = (F × d )+ (FF × d) (4)
In equation (4) WI is divided into two terms. Next time we’ll see how one of these terms is beneficial to our lifting scenario, while the other is not.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: compound pulley, engineering, friction, heat energy, lost work, mechanical advantage, pulley, reduced work, work input, work output
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Friction Results in Heat and Lost Work Within a Compound Pulley
Tuesday, December 13th, 2016
|
The presence of friction in mechanical designs is as guaranteed as conflict in a good movie, and engineers inevitably must deal with the conflicts friction produces within their mechanical designs. But unlike a good movie, where conflict presents a positive, engaging force, friction’s presence in pulleys results only in impediment, wasting energy and reducing mechanical advantage. We’ll investigate the math behind this phenomenon in today’s blog.
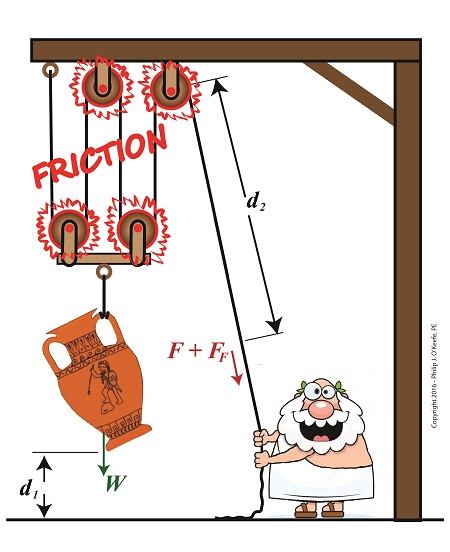
Friction Reduces Pulleys’ Mechanical Advantage
A few blogs back we performed a work input-output analysis of an idealized situation in which no friction is present in a compound pulley. The analysis yielded this equation for mechanical advantage,
MA = d2 ÷ d1 (1)
where d2 is the is the length of rope Mr. Toga extracts from the pulley in order to lift his urn a distance d1 above the ground. Engineers refer to this idealized frictionless scenario as an ideal mechanical advantage, IMA, so equation (1) becomes,
IMA = d2 ÷ d1 (2)
We also learned that in the idealized situation mechanical advantage is the ratio of the urn’s weight force, W, to the force exerted by Mr. Toga, F, as shown in the following equation. See our past blog for a refresher on how this ratio is developed.
IMA = W ÷ F (3)
In reality, friction exists between a pulley’s moving parts, namely, its wheels and the rope threaded through them. In fact, the more pulleys we add, the more friction increases.
The actual amount of lifting force required to lift an object is a combination of FF , the friction-filled force, and F, the idealized friction-free force. The result is FActual as shown here,
FActual = F + FF (4)
The real world scenario in which friction is present is known within the engineering profession as actual mechanical advantage, AMA, which is equal to,
AMA = W ÷ FActual (5)
To see how AMA is affected by friction force FF, let’s substitute equation (4) into equation (5),
AMA = W ÷ (F + FF) (6)
With the presence of FF in equation (6), W gets divided by the sum of F and FF . This results in a smaller number than IMA, which was computed in equation (3). In other words, friction reduces the actual mechanical advantage of the compound pulley.
Next time we’ll see how the presence of FF translates into lost work effort in the compound pulley, thus creating an inequality between the work input, WI and work output WO.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: actual mechanical advantage, AMA, compound pulley, engineering, friction, friction force, ideal mechanical advantage, IMA, mechanical advantage, mechanical design, pulley, pulley friction, pulley work input, pulley work output, weight force
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Friction Reduces Pulleys’ Mechanical Advantage