|
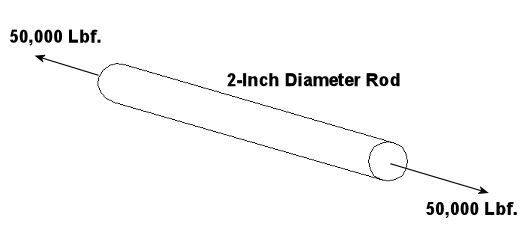
When we looked at our statics example a few posts ago, it was convenient to consider the bridge beam as being perfectly rigid. In the real world, a bridge beam is not perfectly rigid. When it’s subjected to external forces, like the weight of a truck sitting in the middle of it, there is a tendency for it to bend, deform, change its shape. If the external forces create bending and deformations that are too much for the bridge beam material to handle, it will collapse. In strengths of materials analysis, engineers must consider typical stresses that will occur within objects like bridge beams, airplane wings, bolts, and machine parts during use. Stress is a measure of force exerted per unit area of a surface. Once the stresses are known, a material is selected that is strong enough to keep the object from being bent, mashed, stretched, and/or broken. To illustrate this, let’s consider an example of a simple stress. Suppose you want to design a truss rod for a highway bridge like the one shown in Figure 1. Specifications require that the rod be two inches in diameter. Its purpose is to hold the sides of the bridge together when vehicles travel across it. Figure 1 Now suppose that the bridge is to handle traffic to and from and iron mine. Let’s consider the scenario where a truck laden with iron ore runs out of gas and comes to a stop in the middle of our bridge. Under this load, static analysis reveals that the sides of the bridge want to spread apart, putting a tension of 50,000 pounds force (Lbf.) on the truss rod as shown in Figure 2. Figure 2 Since the external force acting upon the truss rod and the diameter of the rod itself are both given, the engineer would merely have to select the appropriate material for the rod that would fall within the desired parameters, that is, so as to keep our rod from pulling apart when anticipated stressors such as a heavy truck is on the bridge. The first step would be to calculate the tensile stress within the rod itself. By tensile stress, I mean the stress in the rod due to the forces that are trying to pull it apart. In our example, this is relatively easy to assess: Stress = [Tensile Force] ÷ [Lateral Cross Sectional Area of the Rod] The lateral cross section of the rod is round, so its area would be πd2 divided by 4, where the Greek letter π (Pi) has a value of 3.1416, and d is the diameter of the rod. Therefore, the tensile stress would be: Stress = [50,000 Lbf.] ÷ [π × (2 in.)2 ÷ 4] = 15,915.49 Lbf./in.2 Knowing the stress within the rod, the engineer would next have to select an appropriate material for the rod that’s strong enough to do the job. In our case, let’s say we determine that steel is the best material to use. But what type of steel? Well, there are engineering handbooks with tables that list the mechanical properties of all sorts of materials, including metals and plastics, and along with those properties there is listed their ability to handle stress. These mechanical properties were determined in laboratory tests where carefully machined specimens of the materials were subjected to measured stresses until they deformed and broke apart. They include yield strength and ultimate strength, and these findings have been duly recorded so that future engineers need not go through independent testing of common materials themselves. Yield strength is the stress that is measured when the test specimen begins to stretch without any significant increase in force being applied to it. Ultimate strength is the maximum stress that the material in the test specimen can withstand before it starts to fail, that is tear apart, break, collapse. Our engineer would use the mechanical properties tables that are readily available to him to select the appropriate steel alloy that would meet our criteria, that is, has a listed strength high enough above the calculated 15,915.49 Lbf./in.2 tensile stress to provide a sufficient factor of safety. Factors of safety are listed in engineering books for yield strength and ultimate strength and they are selected depending on how the forces are applied to a structural component or machine part (e.g. steady, varying, or shock). When strengths of materials analysis involves the solution of complex statics and dynamics problems, things become a little less straightforward. And when you are dealing with components having odd shapes and a combination of stresses, say due to compression and torsion, things become even more complex. In any case, engineers must have extensive knowledge of the properties of materials in order to anticipate factors at play in real world scenarios such as the one we’ve been discussing. Ever wonder why some steel is hard and brittle, and some is soft and bendable? Well, our next topic of discussion will be about materials science, the study of how metal alloys and polymers are formed to have specific properties. _________________________________________________________________ |
Posts Tagged ‘statics’
Strengths of Materials in Mechanical Engineering
Sunday, November 15th, 2009Mechanical Engineering, Focus on Statics
Sunday, October 18th, 2009|
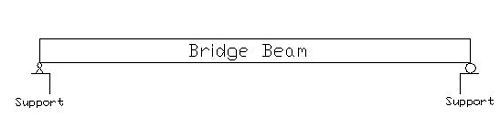
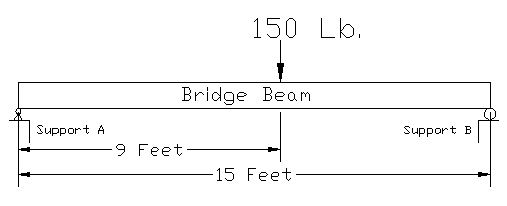
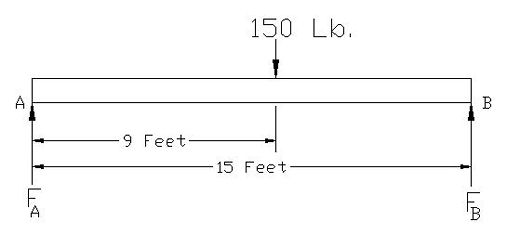
As I stated in my last blog post, Statics is the study of how forces are transmitted to and throughout stationary objects. Let’s learn a little bit about how statics is used by mechanical engineers to solve problems. Consider a perfectly rigid bridge beam sitting on two supports (see Figure 1). Now suppose you decide to stand on it. The weight of your body would push down on the beam, creating a system of forces that act upon the beam. If the beam stays on its supports and doesn’t move (it remains static), then the forces are said to be in “equilibrium.” In other words, since the beam doesn’t move when you stand on it, the sum of all the forces acting upon it are zero. Figure 1 So what, you say? Well, this concept of forces in equilibrium helps mechanical engineers analyze external and internal forces acting on stationary objects that have importance to us in real life, like bridges, machines, traffic signal masts, etc. This analysis is used to calculate the magnitudes of all the forces acting on these objects so they can design parts of the objects to be strong enough not to break apart. Think about that next time you get ready to cross a bridge in your car. To show how this works, consider the bridge beam scenario I discussed above. Suppose you weigh 150 pounds and you stand nine feet from the left end of the bridge beam (see Figure 2). Your weight will exert a downward force of 150 pounds upon the beam (let’s ignore the weight of the beam in this case). The weight of your body creates reaction forces on the beam at Support A and Support B. To consider these reaction forces, the mechanical engineer would draw what is called a “free body diagram” (see Figure 3). Figure 2 Figure 3 The reaction forces (FA and FB) at the supports A and B push up on the bottom of the beam. If the beam remains static, then the sum of the reaction forces will equal the 150 pound weight force from your body. That is, the reaction forces cancel out the 150 pound force if the beam doesn’t move and they are said to be in equilibrium. But in our example above, you’re not standing in the exact center of the beam, hence the two reaction forces are not going to be equal. More of your body weight force is bearing down on Support B and less on Support A. So how do you determine the values of the reaction forces in a situation like this? You consider “moments.” A moment is mechanical engineering lingo for a force multiplied by a distance. Moments want to rotate objects. This is an important concept in statics because if an object doesn’t move, it certainly won’t rotate, so the sum of all the moments acting on the object are zero. So, in the case of our bridge beam, the sum of the moments acting on Support A would be zero, or mathematically speaking: Sum MA = [(FA) x (0 Feet)] – [(150 Lb.) x (9 Feet)] + [(FB) x (15 Feet)] = 0 Using algebra, you can find the value for the reaction force at Support B: [0] – [(150 Lb.) x (9 Feet)] + [(FB) x (15 Feet)] = 0 [(FB) x (15 Feet)] = [(150 Lb.) x (9 Feet)] FB = 90 Lb. So what about the reaction force at Support A? If you remember, I said that if the bridge beam remains static, then the sum of all the forces acting on it will be zero. Knowing that, you can use algebra to solve for the reaction force at Support A: FA -150 Lb + FB = 0
FA = 150 Lb. – 90 Lb. = 60 Lb. So that is the basic concept of statics. Remember, in statics, nothing moves, so mechanical engineers use that to their advantage when they analyze forces acting on objects. Our next topic will be: Dynamics, the study of the effects of velocity and acceleration and resulting forces and the energy of moving objects. Last week’s Riddle: Everyone knows us to be racing by when they look at a clock, but mechanical engineers also know us to add up to zero when they look at a fixed structure. What are we? Answer: Moments _________________________________________________________________ |