|
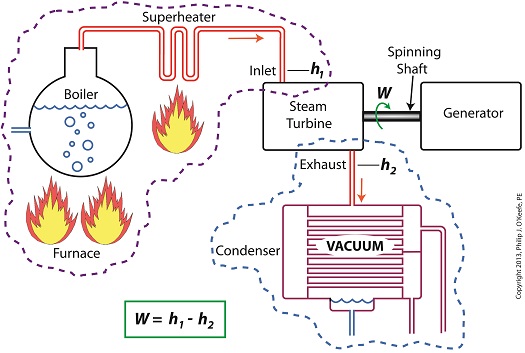
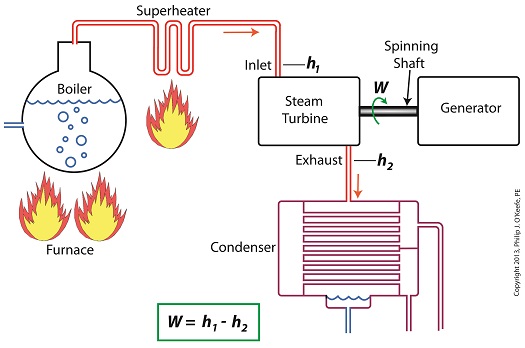
Last time we ran our basic power plant steam turbine without a condenser. In that configuration the steam from the turbine exhaust was simply discharged to the surrounding atmosphere. Today we’ll connect it to a condenser to see how it improves the turbine’s efficiency. As discussed in a previous blog, enthalpy h1 is solely dependent on the pressure and temperature at the turbine inlet. For purposes of today’s discussion, turbine inlet steam pressure and temperature will remain as last time, with values of 2,000 lbs PSI and 1000°F respectively, and calculations today will be based upon those values. So to review, the inlet enthalpy h1 is, h1 = 1474 BTU/lb If the condenser vacuum exists at a pressure of 0.6 PSI, a realistic value for a power plant condenser, then referring to the steam tables in the Van Wylen and Sonntag thermodynamics book, we find that the enthalpy h2 will be, h2 = 847 BTU/lb and the amount of useful work that the turbine can perform with the condenser in place would therefore be, W = h1 – h2 = 1474 BTU/lb – 847 BTU/lb = 627 BTU/lb So essentially with the condenser present, the work of the turbine is increased by 168 BTU/lb (627 BTU/lb – 459 BTU/lb). To put this increase into terms we can relate to, consider this. Suppose there’s one million pounds of steam flowing through the turbine each hour. Knowing this, the turbine power increase, P, is calculated to be, P = (168 BTU/lb) ´ (1,000,000 lb/hr) = 168,000,000 BTU/hr Now according to Marks’ Standard Handbook for Mechanical Engineers, a popular general reference book in mechanical engineering circles, one BTU per hour is equivalent to 0.000393 horsepower, or HP. So converting turbine power, P, to horsepower, HP, we get, P = (168,000,000 BTU/hr) ´ (0.000393 HP/BTU/hr) = 66,025 HP A typical automobile has a 120 HP engine, so this equation tells us that the turbine horsepower output was increased a great deal simply by adding a condenser to the turbine exhaust. In fact, it was increased to the tune of the power behind approximately 550 cars! What all this means is that the stronger the vacuum within the condenser, the greater the difference between h1 and h2 will be. This results in increased turbine efficiency and work output, as evidenced by the greater numeric value for W. Put another way, the turbine’s increased efficiency is a direct result of the condenser’s vacuum forming action and its recapturing of the steam that would otherwise escape from the turbine’s exhaust into the atmosphere. This wraps up our series on the power plant water-to-steam cycle. Next time we’ll use the power of 3D animation to turn a static 2D image of a centrifugal clutch into a moving portrayal to see how it works. ________________________________________ |
Posts Tagged ‘steam pressure’
How Condensers Increase Efficiency Inside Power Plants
Wednesday, December 4th, 2013Enthalpy and the Potential for More Work
Monday, November 18th, 2013|
Last time we learned how enthalpy is used to measure heat energy contained in the steam inside a power plant. The higher the steam pressure, the higher the enthalpy, and vice versa, and we touched upon the concept of work, or the potential for a useful outcome of a process. Today we’ll see how to get the maximum work out of a steam turbine by attaching a condenser at the point of its exhaust and making the most of the vacuum that exists within its condenser. Let’s revisit the equation introduced last time, which allows us to determine the amount of useful work output: W = h1 – h2 Applied to a power plant’s water-to-steam cycle, enthalpy h1 is solely dependent on the pressure and temperature of steam entering the turbine from the boiler and superheater, as contained within the purple dashed line in the diagram below. As for enthalpy h2, it’s solely dependent on the pressure and temperature of steam within the condenser portion of the water-to-steam cycle, as shown by the blue dashed circle of the diagram. Next week we’ll see how the condenser, and more specifically the vacuum inside of it, sets the platform for increased energy production, a/k/a work.
________________________________________ |
Enthalpy and Steam Turbines
Thursday, November 14th, 2013|
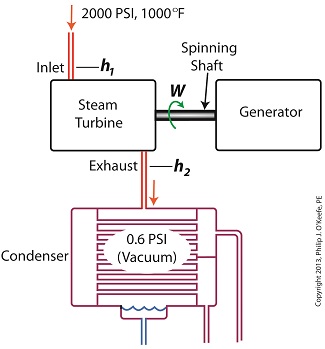
Last time we learned how the formation of condensate within a power plant’s turbine results in a vacuum being created. This vacuum plays a key role in increasing steam turbine efficiency because it affects a property known as enthalpy, a term used to denote total heat energy contained within a substance. For the purposes of our discussion, that would be the heat energy contained within steam which flows through the turbine in a power plant. The term enthalpy was first introduced by scientists within the context of the science of thermodynamics sometime in the early 20th Century. As discussed in a previous blog article, thermodynamics is the science that deals with heat and work present within processes. Enthalpy is a key factor in thermodynamics, and is commonly represented in engineering calculations by the letter h and denoted as, h = u + Pv where u is the internal energy of a substance, let’s say steam; P is the pressure acting upon a specific volume, v, of the steam; and P and v are multiplied together. Pressure is force per unit area and is measured in psi, pounds per square inch. For the purposes of our discussion, it’s the amount of pressure that steam places on pipes containing it. Looking at the equation above, simple math tells us that if we increase the pressure, P, the result will be an increase in enthalpy h. If we decrease P, the result will be a decrease in h. Now, let’s see why this property is important with regard to the operation of a steam turbine. When it comes to steam turbines, thermodynamics tells us that the amount of work they perform is proportional to the difference between the enthalpy of the steam entering the turbine and the enthalpy of the steam at the turbine’s exhaust. What is meant by work is the act of driving the electrical generator, which in turn provides electric power. In other words, the work leads to a useful outcome. This relationship is represented by the following equation, W = h1 – h2 In terms of the illustration below, W stands for work, or potential for useful outcome of the turbine/generator process in the form of electricity, h1 is the enthalpy of the steam entering the inlet of the turbine from the superheater, and h2 is the enthalpy of the steam leaving at the turbine exhaust. We’ll discuss the importance of enthalpy in more detail next week, when we’ll apply the concept to the work output of a steam turbine.
________________________________________ |