Posts Tagged ‘velocity’
Monday, January 11th, 2016
|
Last time my engineering expertise was put to the test when it was discovered that Santa’s sleigh was being hampered by a strong gust of wind. At that time we introduced the Work-Energy Theorem to determine how strong the wind’s opposing force was, and today we’ll work with the Theorem to compute just what Rudolph was up against. Here again is the expanded, workable version of the Work-Energy Theorem as introduced last time,
F × d = ½ × m × [v22 – v12]
where F is a force acting upon a moving object of mass m over a distance d to slow it from an initial velocity of v1 to a final velocity of v2.
Applying the Theorem to the dynamics at play in Santa’s situation, F is the opposing wind force, which acts over a distance, d, to slow his sleigh from an initial velocity of v1 to a final velocity, v2, thus presenting Rudolph and his buddies with a real delivery challenge.
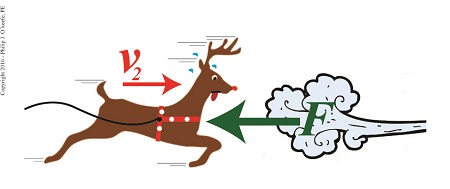 Rudolph Struggles Against a Fierce Wind Rudolph Struggles Against a Fierce Wind
If we know that Santa, his sleigh and reindeer have a combined mass of 900 kilograms — which is pretty standard for a fully loaded sleigh and reindeer team — and their initial velocity was 90 meters per second, final velocity 40 meters per second, and the distance over which the slowing took place was 760 meters, then the formula to calculate the opposing wind force becomes,
F × d = ½ × m × [v22 – v12]
F = ½ × m × [v22 – v12] ÷ d
F = ½ × (900kg) × [(40 meters/sec)2 – (90 meters/sec)2] ÷ 760 meters
F = -3848.7 Newtons = -865.2 Pounds
The minus sign signifies that the wind must exert an opposing force of 865.2 pounds in order to slow Santa’s sleigh down.
In order for Santa to get back on his delivery schedule, Rudolph is going to have to make up for lost time by expending extra energy. We’ll see how he does that next time.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, engineering expert, force, mass, Newtons, pounds, velocity, Work-EnergyTheorem
Posted in Engineering and Science, Expert Witness, Innovation and Intellectual Property, Personal Injury | Comments Off on The Work-Energy Theorem Applied to Santa’s Sleigh
Friday, January 1st, 2016
|
As an engineering expert I’ve applied the Work-Energy Theorem to diverse situations, but none as unique as its most recent application, the progress of Santa’s sleigh. Last week we saw how Santa and his reindeer team encountered a wind gust which generated enough force to slow them from an initial velocity of v1 to a final velocity, v2, over a distance, d. Today we’ll begin using the Work-Energy Theorem to see if Santa was able to keep to his Christmas delivery schedule and get all the good boys and girls their gifts in time.

Before we can work with the Work-Energy Theorem, we must first revisit the formula it’s predicated upon, de Coriolis’ formula for kinetic energy,
KE = ½ × m × v2 (1)
where, KE is kinetic energy, m is the moving object’s mass, and v its velocity.
The equation behind the Work-Energy Theorem is,
W = KE2 – KE1 (2)
where W is the work performed, KE1 is the moving object’s initial kinetic energy and KE2 its final kinetic energy after it has slowed or stopped. In cases where the object has come to a complete stop KE2 is equal to zero, since the velocity of a stationary object is zero.
In order to work with equation (2) we must first expand it into a more useful format that quantifies an object’s mass and initial and final velocities. We’ll do that by substituting equation (1) into equation (2). The result of that term substitution is,
W = [½ × m × v22 ] – [½ × m × v12] (3)
Factoring out like terms, equation (3) is simplified to,
W = ½ × m × [v22 – v12] (4)
Now according to de Coriolis, work is equal to force, F, times distance, d. So substituting these terms for W in equation (4), the expanded version of the Work-Energy Theorem becomes,
F × d = ½ × m × [v22 – v12] (5)
Next time we’ll apply equation (5) to Santa’s delivery flight to calculate the strength of that gust of wind slowing him down.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis, distance, energy, engineering expert, force, kinetic energy, mass, velocity, wind force, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury | Comments Off on The Math Behind the Work-Energy Theorem
Friday, December 25th, 2015
|
I hope all the good little boys and girls got Santa’s presents, because his sleigh was spotted yesterday on radar moving at an alarmingly slow pace.
As the radar screen here shows, the progress of Santa and his reindeer had slowed from an initial velocity of v1 to a much slower velocity of v2 over the distance, d, he traveled from his workshop.
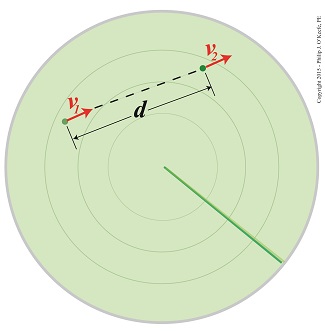
Santa’s Sleigh Tracked On Radar
Upon closer examination, the radar operator noted that the North Wind was especially powerful this year, which caused Rudolph and the gang to double their efforts to overcome its negative force.

Santa and His Reindeer Fighting The Wind
Did Santa make it in time to deliver Christmas presents? Find out next time, when we put the developing drama into the form of mathematical equations.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, force, velocity, work-energy theorem
Posted in Engineering and Science | Comments Off on The Work-Energy Theorem Affects Santa’s Sleigh!
Monday, September 28th, 2015
|
Last time we introduced Gaspard-Gustave de Coriolis’ formula to compute kinetic energy. Today we’ll use it to determine the speed of descent, or velocity, of the coffee mug we’ve been watching closely in the last few blogs. To calculate the mug’s velocity, we must bear in mind physicist Julius Robert von Mayer’s assertion that all forms of energy are interrelated, and in fact interchangeable, because energy can neither be created nor destroyed, it can only change forms. For a refresher, see The Law of Conservation of Energy.
Let’s now put a practical spin on this concept and apply it to our coffee mug’s free fall to the floor. Once again, de Coriolis’ formula,
KE = ½ × m × v2 (1)
where m is the mass of our falling object and v its velocity. The ½ is an unchanging, constant term that’s present due to the mathematical Rules of Integration governing integral calculus. Calculus and its derivations are beyond the scope of this blog, but if you’re interested in pursuing this, follow this link to, The Physics Hypertextbook – Kinetic Energy.
According to von Mayer’s Law, at the precise instant before the mug hits the floor its kinetic energy, KE, is equal to the potential energy, PE, it possessed when it rested passively on the shelf. Stated another way, the instant before the mug makes contact with the floor, all its potential energy will have been converted into kinetic.
The mug’s PE was calculated previously to be equal to 4.9 kg • meter2/second2. See Computing Potential Energy for a review. Knowing this, the mathematical relationship between the mug’s potential and kinetic energies is expressed as,
PE = KE = 4.9 kg • meter2/second2 (2)
By substituting this mathematical representation for KE into equation (1) we arrive at,
4.9 kg • meter2/second2 = ½ × m × v2 (3)
We also know the mug’s mass, m, to be equal to 2.6 kilograms, so integrating that into the right side of equation (3) it becomes,
4.9 kg • meter2/second2 = ½ × ( 0.25kg) × v2 (4)
That leaves the mug’s velocity, v2, as the only remaining unknown term. We’ll use algebra to isolate this variable by dividing both sides of equation (4) by ½ × ( 0.25kg).
(4.9 kg • meter2/second2) ÷ [½ × ( 0.25kg)] = v2
39.20 meter2/second2 = v2
Finally, we’ll take the square root of the equation to place it in terms of v.
6.26 meters/second = v
The mug’s velocity an instant before impact equates to 6.26 meters/second, or almost 21 feet per second.
Next time we’ll discuss a metric unit used to measure energy known as the Joule and discover the man behind it.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: energy conversion, falling velocity, forensic engineering de Coriolis, integral calculus, joule, Julius Robert von Mayer, kinetic energy, law of conservation of energy, mechanical engineering expert witness, physics, potential energy, velocity, velocity of falling objects
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Calculating Velocity — de Coriolis’ Kinetic Energy Formula
Friday, September 18th, 2015
|
Last time we introduced kinetic energy as the energy of movement. Today we’ll see how to calculate it, using French mathematician Gaspard-Gustave de Coriolis’ formula as set out in his textbook, Calculation of the Effect of Machines. We’ll then apply his formula to our example of a coffee mug falling from its shelf.
Gaspard-Gustave de Coriolis’ book presented physics concepts, specifically the study of mechanics, in an accessible manner, without a lot of highbrow theory and complicated mathematics. His insights made complicated subjects easy to understand, and they were immediately put to use by engineers of his time, who were busily designing mechanical devices like steam engines during the early stages of the Industrial Revolution.
Within its pages the mathematics of kinetic energy was presented in the scientific form that persists to present day. That formula is,
KE = ½ × m × v2
where m is the moving object’s mass and v its velocity.
In the case of our coffee mug, its kinetic energy will be zero so long as it remains motionless on the shelf. A human arm had lifted it to its perch against the force of gravity, thereby investing it with gravitational potential energy. If the mug was sent freefalling to the ground by the mischievous kitty, its latent potential energy would be realized and converted into the kinetic energy of motion.

To illustrate, let’s say a mug with a mass equal to 0.25 kg rests on a shelf 2 meters above the floor. Its potential energy would then be equal to 4.9 kg • meter2/second2, as was computed in our previous blog, Computing Potential Energy.
Once kitty nudges the mug from its perch and it begins to fall, its latent gravitational potential energy begins a conversion process from potential to kinetic energy. It will continue to convert into an amount of kinetic energy that’s precisely equal to the mug’s potential energy while at rest on the shelf, that is, 4.9 kg • meter2/second2. Upon impact with the floor, all the mug’s gravitational potential energy will have been converted into kinetic energy.
Next time we’ll apply the Law of Conservation of Energy to the potential and kinetic energy formulas to calculate the mug’s velocity as it freefalls to the floor.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: Calculation of the Effect of Machines, engineering expert witness, engines, falling objects, Gaspard-Gustave de Coriolis, kinetic energy, machinery, mass, mechanical energy, mechanical engineer, mechanics, physics, potential energy, velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Calculation of the Effect of Machines — How to Calculate Kinetic Energy
Friday, September 11th, 2015
|
Last time we introduced The Law of Conservation of Energy, which holds that energy can neither be created nor destroyed. We then applied the concept to a mug resting on a shelf, brimming with latent gravitational potential energy. Today we’ll continue our discussion with a focus on kinetic energy and how Willem Gravesande’s experimentation contributed to our understanding of the subject.
The concept of kinetic energy was first posited by mathematicians Gottfried Leibniz and Johann Bernoulli in the early 18th Century when they theorized that the energy of a moving object is a factor of its mass and speed. Their theory was later proven by Willem Gravesande, a Dutch lawyer, philosopher, and scientist.
Gravesande conducted experiments in which he dropped identical brass balls into a soft clay block. See Figure 1.
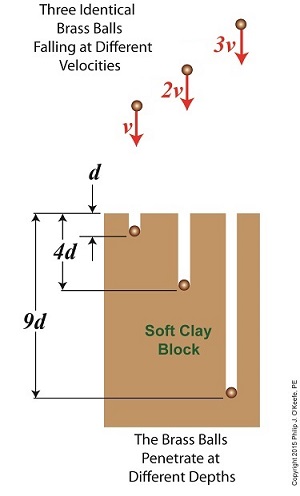
Figure 1
Figure 1 shows the results obtained when balls of the same mass m are dropped from various heights, resulting in different velocities as they fall and different clay penetrations. The ball on the left falls at velocity v and penetrates to a depth d. The center ball falls at twice the left ball’s velocity, or 2v, and penetrates four times as deep, or 4d. The right ball falls at three times the left ball’s velocity, 3v, and it penetrates nine times deeper, 9d. The results indicate an exponential increase in clay penetration, dependent on the balls’ speed of travel.
In fact, all the kinetic energy that the balls exhibited during freefall was converted into mechanical energy from the instant they impacted the clay until their movement within it stopped. This change in forms of energy from kinetic to mechanical demonstrates what Julius Robert von Mayer had in mind when he derived his Law of Conservation of Energy. For a refresher on the subject, see last week’s blog, The Law of Conservation of Energy.
As a result of his experimentation, Gravesande was able to conclude that the kinetic energy of all falling objects is a factor of their mass multiplied by their velocity squared, or m × v2.
We’ll see next time how Gravesande’s work paved the way for later scientists to devise the actual formula used to calculate kinetic energy and then we’ll apply it all to our coffee mug falling from the shelf.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: falling objects, forensic engineer, Gottfried Leibniz, impact, Johann Bernoulli, Julius Robert von Mayer, kinetic energy, mass, mechanical energy, mechanical engineering expert witness, penetration, potential energy, velocity, Willem Gravesande
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Willem Gravesande’s Experimentation on Kinetic Energy
Tuesday, July 28th, 2015
|
Last time we began our discussion on velocity by focusing on one of its aspects, distance, and we calculated Earth’s orbital distance around the sun to be 5,816,023,200 miles. Today we’ll focus on velocity’s other aspect, time. Together, these aspects will allow us to solve for Earth’s orbital velocity, aka speed.
When early astronomers monitored Earth’s journeys, they found it took exactly one year for it to complete its orbit around the sun. They combined this fact with Earth’s orbital travel distance of 5,816,023,200, or 9.36 × 1011 meters — meters being the unit of measurement most often used in scientific computations — and solved for Earth’s orbital velocity as follows,
v = 9.36 × 1011 meters ÷ 1 year = 9.36 × 1011 meters per year
The scientific notation of 9.36 × 1011 equates to 936,000,000,000 meters, a large and unruly number to work with. We can simplify things further by breaking this number down into units of meters per second, which will then allow us to arrive at Earth’s velocity in terms of miles per hour, something most Earthlings can relate to.
One meter per second is equal to 2.237 miles per hour, and there are 31,536,000 seconds in one year, so breaking Earth’s orbital velocity down into meters per second we arrive at,
v = 9.36 × 1011 meters ÷ 31,536,000 seconds = 29,680 meters per second
v = (29,680 meters per second) × (2.237 mph/m/sec) = 66,394 miles per hour
Yes, it’s true, Earth whips around the sun at warp speed. Our fastest man made rockets only achieve speeds of about 25,000 miles per hour. Earth beats them two-to-one!

Now that we know Earth’s orbital velocity, we have everything we need to calculate the gravitational force exerted on Earth by the sun. We’ll do that next time.
____________________________________
|
Tags: Earth's orbital velocity, engineering expert witness, force of gravity, forensic engineer, mechanical engineering expert, speed, velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Earth’s High Speed Race Around the Sun
Sunday, July 19th, 2015
|
Last time we introduced Newton’s equation to calculate the sun’s gravitational force acting upon Earth, and today we’ll begin solving for the last remaining unsolved variable within that equation, v, Earth’s orbital velocity.
Here again is Newton’s equation,
Fg = [m × v2] ÷ r
For a refresher on how we solved for m, Earth’s mass, and r, the distance between Earth and the sun, follow these links to past blogs in this series, What is Earth’s Mass and Calculating the Distance to the Sun.
Velocity, or speed, as it’s most commonly referred to, is based on both time and distance. To bear this out we’ll use an object and situation familiar to all of us, traveling in a car. The car’s velocity is a factor of both the distance traveled and the time it takes to get there. A car traveling at a velocity of 30 miles per hour will cover a distance of 30 miles in one hour’s time. This relationship is borne out by the formula,
vCar = distance traveled ÷ travel time
vCar = 30 miles ÷ 1 hour = 30 miles per hour
Similarly, v is the distance Earth travels during its orbital journey around the sun within a specified period of time. It had been observed since ancient times that it takes Earth one year to complete one orbit, so all that remained to be done was calculate the distance Earth traveled during that time. Vital to calculations was the fact that Earth’s orbit is a circle, which allows geometry to be employed and calculations to be thereby simplified. Refer to Figure l.
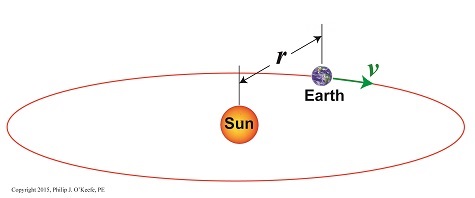
Figure 1
From geometry we know that the circumference of a circle, C, is calculated by,
C = 2× π × r
where π is a constant, the well known mathematical term pi, which is equal to 3.1416, and r is the radius of Earth’s circular orbit, determined, courtesy of the work of Johannes Kepler and Edmund Halley, to be approximately 93,000,000 miles. Stated in metric units, the unit of measurement most often employed in science, that comes to 149,000,000,000 meters.
Inserting these numerical values for π and r into the circumference formula, scientists calculated the distance Earth travels in one orbit around the sun to be,
C = 2 × π × 149,000,000,000 meters = 9.36 x 1011 meters
Next time we’ll introduce the time element into our equations and solve for v, and from there we’ll go on and finally solve for Fg, the sun’s gravitational force acting upon Earth.
____________________________________
|
Tags: astronomical unit, distance traveled, Earth's orbital velocity, Edmund Halley, engineering expert witness, force of gravity, forensic engineer, Isaac Newton, Johannes Kepler, mechanical engineer, radius of Earth's orbit, speed, the AU, travel time, velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Earth’s Orbital Velocity
Thursday, July 9th, 2015
|
Last time we saw how centripetal force is responsible for keeping a child’s ball moving in a circular path when twirled above his head. Today we’ll see how that same force is responsible for keeping Earth in its rotation around the sun. We’ll use Isaac Newton’s Second Law of Motion as it relates to centripetal force to bear that out today.
Our example from last week,
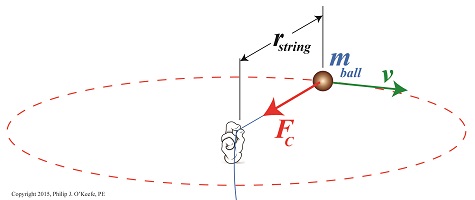
Figure 1
According to Newton’s Second Law of Motion, Fc, the centripetal force acting upon the ball, is calculated by the equation,
Fc = [mball × v2] ÷ rstring
where, mball is the ball’s mass, v the ball’s velocity, and rstring is the length of the string.
The mechanics are obviously different with regard to Earth and its orbit around the sun, where there’s no obvious physical link between the objects in rotation. In this case the sun’s gravitational force, Fg, acts to tether Earth to it. And just like the string and ball, the sun’s gravitational tether creates a centripetal force, Fc, which prevents Earth from leaving its orbital path. See Figure 2.
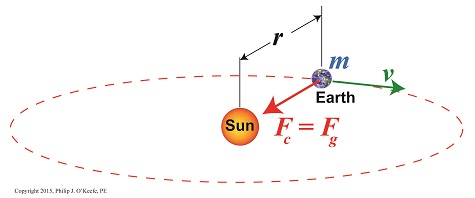
Figure 2
Newton concluded that for the Earth to remain on its permanent, fixed path of orbit around the sun, Fc must be equal to Fg, and that the forces in play between the sun and Earth were like a gigantic tug of war where neither side is able to pull any harder than the other. This stalemate is responsible for keeping Earth stably in place in its orbit.
According to Newton’s Second Law, the sun’s gravitational force acting upon the Earth is calculated by,
Fg = Fc = [m × v2] ÷ r
where, m is Earth’s mass, v its orbital velocity, and r the distance between Earth and the sun. Thanks to early scientists like Edmund Halley and Henry Cavendish, the values for m and r had already been determined. That left v, Earth’s orbital velocity, the only variable remaining to be solved.
We’ll see how 19th Century scientists accomplished that next time.
____________________________________
|
Tags: Cavendish, centripetal force, engineering expert witness, forensic engineer, gravitational force, Halley, Issac Newton's Second Law of Motion, mass, velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Centripetal Force Makes the Earth Go Round
Thursday, September 4th, 2014
|
Picture yourself holding a feather in one hand, a hammer in the other. Your buddy has bet you that if you simultaneously drop them, the hammer will hit the ground first, and he’s got a beer riding on it.
This exact experiment was performed in 1971 by Apollo 15 Astronauts David Scott and Jim Irwin when they landed on the moon. We’ll tell you how it turned out later, but first let’s review the history behind the study of falling objects.
Aristotle, the ancient Greek philosopher, would have bet with your buddy. Back in the 4th Century BC he developed a theory of gravity to explain the physics behind falling objects. He asserted that the heavier the object, the faster it will fall. His theory seems intuitively obvious on its face, but although Aristotle was a great philosopher, he was a lousy scientist. He never ran tests to actually prove his theory. Nevertheless, it was accepted by academics of his time, and it remained the theory of choice until Galileo came along in the 16th Century.
Galileo was a scientist, and he came up with his own theory concerning falling objects. He believed that all falling objects continue to accelerate, picking up speed as they fall, and that this rate of acceleration is the same for all objects, regardless of their weight or density.
The story goes that in 1589, at the age of 25, young Galileo attempted to prove his theory by climbing to the top of the Leaning Tower of Pisa with two balls in hand, one large and heavy, the other small and light. He dropped them at the same time, and guess what happened?

Both balls hit the ground at almost the same time. They would have hit the ground at precisely the same moment had there been no air resistance, a subject which will be discussed at length later in this blog series.
Because Galileo’s experiment was subject to the dense atmosphere of Earth, the influence of air resistance prevented him from proving his theory correct, however he did manage to prove Aristotle’s theory wrong because the balls did not strike the ground at significantly different times.
We’ll see how the astronauts’ experiment turned out next time.
_______________________________________
|
Tags: acceleration, engineering expert witness, falling objects, forensic engineer, mechanical engineering expert, product durability, velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on What Determines Rate of Fall?















