|
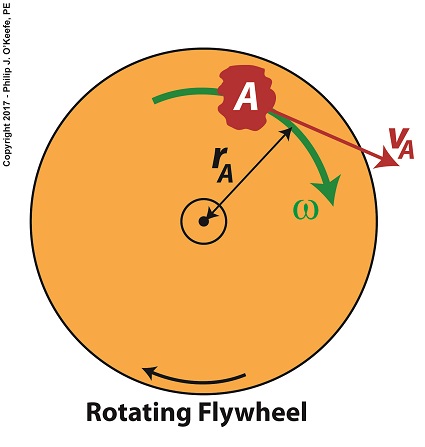
Anyone who has spun a potter’s wheel is appreciative of the smooth motion of the flywheel upon which they form their clay, for without it the bowl they’re forming would display irregularities such as unattractive bumps. The flywheel’s smooth action comes as a result of kinetic energy, the energy of motion, stored within it. We’ll take another step towards examining this phenomenon today when we take our first look at calculating this kinetic energy. To do so we’ll make reference to the two types of velocity associated with a spinning flywheel, angular velocity and linear velocity, both of which engineers must negotiate anytime they deal with rotating objects. Let’s begin by referring back to the formula for calculating kinetic energy, KE. This formula applies to all objects moving in a linear fashion, that is to say, traveling a straight path. Here it is again, KE = ½ × m × v2 where m is the moving object’s mass and v its linear velocity. Flywheels rotate about a fixed point rather than move in a straight line, but determining the amount of kinetic energy stored within a spinning flywheel involves an examination of both its angular velocity and linear velocity. In fact, the amount of kinetic energy stored within it depends on how fast it rotates. For our example we’ll consider a spinning flywheel, which is basically a solid disc. For our illustrative purposes we’ll divide this disc into hypothetical parts, each having a mass m located a distance r from the flywheel’s center of rotation. We’ll select a single part to examine and call that A. Two Types of Velocity Associated With a Spinning Flywheel
Part A has a mass, mA, and is located a distance rA from the flywheel’s center of rotation. As the flywheel spins, part A rides along with it at an angular velocity, ω, following a circular path, shown in green. It also moves at a linear velocity, vA, shown in red. vA represents the linear velocity of part A measured at any point tangent to its circular path. This linear velocity would become evident if part A were to become disengaged from the flywheel and cast into the air, whereupon its trajectory would follow a straight line tangent to its circular path. The linear and angular velocities of part A are related by the formula, vA = rA × ω Next time we’ll use this equation to modify the basic kinetic energy formula so that it’s placed into terms that relate to a flywheel’s angular velocity. This will allow us to define a phenomenon at play in the flywheel’s rotation, known as the moment of inertia.
Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Tags: angular velocity, energy stored, engineering, flywheel, kinetic energy, linear velocity, mass, moment of inertia, spinning flywheel