|
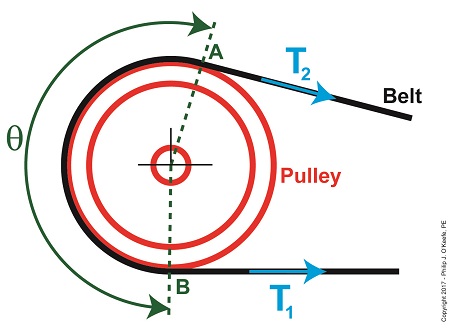
Last time we learned that the two T’s in the Euler-Eytelwein Formula correspond to different belt tensions on either side of a pulley wheel in a pulley-belt assembly. Today we’ll see what the remaining variables in this famous Formula are all about, paying special attention to the angle of wrap that’s formed by the belt wrapping around the pulley wheel. Angle of Wrap in the Euler-Eytelwein Formula Here again is the Euler-Eytelwein Formula, T1 = T2 × e(μθ) The tight side tension, T1, is equal to a combination of factors, namely: loose side tension T2 ; the friction that exists between the belt and pulley, denoted as μ ; and the length of belt coming in direct contact with the pulley, namely, θ. These last two terms are exponents of the term, e, known as Euler’s Number, a mathematical constant used in many circles, including science, engineering, and economics, to calculate a wide variety of things, from bell curves to compound interest rates. It’s a rather esoteric term, much like the term π that’s used to calculate values associated with circles. Euler’s Number was discovered in 1683 by Swiss mathematician Jacob Bernoulli, but oddly enough was named after Leonhard Euler. Its value, 2.718, was determined while Bernoulli manipulated high level mathematics to calculate compound interest rates. If you’d like to learn more about that, follow this link. The term μ is known as the friction coefficient. It quantifies the degree of friction, or roughness, present between the belt and pulley where they make contact. It’s a specific number that remains constant for a given combination of materials. For example, according to Marks’ Standard Handbook for Mechanical Engineers, the value of μ for a leather belt operating on an iron pulley is 0.38. The numerical values for these coefficients were determined over the last few centuries by engineers conducting laboratory testing on various belt and pulley materials. They’re now routinely found in a variety of engineering texts and handbooks. Finally, the term θ denotes the angle of wrap that the belt makes while in contact with the face of the pulley. In our example illustration above, θ measures the arc that’s formed by the belt riding along the surface of the pulley between points A and B, as shown by dotted lines. The angle of wrap is important to overall functionality of the assembly, because the proper amount of friction will allow the pulley-belt assembly to operate efficiently and without slippage. Next time we’ll present an example and use the Euler-Eytelwein Formula to calculate optimal belt friction within a pulley-belt assembly.
Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |