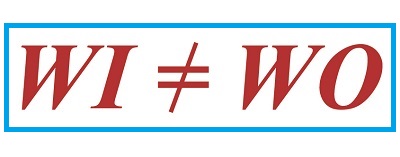|
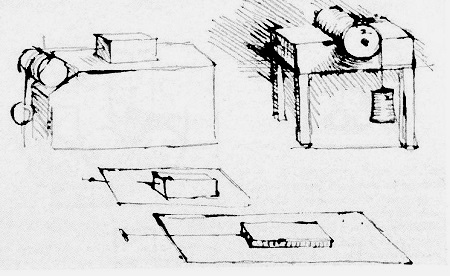
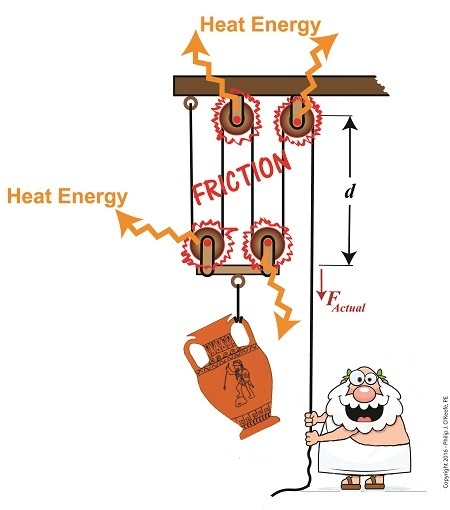
We left off last time with an engineering analysis of energy factors within a compound pulley scenario, in our case a Grecian man lifting an urn. We devised an equation to quantify the amount of work effort he exerts in the process. That equation contains two terms, one of which is beneficial to our lifting scenario, the other of which is not. Today we’ll explore these two terms and in so doing show how there are situations when work input does not equal work output.
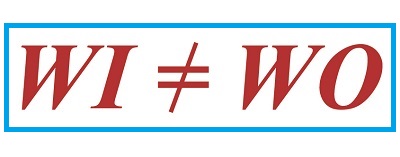
Work Input Does Not Equal Work Output
Here again is the equation we’ll be working with today,
WI = (F × d) + (FF × d) (1)
where, F is the entirely positive force, or work, exerted by human or machine to lift an object using a compound pulley. It represents an ideal but not real world scenario in which no friction is present within the pulley assembly.
The other force at play in our lifting scenario, FF, is less obvious to the casual observer. It’s the force, or work, which must be employed over and above the initial positive force to overcome the friction that’s always present between moving parts, in this case a rope moving through pulley wheels. The rope length extracted from the pulley to lift the object is d.
Now we’ll use this equation to understand why work input, WI, does not equal work output, WO, in a compound pulley arrangement where friction is present.
The first term in equation (1), (F × d), represents the work input as supplied by human or machine to lift the object. It is an idealistic scenario in which 100% of energy employed is directly conveyed to lifting. Stated another way, (F × d) is entirely converted into beneficial work effort, WO.
The second term, (FF × d), is the additional work input that’s needed to overcome frictional resistance present in the interaction between rope and pulley wheels. It represents lost work effort and makes no contribution to lifting the urn off the ground against the pull of gravity. It represents the heat energy that’s created by the movement of rope through the pulley wheels, heat which is entirely lost to the environment and contributes nothing to work output. Mathematically, this relationship between WO, WI, and friction is represented by,
WO = WI – (FF × d) (2)
In other words, work input is not equal to work output in a real world situation in which pulley wheels present a source of friction.
Next time we’ll run some numbers to demonstrate the inequality between WI and WO.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |