|
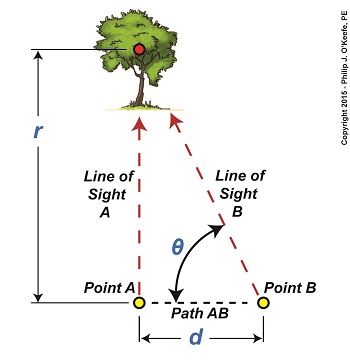
We’ve been working on a way to calculate the distance to a tree situated blocks from our viewing point. Flying raptors, such as our beloved bald eagle, wouldn’t find this in the least bit challenging. They’re able to accurately judge distances due to their special shape-shifting eye lenses which are capable of actually changing curvature spontaneously. But human physiology isn’t equipped for this task, so we’ll have to employ other methods. Today we’ll see how a branch of mathematics known as trigonometry comes into play. Referring to the illustration, we’d like to calculate the distance, r. You’ll note that a right triangle is formed by Line of Sight A, Path AB, and Line of Sight B. As mentioned in our last blog, right triangles are special because the relationship that exists between their sides and their internal angles is well defined within mathematics. In fact, we can calculate r by using this trigonometric formula, r = d × tan(θ) where d is the length of Path AB, θ is the angle between Line of Sight B and Path AB, and tan(θ) is the trigonometric function known as the tangent. Tangent, and other trigonometric functions like sine and cosine, relate the angles in a right triangle to the ratios of the lengths of the sides of the triangle. If we know two of the variables present in the equation presented above, we can determine the third, and the fact that there’s a right triangle present makes that task so much easier. As things stand now we have two unknowns, d and θ. As pointed out last week, the distance, d, is short, so we’ll use a tape measure to determine its length. Let’s say it measures out to be three feet. Now we need to solve for the angle θ that’s formed between Path AB and Line of Sight B. That’s a bit more challenging. There are a number of devices that can be used to measure θ, including a handheld magnetic compass. However, using a compass often yields inaccurate results, thereby increasing the likelihood of mistakes. A more accurate device to use would be an optical rangefinder, as shown below. The optical rangefinder is a device that’s often used in the military to measure long distances by using the principle of parallax. It functions much like binoculars do, but with a twist, literally, as we’ll see next time. ____________________________________
|
Archive for January, 2015
Parallax and Trigonometry
Monday, January 26th, 2015Using Parallax to Measure Distance
Monday, January 19th, 2015|
Last time we introduced an optical effect known as the principle of parallax. Today we’ll get a step closer to seeing how it’s instrumental in measuring distances. For our example we’ll be viewing a point on a tree several blocks away. Since we can’t measure the distance, r, to the tree directly by using a tape measure, we’ll have to use another approach that is made available to us through the principle of parallax. The first step to doing this is to establish two different lines of sight to the red dot on the tree. For our example these will originate at Points A and B, which are both viewing the same spot. Line of Sight A extends straight from Point A to the red spot, while Point B, which is situated only a few feet to the right of A, will provide us with a slanted line of sight to it. We’ll refer to the path between Points A and B as Path AB, which is represented by a black dashed line and has a length, d. You may have noticed from the illustration that Line of Sight B, because it lies on a slant relative to Line of Sight A, provides us with an internal angle, θ, relative to Path AB. This relationship is in fact required to exist if we are to use the principle of parallax, and you’ll see why later. Another requirement is that Path AB must be at a right angle to Line of Sight A, which it is. The illustration bears this out by the fact that a right triangle is formed when Lines of Sight A, B, and Path AB intersect. Right triangles are generally regarded as special within mathematics, but they are particularly special when applying the principle of parallax. The presence of a right triangle enables us to use a branch of mathematics known as trigonometry to correlate the triangle’s angles to the ratios of the lengths of its sides. In other words, we can calculate r by using trigonometry if we are able to measure d and θ. We’ll see how that calculation is done next time. ____________________________________
|
The Principle of Parallax
Thursday, January 8th, 2015|
We’ve been looking at the indirect methods employed by scientists through the ages as they struggled to determine the distance of our Earth from its sun. Today we’ll take a look at one of those indirect methods, known in scientific circles as the Principle of Parallax. Parallax is an optical effect which results in a three dimensional view of the world as seen through our eyes. Because our eyes are spaced a distance apart from each other on the relatively flat surface of our face, each of them will perceive an object along a different line of sight and thus offer differing perspectives. Our brain makes use of the parallax phenomenon to automatically process these differing perspectives into a single image, along with providing us with a three dimensional view of the object, something that comes in handy when negotiating our physical world. As an example, let’s say you’re sitting at the kitchen table staring at a cup of coffee. Your left eye sees the cup from one perspective, your right eye another. To prove it, cover each of your eyes in turn as you look at it. You’ll see that the perspective changes between your two eyes. These two perspectives are processed by your brain into an internal calculation which enables you to adjust your muscle response accordingly. The result is that you are able to deftly pick up the cup of coffee and bring it to your lips rather than clumsily toss it to the floor. Parallax is at work when viewing objects both near and far. Consider Figure 1. Suppose we want to measure the distance from Point A to a tree several blocks away. That’s too far away to use a tape measure, but we can employ the parallax phenomenon and trigonometry, the study of angles, to easily determine the distance. We’ll get a step closer to doing that next time.
____________________________________
|