Posts Tagged ‘falling objects’
Tuesday, March 1st, 2016
|
Objects in motion inevitably meet with opposing forces, a theme which I frequently encounter in my work as an engineering expert. Today we’ll calculate the opposing force our exemplar coffee mug meets when it falls into a pan of kitty litter, thus transforming its freefalling kinetic energy into the work required to move through clay litter.
Let’s revisit the Work-Energy Theorem formula, whose terms were explained in last week’s blog,
F × d = – ½ × m × v12 (1)
The left side of this equation represents the mug’s work to move through the litter, while the right side represents its kinetic energy, which it gained through freefall. To solve for F, the amount of force acting in opposition to the mug’s mass m as it plows a depth d into the litter, we’ll isolate it on one side of the equation, as shown here,
F = [- ½ × m × v12 ] ÷ d (2)
So how do we solve for F when we don’t know the value of v1, the mug’s freefall velocity at impact? We’ll use the fact that The Law of Conservation of Energy tells us that all energies are equal, and we’ll eliminate the part of Equation (2) that contains this unknown variable, that is, the right side of the equation which deals with kinetic energy. In its place we’ll substitute terms which represent the mug’s potential energy, that is, the latent energy held within it as it sat upon the shelf prior to falling. Equation (2) then becomes,
F = [- m × g × h] ÷ d (3)
where g is the Earth’s acceleration of gravity factor, a constant equal to 9.8 meters/sec2 , and h is the height from which the mug fell.
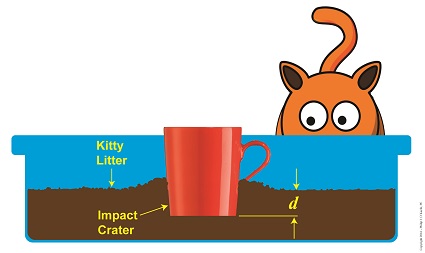
Kinetic Energy Meets With Opposing Force
So if we know the mug’s mass, the distance fallen, and the depth of the crater it made in the litter, we can determine the stopping force acting upon it at the time of impact. It’s time to plug numbers.
Let’s say our mug has a mass of 0.25 kg, it falls from a height of 2 meters, and it makes a crater 0.05 meters deep. Then the stopping force acting upon it is,
F = [- (0.25 kg) × (9.8 meters/sec2) × (2 meters)] ÷ (0.05 meters)
= – 98 Newtons
The mug was subjected to -98 Newtons, or about -22 pounds of opposing force when it fell into the litter, that resistance being presented by the litter itself.
Next time we’ll see what happens when our mug strikes a hard surface that fails to cushion its impact. Energy is released, but where does it go?
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, engineering expert, falling objects, force, kinetic energy, law of conservation of energy, mass, Newtons, potential energy, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on When Kinetic Energy Meets With Opposing Force
Thursday, February 18th, 2016
|
It’s not uncommon in my work as an engineering expert to encounter a situation in which I’m missing information. At that point I’ve got to find a creative solution to working the problem. We’ll get creative today when we combine the Law of Conservation of Energy and the Work-Energy Theorem to get around the fact that we’re missing a key quantity to calculate forces exerted upon the falling coffee mug we’ve been following in this blog series.
Last time we applied the Work-Energy Theorem to our mug as it came to rest in a pan of kitty litter. Today we’ll set up the Theorem formula to calculate the force acting upon it when it meets the litter. Here’s where we left off,
F × d = –½ × m × v12
where, F is the force acting to slow the progress of the mug with mass m inside the litter pan. The mug eventually stops and comes to rest in a crater with a depth, d. The left side of the equation represents the mug’s work expenditure, as it plows through the litter, which acts as a force acting in opposition to the mug’s travel.
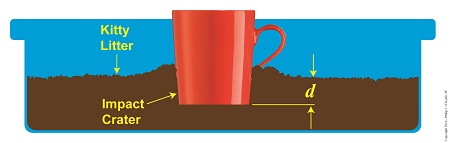
Kinetic Energy Meets Up With Displacement
The right side of the equation represents the mug’s kinetic energy, which it gained in freefall, at its point of impact with the litter. The right side is in negative terms because the mug loses energy when it meets up with this opposing force.
Let’s say we know the values for variables d and m, quantities which are easily measured. But the kinetic energy side of the equation also features a variable of unknown value, v1, the mug’s velocity upon impact. This quantity is difficult to measure without sophisticated electronic equipment, something along the lines of a radar speed detector used by traffic cops. For the purpose of our discussion we’ll say that we don’t have a cop standing nearby to measure the mug’s falling speed.
If you’ll recall from past blog discussions, the Law of Conservation of Energy states that an object’s — in this case our mug’s — kinetic energy is equal to its potential energy. It’s this equivalency relationship which will enable us to solve the equation and work around the fact that we don’t have a value for v1.
We’ll do the math and plug in the numbers next time.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: displacement, engineering expert, falling objects, impact force, kinetic energy, law of conservation of energy, mass, opposing force, potential energy, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Combining the Law of Conservation of Energy and Work-Energy Theorem
Monday, February 8th, 2016
|
So far we’ve applied the Work-Energy Theorem to a flying object, namely, Santa’s sleigh, and a rolling object, namely, a car braking to avoid hitting a deer. Today we’ll apply the Theorem to a falling object, that coffee mug we’ve been following through this blog series. We’ll use the Theorem to find the force generated on the mug when it falls into a pan of kitty litter. This falling object scenario is one I frequently encounter as an engineering expert, and it’s something I’ve got to consider when designing objects that must withstand impact forces if they are dropped.

Applying the Work-Energy Theorem to Falling Objects
Here’s the Work-Energy Theorem formula again,
F × d = ½ × m × [v22 – v12]
where F is the force applied to a moving object of mass m to get it to change from a velocity of v1 to v2 over a distance, d.
As we follow our falling mug from its shelf, its mass, m, eventually comes into contact with an opposing force, F, which will alter its velocity when it hits the floor, or in this case a strategically placed pan of kitty litter. Upon hitting the litter, the force of the mug’s falling velocity, or speed, causes the mug to burrow into the litter to a depth of d. The mug’s speed the instant before it hits the ground is v1, and its final velocity when it comes to a full stop inside the litter is v2, or zero.
Inserting these values into the Theorem, we get,
F × d = ½ × m × [0 – v12]
F × d = – ½ × m × v12
The right side of the equation represents the kinetic energy that the mug acquired while in freefall. This energy will be transformed into Gaspard Gustave de Coriolis’ definition of work, which produces a depression in the litter due to the force of the plummeting mug. Work is represented on the left side of the equal sign.
Now a problem arises with using the equation if we’re unable to measure the mug’s initial velocity, v1. But there’s a way around that, which we’ll discover next time when we put the Law of Conservation of Energy to work for us to do just that.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: energy, engineering expert, falling objects, Gaspard-Gustave de Coriolis, impact forces, kinetic energy, law of conservation of energy, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury | Comments Off on Applying the Work-Energy Theorem to Falling Objects
Friday, September 18th, 2015
|
Last time we introduced kinetic energy as the energy of movement. Today we’ll see how to calculate it, using French mathematician Gaspard-Gustave de Coriolis’ formula as set out in his textbook, Calculation of the Effect of Machines. We’ll then apply his formula to our example of a coffee mug falling from its shelf.
Gaspard-Gustave de Coriolis’ book presented physics concepts, specifically the study of mechanics, in an accessible manner, without a lot of highbrow theory and complicated mathematics. His insights made complicated subjects easy to understand, and they were immediately put to use by engineers of his time, who were busily designing mechanical devices like steam engines during the early stages of the Industrial Revolution.
Within its pages the mathematics of kinetic energy was presented in the scientific form that persists to present day. That formula is,
KE = ½ × m × v2
where m is the moving object’s mass and v its velocity.
In the case of our coffee mug, its kinetic energy will be zero so long as it remains motionless on the shelf. A human arm had lifted it to its perch against the force of gravity, thereby investing it with gravitational potential energy. If the mug was sent freefalling to the ground by the mischievous kitty, its latent potential energy would be realized and converted into the kinetic energy of motion.

To illustrate, let’s say a mug with a mass equal to 0.25 kg rests on a shelf 2 meters above the floor. Its potential energy would then be equal to 4.9 kg • meter2/second2, as was computed in our previous blog, Computing Potential Energy.
Once kitty nudges the mug from its perch and it begins to fall, its latent gravitational potential energy begins a conversion process from potential to kinetic energy. It will continue to convert into an amount of kinetic energy that’s precisely equal to the mug’s potential energy while at rest on the shelf, that is, 4.9 kg • meter2/second2. Upon impact with the floor, all the mug’s gravitational potential energy will have been converted into kinetic energy.
Next time we’ll apply the Law of Conservation of Energy to the potential and kinetic energy formulas to calculate the mug’s velocity as it freefalls to the floor.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: Calculation of the Effect of Machines, engineering expert witness, engines, falling objects, Gaspard-Gustave de Coriolis, kinetic energy, machinery, mass, mechanical energy, mechanical engineer, mechanics, physics, potential energy, velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Calculation of the Effect of Machines — How to Calculate Kinetic Energy
Friday, September 11th, 2015
|
Last time we introduced The Law of Conservation of Energy, which holds that energy can neither be created nor destroyed. We then applied the concept to a mug resting on a shelf, brimming with latent gravitational potential energy. Today we’ll continue our discussion with a focus on kinetic energy and how Willem Gravesande’s experimentation contributed to our understanding of the subject.
The concept of kinetic energy was first posited by mathematicians Gottfried Leibniz and Johann Bernoulli in the early 18th Century when they theorized that the energy of a moving object is a factor of its mass and speed. Their theory was later proven by Willem Gravesande, a Dutch lawyer, philosopher, and scientist.
Gravesande conducted experiments in which he dropped identical brass balls into a soft clay block. See Figure 1.
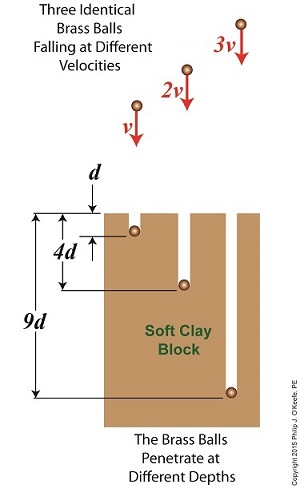
Figure 1
Figure 1 shows the results obtained when balls of the same mass m are dropped from various heights, resulting in different velocities as they fall and different clay penetrations. The ball on the left falls at velocity v and penetrates to a depth d. The center ball falls at twice the left ball’s velocity, or 2v, and penetrates four times as deep, or 4d. The right ball falls at three times the left ball’s velocity, 3v, and it penetrates nine times deeper, 9d. The results indicate an exponential increase in clay penetration, dependent on the balls’ speed of travel.
In fact, all the kinetic energy that the balls exhibited during freefall was converted into mechanical energy from the instant they impacted the clay until their movement within it stopped. This change in forms of energy from kinetic to mechanical demonstrates what Julius Robert von Mayer had in mind when he derived his Law of Conservation of Energy. For a refresher on the subject, see last week’s blog, The Law of Conservation of Energy.
As a result of his experimentation, Gravesande was able to conclude that the kinetic energy of all falling objects is a factor of their mass multiplied by their velocity squared, or m × v2.
We’ll see next time how Gravesande’s work paved the way for later scientists to devise the actual formula used to calculate kinetic energy and then we’ll apply it all to our coffee mug falling from the shelf.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: falling objects, forensic engineer, Gottfried Leibniz, impact, Johann Bernoulli, Julius Robert von Mayer, kinetic energy, mass, mechanical energy, mechanical engineering expert witness, penetration, potential energy, velocity, Willem Gravesande
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Willem Gravesande’s Experimentation on Kinetic Energy
Wednesday, September 2nd, 2015
|
Last time we calculated the potential energy hidden within a coffee mug resting on a shelf. The concept of a passive object possessing energy may not be something all readers can identify with, but the secret behind that mug’s latent energy lies within The Law of Conservation of Energy, the topic we’ll be discussing today.
Julius Robert von Mayer, a German physicist of the mid 19th Century, is the man behind the Law. He posited that energy cannot be created or destroyed, it can only be transferred from one object to another or converted from one form of energy to another. Forms of energy include potential, kinetic, heat, chemical, mechanical, and electrical, all of which have the ability to become another form of energy.
Let’s take our coffee mug for example. Where did its potential energy come from? Ultimately, from the radiant energy emitted by the sun. The sun’s radiant energy was absorbed by plants and then converted to chemical energy through the process of photosynthesis, enabling them to grow. When they were later eaten by humans and other animals, the plants’ chemical energy became incorporated into their bodies’ cells, including the arm muscles used to lift the mug to the shelf.
In the act of lifting the cup, the arm’s muscle cells converted their own chemical energy into mechanical energy. And because lifting a mug to a shelf is work, for some of us greater than others, some of the arm’s chemical energy became heat energy which was lost to the environment.
Because of the elevated perch provided to the mug by the arm, which was in direct defiance of Earth’s gravitational pull, the arm muscles’ mechanical energy was transferred to the mug and converted to latent potential energy, because without that shelf to support it, the mug would fall to the ground. The mug’s potential energy would realize its full potential if it should be sent crashing to the floor, at which time it would become another form of energy. The mischievous orange kitty seems to have just that in mind.

We’ll talk more about the mug’s potential energy being converted to other forms next time.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: chemical energy, engineering expert witness, falling objects, gravity, kinetic energy, law of conservation of energy, mechanical energy, potential energy, radiant energy, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Law of Conservation of Energy
Tuesday, August 25th, 2015
|
Last week we discovered that objects acquire potential energy as it relates to gravity based on the height those objects are elevated above the ground. We also introduced an equation to calculate the potential energy of a coffee mug perched on a shelf. We’ll work with that equation today and compute the latent energy that’s hidden within that mug.
Here again is the equation to determine potential energy, put in terms relating to gravity,
PEgravitational = m × g × h
where m is the mass of the mug, h is the height it’s been elevated above the floor, and g is the Earth’s acceleration of gravity factor, as explained in my previous blog entitled, Sir Isaac Newton and the Acceleration of Gravity.
The equation above can be solved using either English or metric units. In the US it’s generally standard practice to perform calculations using English units, such as feet and pounds. But when measuring mass a less familiar English unit, the slug, comes into play. If you’re interested in learning more about this unit, go to a previous blog article entitled, The Force of Gravity.
The kilogram is the metric equivalent of a slug. Since it’s the unit of mass most commonly used throughout the world, we’ll use it to perform our calculation.
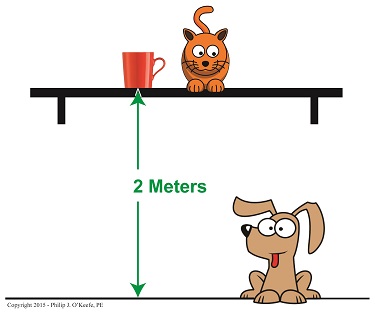
Let’s say our mug has a mass of 0.25 kilograms, the shelf it’s resting on is 2 meters above the floor, and g is 9.8 meters/second2. The mug’s gravitational potential energy would then be expressed as,
PEgravitational = (0.25 kg) × (9.8 meters/second2) × (2 meters)
PEgravitational = 4.9 kg • meter2/second2
Next time we’ll expand on our discussion of potential energy and discuss the Law behind the phenomenon and the fact that energy can only be converted from one form to another.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: acceleration of gravity, engineering expert witness, falling objects, forensic engineer, joule, kilogram, mass, potential energy mechanical engineering expert witness, slug
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Computing Potential Energy
Monday, August 17th, 2015
|
Last week we concluded our discussion on the force of gravity within our solar system. Today we’ll turn our attention to the subject of gravity on Earth and exploring the physics behind falling objects. We’ll start off by discussing potential energy as it relates to gravity, or the latent energy acquired by an object when it’s been elevated above ground level.
Potential energy was the term adopted by 19th Century Scottish scientist William Rankine to represent the latent, or masked, energy hidden within objects. As an example, let’s say you’ve placed your favorite coffee mug in its designated spot on the kitchen shelf. Sitting there so still you wouldn’t dream it was brimming with gravitational potential energy, but if your cat came along and brushed against it, sending it freefalling to the floor, your mug would quickly become a projectile, gaining speed at a uniform rate as it accelerated towards ground level.
Where did that once passive little cup acquire its mounting energy? Simply by virtue of the fact it had been lifted by your arm and placed in an elevated position. You see, Earth’s gravitational pull is forever exerting its invisible tug on objects. It was tugging at the mug as you lifted it, and the higher you lifted it, the more gravitational potential energy the mug received. Once perched on the shelf it bridled with latent energy, only to be set free when the cat caused it to lose its support.
To illustrate the relationship between the coffee mug, the shelf, and Earth’s gravitational pull, we’ll employ the equation used to compute potential energy, notated in terms of gravity,
PEgravitational = m × g × h
This equation states that the mug’s gravitational potential energy, PEgravitational, is a factor of its mass, m, Earth’s gravitational pull, g, and the mug’s height above ground level, h.
Within the scientific community g is referred to as Earth’s acceleration of gravity, a phenomenon commonly accepted to be the uniform accelerating rate at which an object falls on Earth, equal to 9.8 meters per second per second, or meters/second2. It represents a rate of constant acceleration, which happens to be precisely the same whether the object falling is a brick, feather, or coffee mug.
Next time we’ll work with the potential energy equation which will enable us to see how the curious orange kitty sets loose the latent power held within that mug.

Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: engineering expert witness, falling objects, forensic engineer, gravitational potential energy, gravity, latent energy, potential energy
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Gravitational Potential Energy on Earth
Monday, August 3rd, 2015
|
Last time we discovered that Earth zips around the sun at the mind boggling speed of 29,680 meters per second. This is the final bit of information required to calculate Fg, the gravitational force exerted upon Earth by its sun, as set out in Newton’s equation on the subject and derived from his Second Law of Motion. We’ll calculate that quantity today.
Newton’s formula that we’ll be working with is,
Fg = [m × v2] ÷ r
where Earth’s speed, or orbital velocity, is the v in the equation. The other variables, m and r, have previously been determined in this blog series. For a refresher see Centripital Force Makes the Earth Go Round, What is Earth’s Mass, and Calculating the Distance to the Sun. Earth’s mass, m, is valued at 5.96 × 1024 kilograms, while r is Johannes Kepler’s astronomical unit, equal to about 149,000,000,000 meters.
Inserting these numerical values into Newton’s equation to determine the sun’s gravitational force acting upon Earth we arrive at,
Fg = [(5.96 × 1024 kilograms) × (29,680 meters per second)2] ÷ 149,000,000,000 meters
Fg = 3.52 × 1022 kilogram • meter per second2
This metric unit of force, kilogram • meter per second2, represents kilograms multiplied by meters, and their product divided by seconds squared. It’s known in scientific circles as the Newton, in honor of Sir Isaac Newton, widely recognized as one of the greatest scientists of all time and a key figure in the scientific revolution that began over three centuries ago. Therefore the sun’s gravitational force acting upon Earth is typically referred to as,
Fg = 3.52 × 1022 Newtons
Here in the US where we like to use English units such as feet and pounds, the Newton is said to equal 0.225 pounds of force. Therefore in English units the sun’s gravitational force is expressed as,
Fg = (3.52 × 1022 Newtons) × (0.225 pounds of force per Newton)
Fg = 7.93 × 1021 pounds
That’s scientific notation for 7,930,000,000,000,000,000,000 pounds! That’s the amount of force exerted by the sun’s gravitational pull on Earth. Seems about right — right?
Now that we know Fg, we have everything we need to calculate the mass of the sun, which in turn enables us to determine the mass and gravity of other planets in our solar system. We’ll calculate the sun’s mass next time.
____________________________________
|
Tags: engineering expert witness, falling objects, force of gravity, forensic engineer, gravity, mass of the Earth, Newton's Second Law, Sir Isaac Newton, the AU, the sun's gravitational force
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Sun’s Gravitational Force
Thursday, June 18th, 2015
|
We left off with Edmund Halley’s proposed method to solve the riddle of Earth’s distance to the sun. Halley posited that when Venus’ orbit brought it directly between the Earth and sun, then principles of astronomy, trigonometry, and geometry could be combined to calculate that distance. Instrumental to Halley’s theory were a number of elements discussed previously in this blog series, including the work of Johannes Kepler. We’ll mesh those elements today and chart the course for future discoveries.
To begin things, Halley knew that Kepler’s Third Law of Planetary Motion set out the distance between Earth and the sun in theoretical terms as,
1AU = rVenus ÷ 0.28
which meant that if the distance from Earth to Venus, rVenus, could be calculated, then the distance from Earth to the sun was easily deduced, a matter of simple division.
Crucial to the calculation of rVenus is to find the value for the angle α which forms between observers’ lines of sight while charting Venus’ travel across the face of the sun, something which only happens during a rare astronomical event known as the Transit of Venus. See Figure 1.
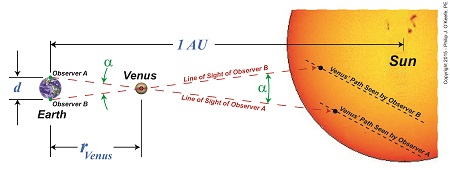
Figure 1
Figure 1 shows two observers positioned on opposite sides of the Earth, busily surveying Venus’ movement across the sun’s face. Their lines of sight converge at a vertex point, or point of intersection, on Venus, then move beyond it to the sun. Due to the principle of vertical angles, which stipulates that angles which share the same vertex point also share the same angle measurement, we know that the angle α that’s formed between Observer A and B‘s lines of sight is of the same value between Earth and Venus as it is between Venus and the sun.
Once a is determined, its numerical value can be plopped into an equation we’ve been working with for some time now in this blog series. It’s similar to the equation previously used to calculate Earth’s distance to the moon,
r = d x tan(θ)
Follow this link to Optically Measuring Cosmic Distances for a review.
And here is that equation with terms modified to reflect our new quest, the distance from Earth to Venus,
rVenus = d ÷ tan(α)
As for the variable d, the distance between the two observers, we’ve worked with that before, too. Follow this link to Determining Chord Length on Circle Earth for a refresher.
Next time we’ll see how Venus’ travel path is key to determining the angle α, shown in green on the illustration, and how this angle is crucial to our discovery of the distance between Earth and the sun.
____________________________________
|
Tags: astronomical unit, chord, distance to the sun, distance to Venus, Edmund Halley, engineering expert witness, falling objects, forensic engineer, geometry, gravity, Johannes Kepler, Kepler's Third Law of Planetary Motion, parallax, the AU, Transit of Venus, trigonometry
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property | Comments Off on Earth’s Distance to the Sun — A Roadmap













