|
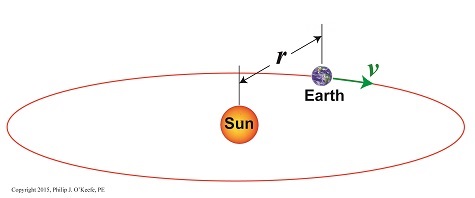
Last time we introduced Newton’s equation to calculate the sun’s gravitational force acting upon Earth, and today we’ll begin solving for the last remaining unsolved variable within that equation, v, Earth’s orbital velocity. Here again is Newton’s equation, Fg = [m × v2] ÷ r For a refresher on how we solved for m, Earth’s mass, and r, the distance between Earth and the sun, follow these links to past blogs in this series, What is Earth’s Mass and Calculating the Distance to the Sun. Velocity, or speed, as it’s most commonly referred to, is based on both time and distance. To bear this out we’ll use an object and situation familiar to all of us, traveling in a car. The car’s velocity is a factor of both the distance traveled and the time it takes to get there. A car traveling at a velocity of 30 miles per hour will cover a distance of 30 miles in one hour’s time. This relationship is borne out by the formula, vCar = distance traveled ÷ travel time vCar = 30 miles ÷ 1 hour = 30 miles per hour Similarly, v is the distance Earth travels during its orbital journey around the sun within a specified period of time. It had been observed since ancient times that it takes Earth one year to complete one orbit, so all that remained to be done was calculate the distance Earth traveled during that time. Vital to calculations was the fact that Earth’s orbit is a circle, which allows geometry to be employed and calculations to be thereby simplified. Refer to Figure l. Figure 1 From geometry we know that the circumference of a circle, C, is calculated by, C = 2× π × r where π is a constant, the well known mathematical term pi, which is equal to 3.1416, and r is the radius of Earth’s circular orbit, determined, courtesy of the work of Johannes Kepler and Edmund Halley, to be approximately 93,000,000 miles. Stated in metric units, the unit of measurement most often employed in science, that comes to 149,000,000,000 meters. Inserting these numerical values for π and r into the circumference formula, scientists calculated the distance Earth travels in one orbit around the sun to be, C = 2 × π × 149,000,000,000 meters = 9.36 x 1011 meters Next time we’ll introduce the time element into our equations and solve for v, and from there we’ll go on and finally solve for Fg, the sun’s gravitational force acting upon Earth.
____________________________________
|
Posts Tagged ‘Edmund Halley’
Earth’s Orbital Velocity
Sunday, July 19th, 2015Earth’s Distance to the Sun — A Roadmap
Thursday, June 18th, 2015|
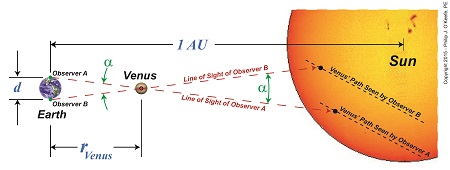
We left off with Edmund Halley’s proposed method to solve the riddle of Earth’s distance to the sun. Halley posited that when Venus’ orbit brought it directly between the Earth and sun, then principles of astronomy, trigonometry, and geometry could be combined to calculate that distance. Instrumental to Halley’s theory were a number of elements discussed previously in this blog series, including the work of Johannes Kepler. We’ll mesh those elements today and chart the course for future discoveries. To begin things, Halley knew that Kepler’s Third Law of Planetary Motion set out the distance between Earth and the sun in theoretical terms as, 1AU = rVenus ÷ 0.28 which meant that if the distance from Earth to Venus, rVenus, could be calculated, then the distance from Earth to the sun was easily deduced, a matter of simple division. Crucial to the calculation of rVenus is to find the value for the angle α which forms between observers’ lines of sight while charting Venus’ travel across the face of the sun, something which only happens during a rare astronomical event known as the Transit of Venus. See Figure 1. Figure 1 Figure 1 shows two observers positioned on opposite sides of the Earth, busily surveying Venus’ movement across the sun’s face. Their lines of sight converge at a vertex point, or point of intersection, on Venus, then move beyond it to the sun. Due to the principle of vertical angles, which stipulates that angles which share the same vertex point also share the same angle measurement, we know that the angle α that’s formed between Observer A and B‘s lines of sight is of the same value between Earth and Venus as it is between Venus and the sun. Once a is determined, its numerical value can be plopped into an equation we’ve been working with for some time now in this blog series. It’s similar to the equation previously used to calculate Earth’s distance to the moon, r = d x tan(θ) Follow this link to Optically Measuring Cosmic Distances for a review. And here is that equation with terms modified to reflect our new quest, the distance from Earth to Venus, rVenus = d ÷ tan(α) As for the variable d, the distance between the two observers, we’ve worked with that before, too. Follow this link to Determining Chord Length on Circle Earth for a refresher. Next time we’ll see how Venus’ travel path is key to determining the angle α, shown in green on the illustration, and how this angle is crucial to our discovery of the distance between Earth and the sun.
____________________________________
|
The Transit of Venus
Monday, May 18th, 2015|
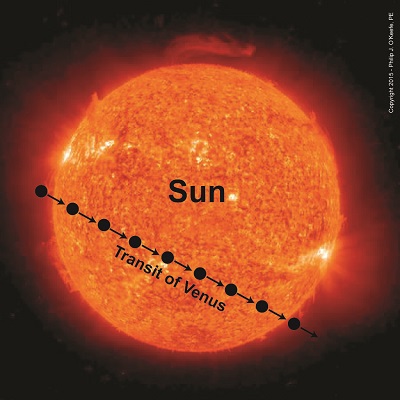
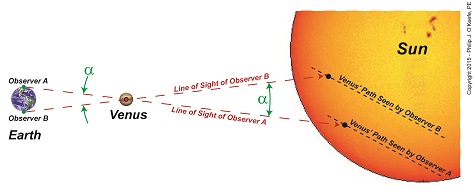
Last time we learned of Johannes Kepler’s Third Law of Planetary Motion and his development of the astronomical unit (AU) and how these contributed to bringing ancient scientists a step closer to calculating Earth’s distance to the sun. Today we’ll see why Kepler’s focus on Venus, specifically its travel through space in relation to Earth and the sun — the so-called transit of Venus — would become the crucial element to solving the puzzle. Astronomers had previously used the Earth itself as an optical rangefinder to calculate distance to the moon. But unlike the moon which is relatively close to Earth, the sun is many tens of millions of miles away, too distant to be used in that manner. When it came to finding the distance from Earth to its sun, they were stumped. Then in 1716 Edmund Halley had the insight to combine Kepler’s Third Law and the parallax principle with Venus’ orbital journeys to devise an ingenious solution to the problem. The transit of Venus, first predicted by Kepler in 1627, is a rare astronomical phenomenon which only occurs every 243 years. At this time Venus becomes clearly visible from Earth and appears as a black dot traveling a straight path across the fiery backdrop of the sun’s surface. Figure 1 shows this phenomenon as it would look from Earth. According to Halley’s plan, two observers with telescopes would be positioned on opposite sides of the Earth. Due to the principle of parallax their lines of sight would provide different perspectives of Venus’ path. See Figure 2. From the perspective of Observer B, Venus’s path would appear higher on the sun’s face than the path seen from the perspective of Observer A. As their lines of sight converge on Venus’ center, an angle forms between them, which we’ll name α. The same angle forms as they look past Venus to the sun in its backdrop. Halley theorized that if the angle α could be measured, Kepler’s Third Law could be used together with trigonometry to calculate the distance between Earth and the sun, Kepler’s so-called AU. We’ll review Halley’s methodology next time.
____________________________________
|
Optically Measuring Cosmic Distances
Wednesday, April 22nd, 2015|
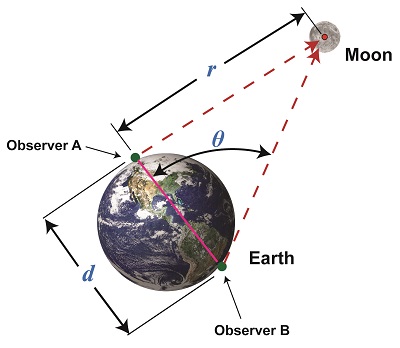
Last time we learned that the bigger an optical rangefinder, the better its accuracy in measuring distant objects. Today we’ll take that concept a step further when we discover how Earth itself was used by ancient scientists to gauge its distance to the moon. Today’s blog will be strewn with embedded links to past blogs in this series, all of which have been building up to our understanding of gravity, a complex subject with many pieces to its puzzle. There are a few remaining pieces to be placed which will be covered in future blogs, but I promise we’ll get there. Long before Edmund Halley’s time, scientists used the Earth as a huge optical rangefinder. In doing so they employed the principles of parallax and trigonometry to obtain reasonably accurate measurements of the distance between Earth and its nearest neighbors, starting with the moon. See Figure 1. The illustration shows how it was done. Two observers armed with telescopes viewed the moon from opposite sides of the earth. Their lines of sight are represented by dashed lines, and together with the solid pink line which represents the distance between them, d, a right triangle was formed. Because Observer B was situated on the other side of the globe, his line of sight fell at an angle relative to Observer A’s, due to the Principle of Parallax. The angle that formed at the point in the triangle at which B was situated we’ll call θ. The fact that a right triangle was formed at Observer A’s observation point will enable our ancient scientists to use principles of trigonometry and parallax in their quest to find the distance to the moon. Follow this link to a refresher blog on the subject, Using Parallax to Measure Distance. At precisely the same moment the moon moved into Observer A’s telescopic line of sight, Observer B adjusted his telescope to center the moon within it. Observer B then duly measured the angle θ formed with a protractor, just as would be done with a rangefinder. If you’ve been reading along in this series, this setup might look familiar to you. In fact, the two mirrors of a military optical rangefinder work in exactly the same way as our two observers looking at the moon. Follow this link to a refresher on the internal workings of a rangefinder. Once the angle θ’s value had been determined, it was used to calculate the distance r between Earth and the moon with the same equation we’ve been using to measure distances using military optical rangefinders: r = d × tan(θ) As far as our moon observers go, the only variable left for them to determine before they are able to measure Earth’s distance to the moon is d, the distance between their viewing positions on Earth. We’ll see how to solve for d next time, when we put the Earth’s geometry to work for us.
____________________________________
|
Kepler’s Third Law Of Planetary Motion
Wednesday, December 31st, 2014|
Edmund Halley was faced with a real puzzle when he began his quest to determine the distance of Earth from the sun. One of the pieces to solving that puzzle came from the work of a German mathematician, astronomer and astrologer named Johannes Kepler. Early in the 17th Century, Kepler spent a lot of time observing the planets in our solar system as they orbited the sun. He discovered that by taking note of the time it took for a planet to make one orbit around the sun, he could determine its relative distance from it. He then compared his findings with other planets, noting the time it took for each to make this same journey. His discovery would come to be known as Kepler’s Third Law of Planetary Motion. But what exactly is meant by a planet’s “relative distance from the sun”? In essence, it means that interplanetary distances, like just about everything else, are relative. Put another way, heavenly bodies can be said to be a distance X relative to another heavenly body if you establish a value for X, whether it’s numerical or otherwise. In Kepler’s case, X would be the unknown value of a so-called astronomical unit (AU), where one AU is equal to the unknown distance from Earth to the sun. Represented in equation form, this distance is: rEarth-sun = 1 AU This relative marker of distance could then be used to show how far the other planets are from the sun, relative to Earth’s distance from the sun, the AU. Kepler’s astronomical unit is simply a placeholder term for an unknown quantity, similar to any other unknown variable that might be used in an algebraic equation. For example, Kepler observed the orbits of Venus and Mars and determined their relative distances to the sun to be: rVenus-sun = 0.72 × 1 AU = 0.72 AU rMars-sun = 1.5 × 1 AU = 1.5 AU In other words, Venus’ distance from the sun is just under three quarters of Earth’s and Mars is one and a half times Earth’s distance from the sun. In this way, Kepler was able to determine the relative distances from the sun in AU for all the observable planets in our solar system. Kepler felt sure that one day scientists would be able to accurately measure Earth’s distance from the sun, and when they accomplished this they could employ his astronomical unit system to determine distances between other planets in our solar system and the sun. Next time we’ll introduce the principle of parallax and see how Halley used this optical effect to devise a method for assigning a value to Kepler’s unknown AU. ____________________________________ |
How Far Away is the Sun?
Wednesday, December 24th, 2014|
Astronomers tell us that the sun is approximately 93,000,000 miles from Earth. Since no direct method of measuring this distance exists, how did scientists determine this? They had to resort to indirect methods. In the early 18th Century, British astronomer, mathematician and physicist Edmund Halley, of Halley’s Comet fame, devised a method to measure the distance between Earth and its sun with reasonable accuracy. His method was based in part on an optical effect known as the principle of parallax, which had been discovered more than 2000 years ago by Greek astronomer Hipparchus when he also employed it to try and determine that same distance. Halley also employed the ideas of 17th Century German mathematician, astronomer, and astrologist Johannes Kepler. Kepler’s work on planetary motion, in particular the geometry of planetary orbits in our solar system, were vital to Halley’s distance measuring method. Next time we’ll see how Kepler’s Third Law of Planetary Motion brought Halley one step closer to methodology that would determine the distance of our home planet to its sun. _______________________________________
|