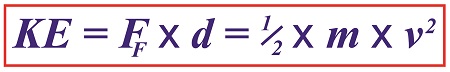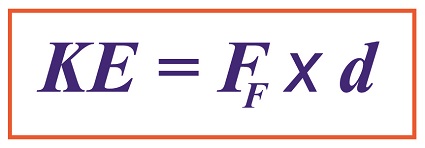Posts Tagged ‘velocity’
Monday, August 14th, 2017
|
Last time we introduced the Mechanical Power Formula, which is used to compute power in pulley-belt assemblies, and we got as far as introducing the term tangential velocity, V, a key variable within the Formula. Today we’ll devise a new formula to compute this tangential velocity.
Our starting point is the formula introduced last week to compute the amount of power, P, in our pulley-belt example is, again,
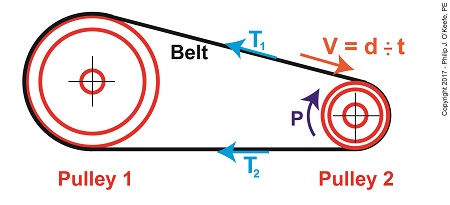
P = (T1 – T2) × V (1)
We already know that P is equal to 4 horsepower, we have yet to determine the belt’s tight side tension, T1, and loose side tension, T2, and of course V, the formula for which we’ll develop today.
Tangential Velocity
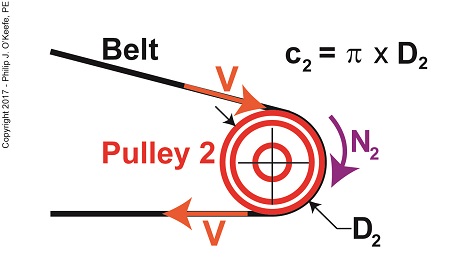
Tangential velocity is dependent on both the circumference, c2, and rotational speed, N2, of Pulley 2. The circumference represents the length of Pulley 2’s curved surface. The belt travels part of this distance as it makes its way from Pulley 2 back to Pulley 1. The rotational speed, N2, represents the rate that it takes for Pulley 2’s curved surface to make one revolution while propelling the belt. This time period is known as the period of revolution, t2, and is related to N2 by this equation,
N2 = 1 ÷ t2 (2)
The rotational speed of Pulley 2 is specified in our example as 300 RPMs, or revolutions per minute, and we’ll denote that speed as N2 in light of the fact it’s referring to speed present at the location of Pulley 2. As we build the formula, we’ll be converting N2 into velocity, specifically tangential velocity, V, which is the velocity at which the belt operates, this in turn will enable us to solve equation (1).
Why speak in terms of tangential velocity rather than plain old ordinary velocity? Because the moving belt’s orientation to the surface of the pulley lies at a tangent in relation to the pulley’s circumference, c2, as shown in the above illustration. Put another way, the belt enters and leaves the curved surface of the pulley in a straight line.
Generally speaking, velocity is distance traveled over a period of time, and tangential velocity is no different. So taking time into account we arrive at this formula,
V = c2 ÷ t2 (3)
Since the surface of Pulley 2 is a circle, its circumference can be computed using a formula developed thousands of years ago by the Greek engineer and mathematician Archimedes. It is,
c2 = π × D2 (4)
where D2 is the diameter of the pulley and π represents the constant 3.1416.
We now arrive at the formula for tangential velocity by combining equations (3) and (4),
V = π × D2 ÷ t2 (5)
Next time we’ll plug numbers into equation (5) and solve for V.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, belt velocity, circumference, engineer, loose side tension, mechanical power formula, period of revolution, pulley, pulleys, speed, tangential velocity, tight side tension, velocity
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Tangential Velocity
Saturday, July 29th, 2017
|
Last time we determined the value for one of the key variables in the Euler-Eytelwein Formula known as the angle of wrap. To do so we worked with the relationship between the two tensions present in our example pulley-belt assembly, T1 and T2. Today we’ll use physics to solve for T2 and arrive at the Mechanical Power Formula, which enables us to compute the amount of power present in our pulley and belt assembly, a common engineering task.
To start things off let’s reintroduce the equation which defines the relationship between our two tensions, the Euler-Eytelwein Formula, with the value for e, Euler’s Number, and its accompanying coefficients, as determined from our last blog,
T1 = 2.38T2 (1)
Before we can calculate T1 we must calculate T2. But before we can do that we need to discuss the concept of power.
The Mechanical Power Formula in Pulley and Belt Assemblies
Generally speaking, power, P, is equal to work, W, performed per unit of time, t, and can be defined mathematically as,
P = W ÷ t (2)
Now let’s make equation (2) specific to our situation by converting terms into those which apply to a pulley and belt assembly. As we discussed in a past blog, work is equal to force, F, applied over a distance, d. Looking at things that way equation (2) becomes,
P = F × d ÷ t (3)
In equation (3) distance divided by time, or “d ÷ t,” equals velocity, V. Velocity is the distance traveled in a given time period, and this fact is directly applicable to our example, which happens to be measured in units of feet per second. Using these facts equation (3) becomes,
P = F × V (4)
Equation (4) contains variables that will enable us to determine the amount of mechanical power, P, being transmitted in our pulley and belt assembly.
The force, F, is what does the work of transmitting mechanical power from the driving pulley, pulley 2, to the passive driven pulley, pulley1. The belt portion passing through pulley 1 is loose but then tightens as it moves through pulley 2. The force, F, is the difference between the belt’s tight side tension, T1, and loose side tension, T2. Which brings us to our next equation, put in terms of these two tensions,
P = (T1 – T2) × V (5)
Equation (5) is known as the Mechanical Power Formula in pulley and belt assemblies.
The variable V, is the velocity of the belt as it moves across the face of pulley 2, and it’s computed by yet another formula. We’ll pick up with that issue next time.
Copyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: belt, distance divided by time, engineering, Euler-Eytelwein Formula, Euler's Number, force, loose side tension, mechanical power, mechanical power formula, power, power transmitted, pulley, tight side tension, velocity, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Mechanical Power Formula in Pulley and Belt Assemblies
Monday, June 6th, 2016
|
As an engineering expert, I often use the fact that formulas share a single common factor in order to set them equal to each other, which enables me to solve for a variable contained within one of them. Using this approach we’ll calculate the velocity, or speed, at which the broken bit of ceramic from the coffee mug we’ve been following slides across the floor until it’s finally brought to a stop by friction between it and the floor. We’ll do so by combining two equations which each solve for kinetic energy in their own way.
Last time we used this formula to calculate the kinetic energy, KE, contained within the piece,
KE = FF × d (1)
and we found that it stopped its movement across the floor when it had traveled a distance, d, of 2 meters.
We also solved for the frictional force, FF, which hampered its free travel, and found that quantity to be 0.35 kilogram-meters/second2. Thus the kinetic energy contained within that piece was calculated to be 0.70 kilogram-meters2/second2.
Now we’ll put a second equation into play. It, too, provides a way to solve for kinetic energy, but using different variables. It’s the version of the formula that contains the variable we seek to calculate, v, for velocity. If you’ll recall from a previous blog, that equation is,
KE = ½ × m × v2 (2)
Of the variables present in this formula, we know the mass, m, of the piece is equal to 0.09 kilograms. Knowing this quantity and the value derived for KE from formula (1), we’ll substitute known values into formula (2) and solve for v, the velocity, or traveling speed, of the piece at the beginning of its slide.
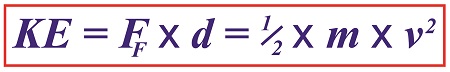
Combining Kinetic Energy Formulas to Calculate Velocity
The ceramic piece’s velocity is thus calculated to be,
KE = ½ × m × v2
0.70 kilogram-meters2/second2= ½ × (0.09 kilograms) × v2
now we’ll use algebra to rearrange things and isolate v to solve for it,
v2 = 2 × (0.70 kilogram-meters2/second2) ÷ (0.09 kilograms)
v = 3.94 meters/second =12.92 feet/second = 8.81 miles per hour
Our mug piece therefore began its slide across the floor at about the speed of an experienced jogger.

This ends our series on the interrelationship of energy and work. Next time we’ll begin a new topic, namely, how pulleys make the work of lifting objects and driving machines easier.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, energy, engineering expert, friction, frictional force, kinetic energy, mass, velocity, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Combining Kinetic Energy Formulas to Calculate Velocity
Wednesday, May 25th, 2016
|
My activities as an engineering expert often involve creative problem solving of the sort we did in last week’s blog when we explored the interplay between work and kinetic energy. We used the Work-Energy Theorem to mathematically relate the kinetic energy in a piece of ceramic to the work performed by the friction that’s produced when it skids across a concrete floor. A new formula was derived which enables us to calculate the kinetic energy contained within the piece at the start of its slide by means of the work of friction. We’ll crunch numbers today to determine that quantity.
The formula we derived last time and that we’ll be working with today is,
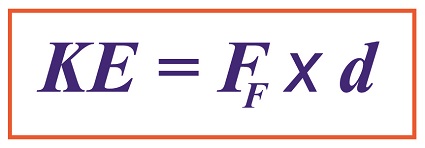 Calculating Kinetic Energy By Means of the Work of Friction
where, KE is the ceramic piece’s kinetic energy, FF is the frictional force opposing its movement across the floor, and d is the distance it travels before friction between it and the less than glass-smooth floor brings it to a stop.
The numbers we’ll need to work the equation have been derived in previous blogs. We calculated the frictional force, FF, acting against a ceramic piece weighing 0.09 kilograms to be 0.35 kilogram-meters/second2 and the measured distance, d, it travels across the floor to be equal to 2 meters. Plugging in these values, we derive the following working equation,
KE = 0.35 kilogram-meters/second2 × 2 meters
KE = 0.70 kilogram-meters2/second2
The kinetic energy contained within that broken bit of ceramic is just about what it takes to light a 1 watt flashlight bulb for almost one second!
Now that we’ve determined this quantity, other energy quantities can also be calculated, like the velocity of the ceramic piece when it began its slide. We’ll do that next time.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, electrical energy, energy, engineering expert, frictional force, kinetic energy, mass, velocity, Watt, work, work of friction, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Calculating Kinetic Energy By Means of the Work of Friction
Thursday, May 12th, 2016
|
We’ve been discussing the different forms energy takes, delving deeply into de Coriolis’ claim that energy doesn’t ever die or disappear, it simply changes forms depending on the tasks it’s performing. Today we’ll combine mathematical formulas to derive an equation specific to our needs, an activity my work as an engineering expert frequently requires of me. Our task today is to find a means to calculate the amount of kinetic energy contained within a piece of ceramic skidding across a concrete floor. To do so we’ll combine the frictional force and Work-Energy Theorem formulas to observe the interplay between work and kinetic energy.
As we learned studying the math behind the Work-Energy Theorem, it takes work to slow a moving object. Work is present in our example due to the friction that’s created when the broken piece moves across the floor. The formula to calculate the amount of work being performed in this situation is written as,
W = FF ×d (1)
where, d is the distance the piece travels before it stops, and FF is the frictional force that stops it.
We established last time that our ceramic piece has a mass of 0.09 kilograms and the friction created between it and the floor was calculated to be 0.35 kilogram-meters/second2. We’ll use this information to calculate the amount of kinetic energy it contains. Here again is the kinetic energy formula, as presented previously,
KE = ½ × m × v2 (2)
where m represents the broken piece’s mass and v its velocity when it first begins to move across the floor.
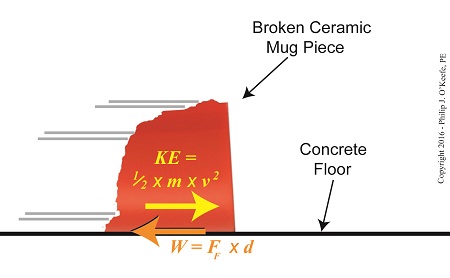
The Interplay of Work and Kinetic Energy
The Work-Energy Theorem states that the work, W, required to stop the piece’s travel is equal to its kinetic energy, KE, while in motion. This relationship is expressed as,
KE = W (3)
Substituting terms from equation (1) into equation (3), we derive a formula that allows us to calculate the kinetic energy of our broken piece if we know the frictional force, FF, acting upon it which causes it to stop within a distance, d,
KE = FF × d
Next time we’ll use this newly derived formula, and the value we found for FF in our previous article, to crunch numbers and calculate the exact amount of kinetic energy contained with our ceramic piece.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, energy, engineering expert, frictional force, kinetic energy, mass, velocity, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Interplay of Work and Kinetic Energy
Thursday, March 24th, 2016
|
Last time we watched our example ceramic coffee mug crash to a concrete floor, where its freefall kinetic energy performed the work of shattering it upon impact. This is a scenario familiar to engineering experts like myself who are sometimes asked to reconstruct accidents and their aftermaths, otherwise known as forensic engineering. Today we’ll take a look at what happens when the shattered mug’s pieces are freed from their formerly cozy, cohesive bond, and we’ll watch their transmutation from kinetic energy to work, and back to kinetic energy.
As we watch our mug shatter on the floor, we notice that it breaks into different sized pieces that are broadcast in many directions around the point of impact. Each piece has its own unique mass, m, travels at its own unique velocity, v, and has a unique and individualized amount of kinetic energy. This is in accordance with the kinetic energy formula, shown here again:
KE = ½ × m × v2
So where did that energy come from?

The Scattering Pieces Have Kinetic Energy
According to the Work-Energy Theorem, the shattered mug’s freefalling kinetic energy is transformed into the work that shatters the mug. Once shattered, that work is transformed back into kinetic energy, the energy that fuels each piece as it skids across the floor.
The pieces spray out from the point of the mug’s impact until they eventually come to rest nearby. They succeed in traveling a fair distance, but eventually their kinetic energy is dissipated due to frictional force which slows and eventually stops them.
The frictional force acting in opposition to the ceramic pieces’ travel is created when the weight of each fragment makes contact with the concrete floor’s rough surface, which creates a bumpy ride. The larger the fragment, the more heavily it bears down on the concrete and the greater the frictional force working against it. With this dynamic at play we see smaller, lighter fragments of broken ceramic cover a greater distance than their heavier counterparts.
The Work-Energy Theorem holds that the kinetic energy of each piece equals the work of the frictional force acting against it to bring it to a stop. We’ll talk more about this frictional force and its impact on the broken pieces’ distance traveled next time.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: engineering expert, force, forensic engineering, friction force, kinetic energy, kinetic energy formula, mass, velocity, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Kinetic Energy to Work, Work to Kinetic Energy
Tuesday, March 1st, 2016
|
Objects in motion inevitably meet with opposing forces, a theme which I frequently encounter in my work as an engineering expert. Today we’ll calculate the opposing force our exemplar coffee mug meets when it falls into a pan of kitty litter, thus transforming its freefalling kinetic energy into the work required to move through clay litter.
Let’s revisit the Work-Energy Theorem formula, whose terms were explained in last week’s blog,
F × d = – ½ × m × v12 (1)
The left side of this equation represents the mug’s work to move through the litter, while the right side represents its kinetic energy, which it gained through freefall. To solve for F, the amount of force acting in opposition to the mug’s mass m as it plows a depth d into the litter, we’ll isolate it on one side of the equation, as shown here,
F = [- ½ × m × v12 ] ÷ d (2)
So how do we solve for F when we don’t know the value of v1, the mug’s freefall velocity at impact? We’ll use the fact that The Law of Conservation of Energy tells us that all energies are equal, and we’ll eliminate the part of Equation (2) that contains this unknown variable, that is, the right side of the equation which deals with kinetic energy. In its place we’ll substitute terms which represent the mug’s potential energy, that is, the latent energy held within it as it sat upon the shelf prior to falling. Equation (2) then becomes,
F = [- m × g × h] ÷ d (3)
where g is the Earth’s acceleration of gravity factor, a constant equal to 9.8 meters/sec2 , and h is the height from which the mug fell.
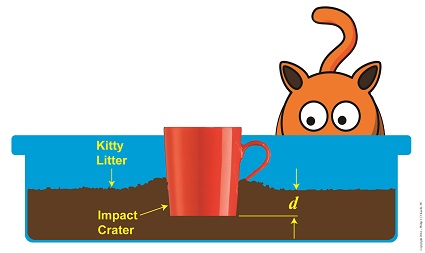
Kinetic Energy Meets With Opposing Force
So if we know the mug’s mass, the distance fallen, and the depth of the crater it made in the litter, we can determine the stopping force acting upon it at the time of impact. It’s time to plug numbers.
Let’s say our mug has a mass of 0.25 kg, it falls from a height of 2 meters, and it makes a crater 0.05 meters deep. Then the stopping force acting upon it is,
F = [- (0.25 kg) × (9.8 meters/sec2) × (2 meters)] ÷ (0.05 meters)
= – 98 Newtons
The mug was subjected to -98 Newtons, or about -22 pounds of opposing force when it fell into the litter, that resistance being presented by the litter itself.
Next time we’ll see what happens when our mug strikes a hard surface that fails to cushion its impact. Energy is released, but where does it go?
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, engineering expert, falling objects, force, kinetic energy, law of conservation of energy, mass, Newtons, potential energy, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on When Kinetic Energy Meets With Opposing Force
Thursday, February 18th, 2016
|
It’s not uncommon in my work as an engineering expert to encounter a situation in which I’m missing information. At that point I’ve got to find a creative solution to working the problem. We’ll get creative today when we combine the Law of Conservation of Energy and the Work-Energy Theorem to get around the fact that we’re missing a key quantity to calculate forces exerted upon the falling coffee mug we’ve been following in this blog series.
Last time we applied the Work-Energy Theorem to our mug as it came to rest in a pan of kitty litter. Today we’ll set up the Theorem formula to calculate the force acting upon it when it meets the litter. Here’s where we left off,
F × d = –½ × m × v12
where, F is the force acting to slow the progress of the mug with mass m inside the litter pan. The mug eventually stops and comes to rest in a crater with a depth, d. The left side of the equation represents the mug’s work expenditure, as it plows through the litter, which acts as a force acting in opposition to the mug’s travel.
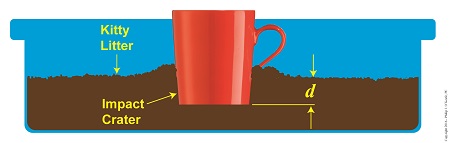
Kinetic Energy Meets Up With Displacement
The right side of the equation represents the mug’s kinetic energy, which it gained in freefall, at its point of impact with the litter. The right side is in negative terms because the mug loses energy when it meets up with this opposing force.
Let’s say we know the values for variables d and m, quantities which are easily measured. But the kinetic energy side of the equation also features a variable of unknown value, v1, the mug’s velocity upon impact. This quantity is difficult to measure without sophisticated electronic equipment, something along the lines of a radar speed detector used by traffic cops. For the purpose of our discussion we’ll say that we don’t have a cop standing nearby to measure the mug’s falling speed.
If you’ll recall from past blog discussions, the Law of Conservation of Energy states that an object’s — in this case our mug’s — kinetic energy is equal to its potential energy. It’s this equivalency relationship which will enable us to solve the equation and work around the fact that we don’t have a value for v1.
We’ll do the math and plug in the numbers next time.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: displacement, engineering expert, falling objects, impact force, kinetic energy, law of conservation of energy, mass, opposing force, potential energy, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Combining the Law of Conservation of Energy and Work-Energy Theorem
Friday, January 29th, 2016
|
I’m sometimes called upon to render an engineering expert opinion on auto accidents, and in our last blog we stretched this application to a scenario in which Santa’s sleigh collided with the opposing force of a strong wind. At that time we used the Work-Energy Theorem to calculate the amount of food energy Rudolph and his team required to regain speed and get back on schedule. Today we’ll use the Theorem to analyze the forces at play in another deer scenario and calculate the braking distance a car needs to avoid hitting one on the highway.
The average sedan has a mass of about 1,500 pounds, or 680 kilograms. In our example it’s driving down the highway at a speed, or velocity, of 30 miles per hour, which equates to it covering a distance of 13.3 meters, or just under 44 feet, per second.
A deer jumps onto the highway, 60 meters in front of the car. The alert driver slams on the brakes, which exert 1200 Newtons of stopping force on the car. If you’ll recall from past blogs in this series, the Newton is the metric unit used to measure force.
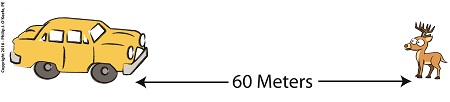 What is Safe Braking Distance? What is Safe Braking Distance?
Did Bambi survive? Let’s use the Work-Energy Theorem to find out. Here it is again,
F × d = ½ × m × [v22 – v12]
where, F is the braking force used to slow a car of mass m, from an initial velocity of v1 to a final velocity of v2 in a braking distance, d. The car will eventually come to a complete stop as the driver attempts to avoid hitting the deer, so its final velocity, v2, will be zero. The Work-Energy Theorem is most often stated in terms of metric units, the measuring unit of choice in the scientific community, and we’ll follow suit with our math.
Inserting these values into the equation, we get,
[1200 Newtons] × d
= ½ × [680 kilograms] × [(0)2 – (13.3 meters per second)2]
Using algebra to solve for d, the braking distance, we arrive at,
d = ½ × [680 kilograms] × [(0)2 – (13.3 meters per second)2] ÷ [1200 Newtons]
d = 50.11 meters
The car stopped 50.11 meters from the point when the driver slammed on his brakes, just about 10 meters short of hitting the deer. Bambi lives to leap another day!
Next time we’ll use the Work-Energy Theorem to assess the fate of the falling coffee mug we introduced in past blogs when we opened our discussion on the different forms of energy.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: automobile, braking distance, braking force, engineering expert, mass, Newtons, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Personal Injury | Comments Off on Applying the Work-Energy Theorem to Braking Distance
Wednesday, January 20th, 2016
|
In my work as an engineering expert I’ve never had to convert Joules of work-energy into calories, but that’s exactly what we’ll be doing together today. Last time we applied the Work-Energy Theorem to the progress of Santa’s sleigh and found that an opposing wind force of 3848.7 Newtons –or 865.2 pounds for those of us who are American– slowed his team from an initial velocity of 90 meters per second to a final velocity of 40 meters per second and that it happened over a distance of 760 meters. Today we’ll see how many calories the reindeer need to expend to get them back up to full delivery speed.

Prancer Loves Oats
Now we know that Santa successfully made all his deliveries on time this past Christmas, so that means that at some point his reindeer team was able to get back up to full sleigh-flying speed. They did it by expending extra energy. We’ll use the Work-Energy Theorem to find out how much energy that equates to. Here’s the Theorem again,
W = ½ × m × [v22 – v12]
where W is the work/energy required to speed up the sleigh team’s mass, m, from an initial velocity v1 to a final velocity v2. For a refresher on the special relationship between work and energy, see our past blog on the subject.
If Santa’s sleigh has a mass of 900 kilograms and its speed must increase from 40 to 90 meters per second, then the work required to do so is calculated as,
W = ½ × (900 kilograms) × [(90 meters/second)2 – (40 meters/second)2]
W = ½ × (900 kilograms) × (6,500 meters2/second2)
W = 2,925,000 kilogram2 · meters2 per second2 = 2,925,000 Joules
So Rudolph and his buddies had to expend 2,925,000 Joules of energy to perform 2,925,000 Joules of work. To understand where Rudolph and his team got that energy, we must state things in terms of nutritional value, that is, units of calories.
Did you know that 1 calorie is equal to 4,184.43 Joules? Applying that equivalency to our situation we get,
Nutritional Energy Required = (2,925,000 Joules) × (4,184.43 Joules/calorie)
= 699.02 calories
The net result is Santa’s team expended a total of 699.02 calories for all the reindeer to regain their full speed of 90 meters per second. That’s the nutritional energy found in slightly more than one cup of oats. Now everybody knows that Santa takes good care of his reindeer, so undoubtedly they were fed plenty of oats and hay before takeoff. This was stored in their body fat for future, on-demand use.
Sadly, Christmas is over, and it’s time to get back to the more mundane aspects of life. Next time we’ll apply the principles behind the Work-Energy Theorem to calculate the braking force required to stop a car in motion.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: calories, energy, engineering expert, Joules, mass, speed, velocity, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Work and Energy, Speed, and Calories