|
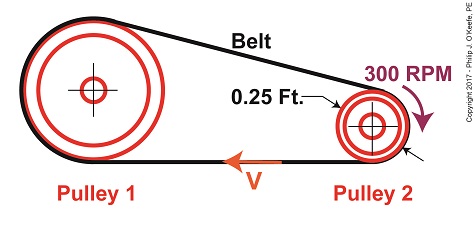
Last time we developed an equation to compute tangential velocity, V, of the belt in our example pulley and belt system. Today we’ll plug numbers into this equation and arrive at a numerical value for this belt velocity. Belt Velocity
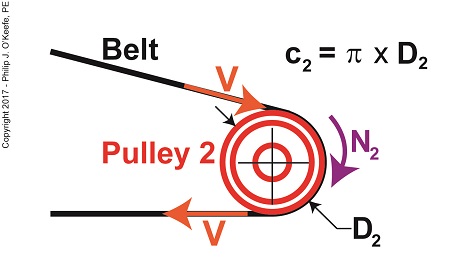
The equation we’ll be working with is, V = π × D2 ÷ t2 (1) where, D2 is the diameter of Pulley 2 and π represents the constant 3.1416. We learned that Pulley 2’s period of revolution, t2, is related to its rotational speed, N2, which represents the time it takes for it to make one revolution and is represented by this equation, N2 = 1 ÷ t2 (2) We’ll now solve for the belt’s velocity, V, using known values, starting off with rearranging terms so we can solve for t2, t2 = 1 ÷ N2 (3) We were previously given that N2 is 300 RPM, or revolutions per minute, so equation (3) becomes, t2 = 1 ÷ 300 RPM = 0.0033 minutes (4) This tells us that Pulley 2 takes 0.0033 minutes to make one revolution in our pulley-belt assembly. Pulley 2’s diameter, D2, was previously determined to be 0.25 feet. Inserting this value equation (1) becomes, V = π × (0.25 feet) ÷ (0.0033 minutes) (5) V = 237.99 feet/minute (6)
We’ve now determined that the belt in our pulley-belt assembly zips around at a velocity of 237.99 feet per minute. Next time we’ll apply this value to equation (6) and determine the belt’s tight side tension, T1. Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |