Posts Tagged ‘tangential velocity’

Tangential Velocity Dangers

Monday, August 28th, 2017

    We’ve been discussing tangential velocity within the context of a pulley and belt assembly in recent blogs, and you may have wondered whether you encounter this phenomenon in your everyday life.  Undoubtedly you have. Have you ever driven a long stretch of highway at a fast clip and suddenly come upon a curve in the road posted at a lower speed limit?  If you happened not to notice the speed reduction, you may have found yourself slamming on the brakes to regain control of your car.  You’ve been caught in a tangential velocity danger zone.

Tangential Velocity Dangers

Tangential Velocity Dangers

   

    As this road sign indicates, cyclists must also beware of potentially dangerous circumstances involving tangential velocity.   It warns of an upcoming drop in the road, which, depending on their speed, has the potential to catapult them into the air.

    Next time we’ll resume our discussion of tangential velocity and other factors within the context of our pulley-belt assembly.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Tangential Velocity Dangers

Belt Velocity

Monday, August 21st, 2017

   Last time we developed an equation to compute tangential velocity, V, of the belt in our example pulley and belt system.   Today we’ll plug numbers into this equation and arrive at a numerical value for this belt velocity.

Belt Velocity

Belt Velocity

   

   The equation we’ll be working with is,

V = π × D2 ÷  t2                                                        (1)

where, D2 is the diameter of Pulley 2 and π represents the constant 3.1416. We learned that Pulley 2’s period of revolution, t2, is related to its rotational speed, N2, which represents the time it takes for it to make one revolution and is represented by this equation,

N2 = 1 ÷ t2                                                                            (2)

   We’ll now solve for the belt’s velocity, V, using known values, starting off with rearranging terms so we can solve for t2,

t2 = 1 ÷ N2                                                                           (3)

   We were previously given that N2 is 300 RPM, or revolutions per minute, so equation (3) becomes,

t2 = 1 ÷ 300 RPM = 0.0033 minutes                         (4)

   This tells us that Pulley 2 takes 0.0033 minutes to make one revolution in our pulley-belt assembly.

   Pulley 2’s diameter, D2, was previously determined to be 0.25 feet.    Inserting this value equation (1) becomes,

 V = π × (0.25 feet) ÷ (0.0033 minutes)                  (5)

 V = 237.99 feet/minute                                         (6)

 

   We’ve now determined that the belt in our pulley-belt assembly zips around at a velocity of 237.99 feet per minute.

   Next time we’ll apply this value to equation (6) and determine the belt’s tight side tension, T1.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Belt Velocity

Tangential Velocity

Monday, August 14th, 2017

   Last time we introduced the Mechanical Power Formula, which is used to compute power in pulley-belt assemblies, and we got as far as introducing the term tangential velocity, V, a key variable within the Formula.   Today we’ll devise a new formula to compute this tangential velocity.

   Our starting point is the formula introduced last week to compute the amount of power, P, in our pulley-belt example is, again,

P = (T1 – T2) × V                                         (1)

   We already know that P is equal to 4 horsepower, we have yet to determine the belt’s tight side tension, T1, and loose side tension, T2, and of course V, the formula for which we’ll develop today.

   

Tangential Velocity

Tangential Velocity

   

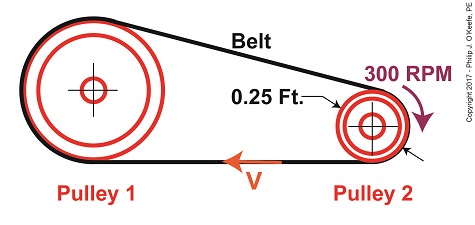
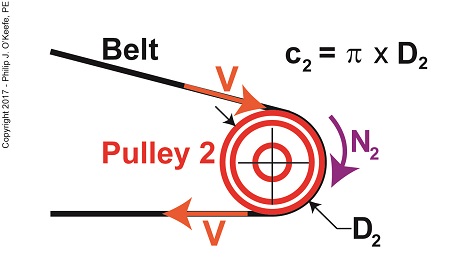
   Tangential velocity is dependent on both the circumference, c2, and rotational speed, N2, of Pulley 2.  The circumference represents the length of Pulley 2’s curved surface.   The belt travels part of this distance as it makes its way from Pulley 2 back to Pulley 1. The rotational speed, N2, represents the rate that it takes for Pulley 2’s curved surface to make one revolution while propelling the belt.   This time period is known as the period of revolution, t2, and is related to N2 by this equation,

N2 = 1 ÷ t2                                                                         (2)

   The rotational speed of Pulley 2 is specified in our example as 300 RPMs, or revolutions per minute, and we’ll denote that speed as N2 in light of the fact it’s referring to speed present at the location of Pulley 2.   As we build the formula, we’ll be converting N2 into velocity, specifically tangential velocity, V, which is the velocity at which the belt operates, this in turn will enable us to solve equation (1).

   Why speak in terms of tangential velocity rather than plain old ordinary velocity?  Because the moving belt’s orientation to the surface of the pulley lies at a tangent in relation to the pulley’s circumference, c2, as shown in the above illustration.   Put another way, the belt enters and leaves the curved surface of the pulley in a straight line.

   Generally speaking, velocity is distance traveled over a period of time, and tangential velocity is no different.  So taking time into account we arrive at this formula,

V = c2 ÷ t2                                                                          (3)

   Since the surface of Pulley 2 is a circle, its circumference can be computed using a formula developed thousands of years ago by the Greek engineer and mathematician Archimedes.   It is,

c2 = π × D2                                                            (4)

where D2 is the diameter of the pulley and π represents the constant 3.1416.

   We now arrive at the formula for tangential velocity by combining equations (3) and (4),

V = π × D2 ÷ t2                                                    (5)

   Next time we’ll plug numbers into equation (5) and solve for V.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Tangential Velocity

Mechanical Power Transmission – The Centrifugal Clutch in Operation

Sunday, April 22nd, 2012
     Just the other day I unexpectedly experienced the effects of centrifugal force while  driving home from the grocery store.  The checker had packed my entire order into one bag, making it top heavy.  Then en route someone cut me off at an intersection, and I had to make a sharp turn to avoid a crash.  During this maneuver centrifugal force came into play, forcing my grocery bag out of its centered position on the front seat next to me.  It lurched into the passenger’s door, fell over, and spilled its contents onto the floor.  Fortunately the eggs didn’t get smashed.

     In previous articles we identified the component parts of a centrifugal clutch mechanism and learned how centrifugal force makes objects spinning in a circular path about a fixed point move outward.  We can now explore what happens when we couple a centrifugal clutch mechanism to the engine of a grass trimmer.

     Figure 1 depicts the spinning clutch mechanism of a gas engine when it’s just been started and is operating at a slow idle speed.

centrifugal clutch mechanism

Figure 1

 

     Like the red ball in my previous article on centrifugal force, the blue centrifugal clutch shoes each have a mass m.  They spin around a fixed point P, situated at the center of the yellow engine shaft coupling.  Point P is located a distance r from the center of each shoe.  The shoes in motion have a tangential velocity V, and in accordance with Sir Isaac Newton’s Law of Centrifugal Force, the force Fc acts upon each shoe, causing them to want to pull out from the center of the mechanism, away from the fixed point.  Since idle speed is rather slow, however, the centrifugal force exerted upon the shoes isn’t strong enough to overcome the tension of the two springs and the coils connecting them remain coiled, holding the shoes tightly in position on the green boss.

     So what happens when we press the throttle trigger on the gas engine and cause the engine to speed up?  See Figure 2.

clutch shoes

Figure 2

 

     Figure 2 shows the clutch mechanism spinning at an increased velocity.  The tangential velocity V increases, and according to Newton’s law, the centrifugal force Fc acting on the clutch shoes increases as well.  The force is so strong that it overcomes the tension in the springs and they extend.  The clutch shoes are caused to move out and away from fixed point P, as well as from each other, traveling along the ends of the boss.

     When we remove our finger from the throttle trigger, the engine will slow down and return to idle speed.  The centrifugal force will decrease and the springs will pull the shoes back towards fixed point P.  The mechanism will return to its previous state, as shown in Figure 1.

     Next time we’ll insert the centrifugal clutch mechanism into the clutch housing to see how mechanical power is transmitted from the engine to the cutter head in our grass trimmer.

____________________________________________

 

Tags: , , , , , , , , , , , , , , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Mechanical Power Transmission – The Centrifugal Clutch in Operation

Mechanical Power Transmission – Centrifugal Force and Centrifugal Clutches

Monday, April 9th, 2012
     I’m not a big fan of amusement parks.  The first time I rode on a Tilt-A-Whirl I was caught off guard and flung onto my side by the centrifugal force acting upon my body, the lower half of which was constrained by a seat belt so I wouldn’t be catapulted out during the ride.  To make matters worse, the centrifugal force started to force the lunch I’d made the mistake of eating just before back up my throat.  It was a very unpleasant experience to say the least.

     Centrifugal force is an interesting phenomenon, and its principles are involved in the operation of a centrifugal clutch, which we’ll see later.  For now, let’s get a basic understanding of what it’s all about, thanks to the discoveries of Sir Isaac Newton in the late 17th Century.

 Centrifugal Force

Figure 1

 

     Figure 1 shows a red ball, whose mass we’ll notate m, attached to a string, the other end of which is attached to a fixed point, such as if you held it taught between your fingers.  If you’re in a playful mood, you might enjoy twirling the ball above your head on its string.  The distance between the center of the ball and the fixed point is labeled r, which stands for the radius of the circular path traveled by the ball as it twirls around the fixed point.   The speed at which the ball travels through the air is called its straight line velocity, or tangential velocity in scientific-speak, and it is generally notated as a V.  The centrifugal force, or Fc, that is exerted upon the ball as it whirls around your head is, Sir Isaac tells us, measured by the equation:

Fc = mV2/r

     Centrifugal force in the simplest of terms is an outward-pushing force that pulls objects in motion away from the point about which they’re rotating.  Let’s hold as fact that if m and r don’t change, then Newton’s equation tells us that the centrifugal force exerted upon the object in motion increases by the square of the velocity, or speed, of the ball.  In other words, the faster the ball moves as you spin it around your head on the string, the harder the centrifugal force that acts upon it.  As you spin the ball faster and faster, it will pull outward more and more strenuously, exerting ever greater resistance upon the string you hold between your fingers.

     Now suppose we replace the string in this example with a spring as shown in Figure 2. 

centrifugal force clutch spring

Figure 2

 

     Why a spring?  Because that’s what’s used within a centrifugal clutch.  Just as with the string, the ball’s velocity increases as you increase rotation speed around the fixed point, and the centrifugal force acting upon its mass by the spinning action increases as well.  The spring expands, extending further and further out from its beginning position of attachment to the fixed point, your fingers.  As velocity decreases, the spring will retract, eventually returning to its original coil size.  This extending and retracting action is the major mechanism at play within a centrifugal clutch.

     Next time we’ll explore a centrifugal clutch mechanism in more depth to observe its behavior relative to its spring under the influence of centrifugal force.

____________________________________________

 

Tags: , , , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | 1 Comment »