|
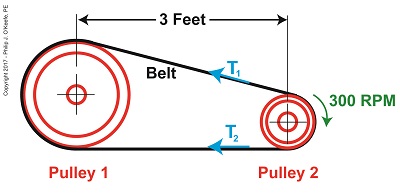
Last time we introduced a scenario involving a hydroponics plant powered by a gas engine and multiple pulleys. Connecting the pulleys is a flat leather belt. Today we’ll take a step further towards determining what width that belt needs to be to maximize power transmission efficiency. We’ll begin by revisiting the two T’s of the Euler-Eytelwein Formula and introducing a formula to determine a key variable, angle of wrap. The Angle of Wrap Formula
We must start by calculating T1, the tight side tension of the belt, which is the maximum tension the belt is subjected to. We can then calculate the width of the belt using the manufacturer’s specified safe working tension of 300 pounds per inch as a guide. But first we’ll need to calculate some key variables in the Euler-Eytelwein Formula, which is presented here again, T1 = T2× e(μθ) (1) We determined last time that the coefficient of friction, μ, between the two interfacing materials of the belt and pulley are, respectively, leather and cast iron, which results in a factor of 0.3. The other factor shown as a exponent of e is the angle of wrap, θ, and is calculated by the formula, θ = (180 – 2α) × (π ÷ 180) (2) You’ll note that this formula contains some unique terms of its own, one of which is familiar, namely π, the other, α, which is less familiar. The unnamed variable α is used as shorthand notation in equation (2), to make it shorter and more manageable. It has no particular significance other than the fact that it is equal to, α = sin-1((D1 – D2) ÷ 2x) (3) If we didn’t use this shorthand notation for α, equation (2) would be written as, θ = (180 – 2(sin-1((D1 – D2) ÷ 2x))) × (π ÷ 180) (3a) That’s a lot of parentheses! Next week we’ll get into some trigonometry when we discuss the diameters of the pulleys, which will allow us to solve for the angle of wrap.
Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Tags: angle of wrap, belt, belt tension, coefficient of friction, Euler-Eytelwein Formula, mechanical power transmission, pulley, pulleys