|
Edmund Halley was faced with a real puzzle when he began his quest to determine the distance of Earth from the sun. One of the pieces to solving that puzzle came from the work of a German mathematician, astronomer and astrologer named Johannes Kepler. Early in the 17th Century, Kepler spent a lot of time observing the planets in our solar system as they orbited the sun. He discovered that by taking note of the time it took for a planet to make one orbit around the sun, he could determine its relative distance from it. He then compared his findings with other planets, noting the time it took for each to make this same journey. His discovery would come to be known as Kepler’s Third Law of Planetary Motion. But what exactly is meant by a planet’s “relative distance from the sun”? In essence, it means that interplanetary distances, like just about everything else, are relative. Put another way, heavenly bodies can be said to be a distance X relative to another heavenly body if you establish a value for X, whether it’s numerical or otherwise. In Kepler’s case, X would be the unknown value of a so-called astronomical unit (AU), where one AU is equal to the unknown distance from Earth to the sun. Represented in equation form, this distance is: rEarth-sun = 1 AU This relative marker of distance could then be used to show how far the other planets are from the sun, relative to Earth’s distance from the sun, the AU. Kepler’s astronomical unit is simply a placeholder term for an unknown quantity, similar to any other unknown variable that might be used in an algebraic equation. For example, Kepler observed the orbits of Venus and Mars and determined their relative distances to the sun to be: rVenus-sun = 0.72 × 1 AU = 0.72 AU rMars-sun = 1.5 × 1 AU = 1.5 AU In other words, Venus’ distance from the sun is just under three quarters of Earth’s and Mars is one and a half times Earth’s distance from the sun. In this way, Kepler was able to determine the relative distances from the sun in AU for all the observable planets in our solar system. Kepler felt sure that one day scientists would be able to accurately measure Earth’s distance from the sun, and when they accomplished this they could employ his astronomical unit system to determine distances between other planets in our solar system and the sun. Next time we’ll introduce the principle of parallax and see how Halley used this optical effect to devise a method for assigning a value to Kepler’s unknown AU. ____________________________________ |
Archive for December, 2014
Kepler’s Third Law Of Planetary Motion
Wednesday, December 31st, 2014How Far Away is the Sun?
Wednesday, December 24th, 2014|
Astronomers tell us that the sun is approximately 93,000,000 miles from Earth. Since no direct method of measuring this distance exists, how did scientists determine this? They had to resort to indirect methods. In the early 18th Century, British astronomer, mathematician and physicist Edmund Halley, of Halley’s Comet fame, devised a method to measure the distance between Earth and its sun with reasonable accuracy. His method was based in part on an optical effect known as the principle of parallax, which had been discovered more than 2000 years ago by Greek astronomer Hipparchus when he also employed it to try and determine that same distance. Halley also employed the ideas of 17th Century German mathematician, astronomer, and astrologist Johannes Kepler. Kepler’s work on planetary motion, in particular the geometry of planetary orbits in our solar system, were vital to Halley’s distance measuring method. Next time we’ll see how Kepler’s Third Law of Planetary Motion brought Halley one step closer to methodology that would determine the distance of our home planet to its sun. _______________________________________
|
Thanks For the Gift, Sir Isaac
Friday, December 19th, 2014|
It’s the season of giving. The time of year we’re most apt to remember our loved ones and those who provide service to us by bestowing them with gifts. It’s a time when traditions and nostalgia for things past may cause us to get emotional. We celebrate many holidays throughout the year, memorializing veterans, family members, political leaders, but none to celebrate the scientist, the inventor, those individuals who have graced mankind with their insights, courage, and perseverance to go beyond the ordinary, to dare to understand things most would believe are beyond human understanding. The accomplishments of these uncelebrated figures have elevated humanity time and again. Where are their days? The scientist in me would like to see a Sir Isaac Newton Day, an Albert Einstein Day, Madame Curie Day, Stephen Hawking Day — Americans could use more days off to relax. And when the youngsters in our charge ask, “Who’s Einstein? Who’s Madame Curie?”, we could regale them with tales of the heroes that contributed to our understanding of the workings of the universe. Perhaps the information might prove inspirational enough to the receptive young mind to light the fire of exploration within them. Scientists throughout history have given us many gifts, the type of gifts that change things forever. They may not be what first comes to mind when imagining heroes, but in my mind they’re nothing less. Wishing you all an inspirational and happy holiday season and New Year! _______________________________________
|
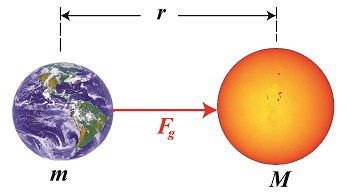
Gravity and the Mass of the Sun
Friday, December 12th, 2014|
As a young school boy I found it hard to believe that scientists were able to compute the mass of our sun. After all, a galactic-sized measuring device does not exist. But where there’s a will, there’s a way, and by the 18th Century scientists had it all figured out, thanks to the work of others before them. Newton’s two formulas concerning gravity were key to later scientific discoveries, and we’ll be working with them again today to derive a third formula, bringing us a step closer to determining our sun’s mass. Newton’s Second Law of Motion allows us to compute the force of gravity, Fg, acting upon the Earth, which has a mass of m. It is, Fg = m × g (1) Newton’s Universal Law of Gravitation allows us to solve for g, the sun’s acceleration of gravity value, g = (G × M) ÷ r2 (2) where, M is the mass of the sun, r is the distance between the sun and Earth, and G is the universal gravitational constant. You will note that g is a common factor between the two equations, and we’ll use that fact to combine them. We’ll do so by substituting the right side of equation (2) for the g in equation (1) to get, Fg = m × [(G × M) ÷ r2] then, using algebra to rearrange terms, we’ll set up the combined equation to solve for M, the sun’s mass: M = (Fg × r2) ÷ (m × G) (3) At this point in the process we know some values for factors in equation (3), but not others. Thanks to Henry Cavendish’s work we know the value of m, the Earth’s mass, and G, the universal gravitational constant. What we don’t yet know is Earth’s distance to the sun, r, and the gravitational attractive force, Fg, that exists between them. Next time we’ll introduce some key scientists whose work contributed to a method for computing the distance of our planet Earth to its sun. _______________________________________
|
The Inverse Relationship of the Acceleration of Gravity
Friday, December 5th, 2014|
In this blog series we’ve been working our way towards determining mass values for heavenly bodies in our universe. Today we’ll explore the inverse relationship phenomenon that’s present when examining the acceleration of gravity between two heavenly bodies, for our purposes Earth and its moon. To demonstrate the inverse relationship phenomenon, we’ll use Newton’s Law of Gravitation formula: g = (G × M) ÷ r2 (1) In this formula g represents Earth’s acceleration of gravity that’s acting upon the moon. The center of the moon is located at a distance r from Earth’s center. Earth’s mass is represented by M, and G is the universal gravitational constant, which never varies from its value of 3.49 × 10-8 cubic feet per slug per second squared. We’ll solve for Earth’s g factor relative to the moon, which we’ll position at varying distances from Earth’s core, thereby demonstrating how the attracting force of Earth’s gravity becomes weaker as the moon’s distance from Earth’s core increases — hence the inverse relationship. To begin, we know that the present distance from Earth’s center to the center of the moon is about 238,900 miles, or 1,261,392,000 feet. We also know that Earth’s mass, M, is equal to 4.09 × 1023 slugs. Plugging these values into Newton’s Law of Gravitation equation, we calculate the acceleration of gravity exerted upon the moon in this, its normal orbit, to be: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (1,261,392,000 ft)2 g = 0.0089 ft/sec2 Now let’s suppose that the moon’s orbit was caused to increase so that it became situated 400,000 miles, or 2,112,000,000 feet from Earth. Earth’s acceleration of gravity exerted upon the moon at this distance would be calculated as: g = ((3.49 × 10-8 ft3/slug/sec2) × (4.09 × 1023 slugs)) ÷ (2,112,000,000 ft)2 g = 0.0032 ft/sec2 From these two examples we can see that the further the moon is positioned from Earth, the weaker Earth’s gravitational pull upon it is. This gravitational pull is the force of gravity, Fg, introduced in our last blog, a term which originates in Newton’s Second Law of Motion, as given by the equation: Fg = m × g (2) where, in this case, m represents the mass of the moon. Next time we’ll combine equations (1) and (2) and derive a third formula which will allow us to calculate the mass of the sun.
_______________________________________
|