|
Last time we began our discussion on velocity by focusing on one of its aspects, distance, and we calculated Earth’s orbital distance around the sun to be 5,816,023,200 miles. Today we’ll focus on velocity’s other aspect, time. Together, these aspects will allow us to solve for Earth’s orbital velocity, aka speed. When early astronomers monitored Earth’s journeys, they found it took exactly one year for it to complete its orbit around the sun. They combined this fact with Earth’s orbital travel distance of 5,816,023,200, or 9.36 × 1011 meters — meters being the unit of measurement most often used in scientific computations — and solved for Earth’s orbital velocity as follows, v = 9.36 × 1011 meters ÷ 1 year = 9.36 × 1011 meters per year The scientific notation of 9.36 × 1011 equates to 936,000,000,000 meters, a large and unruly number to work with. We can simplify things further by breaking this number down into units of meters per second, which will then allow us to arrive at Earth’s velocity in terms of miles per hour, something most Earthlings can relate to. One meter per second is equal to 2.237 miles per hour, and there are 31,536,000 seconds in one year, so breaking Earth’s orbital velocity down into meters per second we arrive at, v = 9.36 × 1011 meters ÷ 31,536,000 seconds = 29,680 meters per second v = (29,680 meters per second) × (2.237 mph/m/sec) = 66,394 miles per hour Yes, it’s true, Earth whips around the sun at warp speed. Our fastest man made rockets only achieve speeds of about 25,000 miles per hour. Earth beats them two-to-one! Now that we know Earth’s orbital velocity, we have everything we need to calculate the gravitational force exerted on Earth by the sun. We’ll do that next time.
____________________________________
|
Archive for July, 2015
Earth’s High Speed Race Around the Sun
Tuesday, July 28th, 2015Earth’s Orbital Velocity
Sunday, July 19th, 2015|
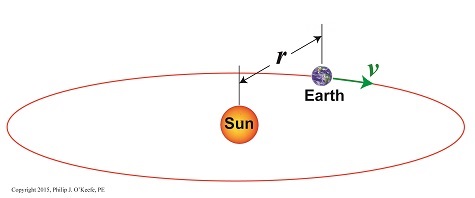
Last time we introduced Newton’s equation to calculate the sun’s gravitational force acting upon Earth, and today we’ll begin solving for the last remaining unsolved variable within that equation, v, Earth’s orbital velocity. Here again is Newton’s equation, Fg = [m × v2] ÷ r For a refresher on how we solved for m, Earth’s mass, and r, the distance between Earth and the sun, follow these links to past blogs in this series, What is Earth’s Mass and Calculating the Distance to the Sun. Velocity, or speed, as it’s most commonly referred to, is based on both time and distance. To bear this out we’ll use an object and situation familiar to all of us, traveling in a car. The car’s velocity is a factor of both the distance traveled and the time it takes to get there. A car traveling at a velocity of 30 miles per hour will cover a distance of 30 miles in one hour’s time. This relationship is borne out by the formula, vCar = distance traveled ÷ travel time vCar = 30 miles ÷ 1 hour = 30 miles per hour Similarly, v is the distance Earth travels during its orbital journey around the sun within a specified period of time. It had been observed since ancient times that it takes Earth one year to complete one orbit, so all that remained to be done was calculate the distance Earth traveled during that time. Vital to calculations was the fact that Earth’s orbit is a circle, which allows geometry to be employed and calculations to be thereby simplified. Refer to Figure l. Figure 1 From geometry we know that the circumference of a circle, C, is calculated by, C = 2× π × r where π is a constant, the well known mathematical term pi, which is equal to 3.1416, and r is the radius of Earth’s circular orbit, determined, courtesy of the work of Johannes Kepler and Edmund Halley, to be approximately 93,000,000 miles. Stated in metric units, the unit of measurement most often employed in science, that comes to 149,000,000,000 meters. Inserting these numerical values for π and r into the circumference formula, scientists calculated the distance Earth travels in one orbit around the sun to be, C = 2 × π × 149,000,000,000 meters = 9.36 x 1011 meters Next time we’ll introduce the time element into our equations and solve for v, and from there we’ll go on and finally solve for Fg, the sun’s gravitational force acting upon Earth.
____________________________________
|
Centripetal Force Makes the Earth Go Round
Thursday, July 9th, 2015|
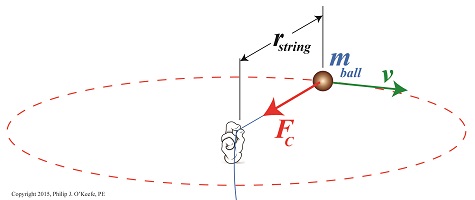
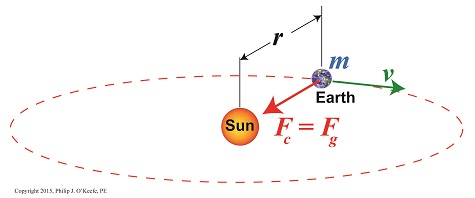
Last time we saw how centripetal force is responsible for keeping a child’s ball moving in a circular path when twirled above his head. Today we’ll see how that same force is responsible for keeping Earth in its rotation around the sun. We’ll use Isaac Newton’s Second Law of Motion as it relates to centripetal force to bear that out today. Our example from last week, Figure 1 According to Newton’s Second Law of Motion, Fc, the centripetal force acting upon the ball, is calculated by the equation, Fc = [mball × v2] ÷ rstring where, mball is the ball’s mass, v the ball’s velocity, and rstring is the length of the string. The mechanics are obviously different with regard to Earth and its orbit around the sun, where there’s no obvious physical link between the objects in rotation. In this case the sun’s gravitational force, Fg, acts to tether Earth to it. And just like the string and ball, the sun’s gravitational tether creates a centripetal force, Fc, which prevents Earth from leaving its orbital path. See Figure 2. Figure 2 Newton concluded that for the Earth to remain on its permanent, fixed path of orbit around the sun, Fc must be equal to Fg, and that the forces in play between the sun and Earth were like a gigantic tug of war where neither side is able to pull any harder than the other. This stalemate is responsible for keeping Earth stably in place in its orbit. According to Newton’s Second Law, the sun’s gravitational force acting upon the Earth is calculated by, Fg = Fc = [m × v2] ÷ r where, m is Earth’s mass, v its orbital velocity, and r the distance between Earth and the sun. Thanks to early scientists like Edmund Halley and Henry Cavendish, the values for m and r had already been determined. That left v, Earth’s orbital velocity, the only variable remaining to be solved. We’ll see how 19th Century scientists accomplished that next time.
____________________________________
|
Centripetal Force
Friday, July 3rd, 2015|
Have you ever wondered how Earth keeps its steady orbit around its life sustaining sun, or what prevents it from breaking away and flying off willy-nilly into the universe? It’s more than just simple gravity, it’s the physics behind centripetal force, the topic we’ll be exploring today. We’ve been working our way towards a full discussion on gravity in this long blog series, navigating subjects such as the behavior of falling objects, the acceleration of gravity, the masses of Earth and the sun, and the optical measurement of cosmic distances. We’ve now come full circle from my opening blog on the subject, Gravity and the Mass of the Sun. In that blog an equation was introduced as a means to calculate the mass of the sun, and in that equation is the variable we’ll be working towards solving today, Fg, the sun’s gravitational force upon the Earth. Here again is that equation, M = (Fg × r2) ÷ (m × G) Gravity, mass, and distance all come into play in forming the structure of our universe, and the variables in this equation reflect that: M, the mass of the sun, r the distance between Earth and the sun, m the Earth’s mass, and G the universal gravitational constant. With the exception of Fg, all variables in this equation have already been solved for in previous blogs in this series. For a refresher go to, Calculating the Distance to the Sun, What is Earth’s Mass? and Newton’s Law of Gravitation and the Universal Gravitational Constant. As there is no direct means to measure the cosmic quantity, Fg, we’re left to an indirect method for its computation. The indirect method is based on the phenomenon of centripetal force, Fc something most children become acquainted with when they experience the thrill of twirling an object attached to a string, say a rubber ball, above their heads. See Figure 1. Figure 1 As the ball is twirled, the string becomes taut. The energy exerted upon it by the child’s hand, coupled with the ball’s mass and traveling speed/velocity, v, make the ball want to move off in a straight trajectory into space, like a launched projectile. But the string it’s attached to prevents it from doing so, forcing the ball to instead travel a circular path around the center point of rotation. The taut string and the ball’s circular path are evidence of centripetal force, Fc, at work. Next time we’ll employ Isaac Newton’s Second Law of Motion to the centripetal force phenomenon to see how the sun’s gravitational force keeps Earth in a stable circular orbit around the sun.
____________________________________
|