|
Metals, polymers, ceramics, and composites… Oh, my! Imagine Dorothy, lost in a forest of these materials while on her way to Oz. The Scarecrow is most probably a composite being. And the Tin Man is most definitely made of metal. But that Cowardly Lion sure poses a quandary for Dorothy. Is this beast polymer, ceramic, or something else? She soon learns that he’s comprised of organic materials, and that’s in a whole different forest. What’s he doing here, anyway? The Tin Man was strong enough to cut down trees, until he got rained on. As you’ve probably noticed, metallic materials such as steel are the most frequently used to make machine and structural components, and this is primarily due to their strength and durability. As a result of the frequency of their usage, the formation of metal materials and their resulting properties are the primary focus of material science study for mechanical engineers. To prevent our Tin Man from rusting after the rain, he should have been formulated with particular properties which provide not only strength but corrosion resistance. The main ingredient in the recipe for his fancy silver garb would then be iron. You would add carbon and other elements in specific proportions to the iron under carefully controlled heating conditions in a blast furnace. You would then cool the molten steel down at a controlled rate and subject it to mechanical forces after it is solidified. Voila! The material is ready to be cut and shaped into components, and our Tin Man would be all set, prepared to withstand the onslaught of any weather. The study of the formation and properties of polymers and ceramics is also an important part of materials science study. Polymers, often used to make plastics, consist of large molecules which comprise non-metallic elements like carbon, hydrogen, and oxygen. Now those are materials that organic beings are also made of. Could it be that our Cowardly Lion was a polymer? Ceramics are hard and brittle materials consisting of both metallic and nonmetallic elements. There are many examples of ceramic materials ranging from cements to cutting bits for machine tools. Cowardly Lion could not possibly be made of these; he is anything but hard and brittle. Then there is a whole world of very unique things, like our Scarecrow, that are made of composite materials. Sure, he’s made of straw, and he’d be the first one to admit to that, but what about that dashing outfit of his? Composite materials consist of two or more materials combined to make a material with properties distinctly different from the original constituent materials by themselves. An example composite material that might have worked better for Scarecrow is fiberglass, where glass fibers are mixed with polymer resins. Glass by itself is brittle and easily broken, but when it is formed into thin fibers and combined with polymer resin, then allowed to harden and cure, the composite material becomes strong and durable. The fiberglass can then be easily shaped into forms to make automobile bodies, boat hulls… and scarecrow parts? At least it’s not highly flammable, like Scarecrow’s straw. Other examples of composites include steel reinforced concrete, Kevlar, plywood, safety glass, and carbon reinforced plastic. Most of these would have worked better for our Scarecrow than what he was originally endowed with. Well, that’s materials science in a nutshell. We’ll discuss thermodynamics next time, which is the study of the properties of steam and other media used to absorb and transfer heat energy in power plants, engines, and refrigeration systems. Hmm, I wonder if the Wicked Witch had the inside track on this stuff? _________________________________________________________________ |
Archive for November, 2009
Materials Science In Mechanical Engineering, Part I
Sunday, November 22nd, 2009|
Imagine a chef without a fry pan, a mixer, or attempting to create a recipe without any idea of how the ingredients will combine. Is the end result likely to be something you’d want to eat? Something with just the right visual appeal, aroma, taste, and texture? Unlikely. Likewise, what good would a mechanical design be if an engineer had no idea of what kind of materials to use? The results would be haphazard, and this could lead to problems more serious than lack of palatability. We’re talking serious consequences here, such as product failure, injury, or death. In the mechanical engineering arena, just as in the cooking arena, materials used possess certain properties which render them useful for specific purposes. Just as a chef has her pantry, an engineer has a wide variety of materials available to her to choose from, and new materials are developed all the time. The vastness of the materials available to an engineer makes it difficult for all of them and their properties to be committed to memory. What is possible, however, is to develop a firm understanding of the underlying principles that govern their properties. It is this general understanding of materials’ properties that enables engineers to select between materials. There are key questions to be answered in the search for the ideal materials to do a job. Which materials would be the most economical? Which would give optimal performance? The best durability? Materials science provides an understanding of the relationship between the structure of materials at an atomic or molecular level and their macroscopic properties. In other words, the engineer learns how atoms are arranged and bonded together at a microscopic level, which in turn form the material perceived by the naked eye. The ultimate arrangement of molecules is based upon how the virgin material was processed into its final form. By “processed,” I mean the application of heat, cooling, mechanical forces, etc. Knowing the composition of a material and how it was processed allows engineers to predict how the material will react to things like stress, strain, heat, corrosives, radiation, and electrical currents. It’s a big world out there, and it’s filled with materials to explore. Next week we’ll begin that exploration. _________________________________________________________________ |
Strengths of Materials in Mechanical Engineering
Sunday, November 15th, 2009|
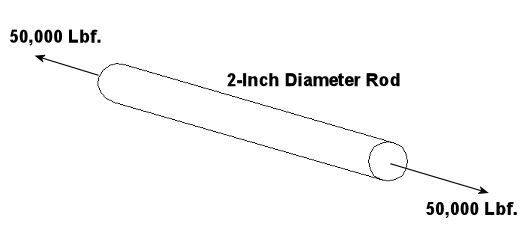
When we looked at our statics example a few posts ago, it was convenient to consider the bridge beam as being perfectly rigid. In the real world, a bridge beam is not perfectly rigid. When it’s subjected to external forces, like the weight of a truck sitting in the middle of it, there is a tendency for it to bend, deform, change its shape. If the external forces create bending and deformations that are too much for the bridge beam material to handle, it will collapse. In strengths of materials analysis, engineers must consider typical stresses that will occur within objects like bridge beams, airplane wings, bolts, and machine parts during use. Stress is a measure of force exerted per unit area of a surface. Once the stresses are known, a material is selected that is strong enough to keep the object from being bent, mashed, stretched, and/or broken. To illustrate this, let’s consider an example of a simple stress. Suppose you want to design a truss rod for a highway bridge like the one shown in Figure 1. Specifications require that the rod be two inches in diameter. Its purpose is to hold the sides of the bridge together when vehicles travel across it. Figure 1 Now suppose that the bridge is to handle traffic to and from and iron mine. Let’s consider the scenario where a truck laden with iron ore runs out of gas and comes to a stop in the middle of our bridge. Under this load, static analysis reveals that the sides of the bridge want to spread apart, putting a tension of 50,000 pounds force (Lbf.) on the truss rod as shown in Figure 2. Figure 2 Since the external force acting upon the truss rod and the diameter of the rod itself are both given, the engineer would merely have to select the appropriate material for the rod that would fall within the desired parameters, that is, so as to keep our rod from pulling apart when anticipated stressors such as a heavy truck is on the bridge. The first step would be to calculate the tensile stress within the rod itself. By tensile stress, I mean the stress in the rod due to the forces that are trying to pull it apart. In our example, this is relatively easy to assess: Stress = [Tensile Force] ÷ [Lateral Cross Sectional Area of the Rod] The lateral cross section of the rod is round, so its area would be πd2 divided by 4, where the Greek letter π (Pi) has a value of 3.1416, and d is the diameter of the rod. Therefore, the tensile stress would be: Stress = [50,000 Lbf.] ÷ [π × (2 in.)2 ÷ 4] = 15,915.49 Lbf./in.2 Knowing the stress within the rod, the engineer would next have to select an appropriate material for the rod that’s strong enough to do the job. In our case, let’s say we determine that steel is the best material to use. But what type of steel? Well, there are engineering handbooks with tables that list the mechanical properties of all sorts of materials, including metals and plastics, and along with those properties there is listed their ability to handle stress. These mechanical properties were determined in laboratory tests where carefully machined specimens of the materials were subjected to measured stresses until they deformed and broke apart. They include yield strength and ultimate strength, and these findings have been duly recorded so that future engineers need not go through independent testing of common materials themselves. Yield strength is the stress that is measured when the test specimen begins to stretch without any significant increase in force being applied to it. Ultimate strength is the maximum stress that the material in the test specimen can withstand before it starts to fail, that is tear apart, break, collapse. Our engineer would use the mechanical properties tables that are readily available to him to select the appropriate steel alloy that would meet our criteria, that is, has a listed strength high enough above the calculated 15,915.49 Lbf./in.2 tensile stress to provide a sufficient factor of safety. Factors of safety are listed in engineering books for yield strength and ultimate strength and they are selected depending on how the forces are applied to a structural component or machine part (e.g. steady, varying, or shock). When strengths of materials analysis involves the solution of complex statics and dynamics problems, things become a little less straightforward. And when you are dealing with components having odd shapes and a combination of stresses, say due to compression and torsion, things become even more complex. In any case, engineers must have extensive knowledge of the properties of materials in order to anticipate factors at play in real world scenarios such as the one we’ve been discussing. Ever wonder why some steel is hard and brittle, and some is soft and bendable? Well, our next topic of discussion will be about materials science, the study of how metal alloys and polymers are formed to have specific properties. _________________________________________________________________ |
Kinematics of Machines in Mechanical Engineering
Sunday, November 8th, 2009|
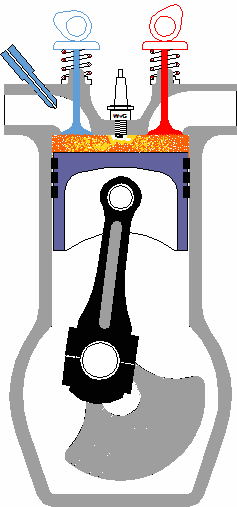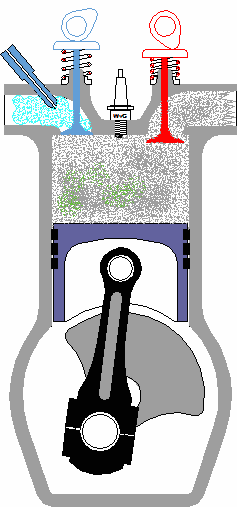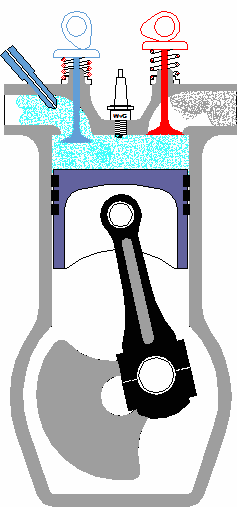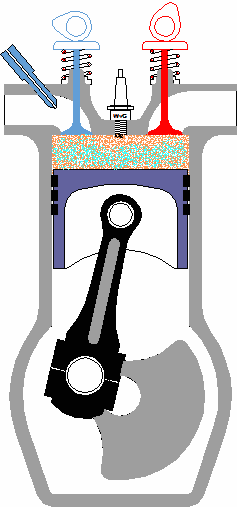
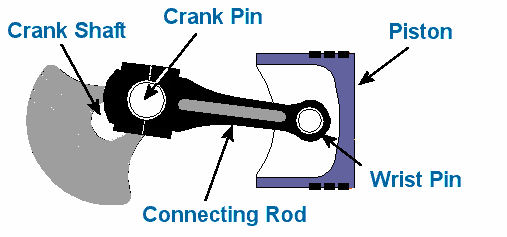
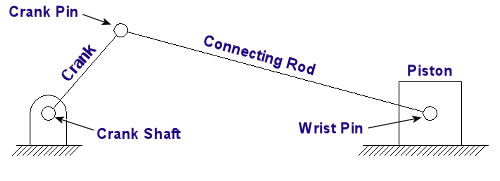
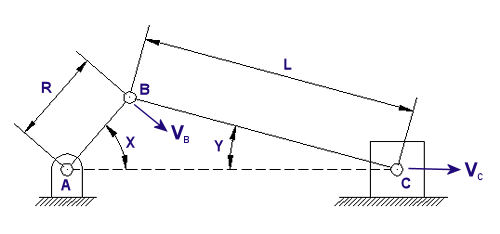
When we refer to the study of the kinematics of machines, we’re referring to the relationship between machine parts and how those parts behave as they move through their ranges of motion. What this means is that there is particular concern with the relative motion of machine parts, that is, how they relate to each other, their position, distance, velocity, and acceleration. When speaking of the kinematics of machines, a mechanism is considered to be like a chain with a system of links that are connected together. This chain is constrained, meaning that independent movement of one part is not possible. These parts are interconnected, and they all move relative to each other. Motion in any one link of this kinematic chain will result in a relative and predictable motion to each of the others. Now, by “chain,” I don’t necessarily mean a chain in the physical sense, but rather the fact that the parts of the mechanism are linked together. To illustrate what I’m talking about, let’s consider the gasoline engine shown in Figure 1 below. Figure 1 To help you follow along, let’s turn the engine on its side and name the parts of one of its kinematic chains. This is shown in Figure 2. Figure 2 Suppose you want to analyze how fast the engine’s piston is moving at any given instant during its operation. Suppose further that you know how fast the crank shaft is turning. Where would your analysis begin? Well, while studying the motions of machine parts, it’s helpful to draw the parts first in skeletal form so that only those dimensions that affect their motions are considered. Let’s represent the kinematic chain of Figure 2 in skeletal form. See Figure 3 Figure 3 Lastly, we embellish the skeleton with the depiction of angles that are at play as the parts of our engine move, and we add the relevant symbols that will allow us to build the equations we’ll be working with. This is shown in Figure 4. Figure 4 So, as the engine runs, the crank AB rotates around the center of the crank shaft A. The connecting rod BC is attached to the piston at the wrist pin C. The piston moves back and forth as AB rotates. Now here is where things get a little hairy, and for some of you it may look somewhat like code or a foreign language. The tangential velocity VB of the crank pin B is shown in Figure 4 as a vector. A vector is something which depicts both a magnitude and direction. And since VB is a “tangential velocity,” it is moving in a direction which is at a right angle, that is, at a 90-degree angle in relation to the crank AB. This relationship will always exist between VB and the crank AB. In the posed scenario, VB is a velocity, so let’s say its magnitude will be in units of inches per second. The magnitude of the vector VB is then directly related to the speed of crank shaft AB and is determined by this equation: VB = 2∏RN ÷ 60 Referring to Figure 4, R is the distance between the center of the crank shaft and the center of the crank pin in inches. N is the rotational speed of crank AB in revolutions per minute (rpm). If one knows the crank angle X, the crank length R, and the connecting rod length L in Figure 4, they can then use trigonometry to determine the velocity of the piston. This velocity is represented by the vector VC, and its magnitude, or value, would be found by using the following equation… VC = [VB] × [sin(X + Y)] ÷ [sin(90° – Y)] …where the angle Y is found by: Y = [sin-1(R ÷ L)] × [sin(X)] Analysis of kinematics of machines would become even more complicated when complex mechanisms like oddly shaped linkages, cams and followers, and gear trains are involved. Our next mechanical engineering topic will be: Strength of materials, the study of the properties of materials. Geometry and sizing of structural components, structures, and machine parts will also be explored. _________________________________________________________________ |
Mechanical Engineering, Focus on Dynamics, Part II, Kinetics
Monday, November 2nd, 2009|
In Part I of Mechanical Engineering, Focus On Dynamics, we talked about kinematics. This week in Part II, we’ll talk about kinetics. Kinetics is the study of the relationship that exists between forces acting on a body, the mass of the body itself, and its motion. It’s used to predict the motion caused by given forces acting on a body or to determine the forces required to produce a motion of the body. In kinetics forces can be attributed to the motion of an object by way of Sir Isaac Newton’s Second Law of Motion. In other words, this law relates the kinematics of an object to the forces applied to it, and in equation form that relationship looks like this: Force = [Mass] x [Acceleration] “Mass” is the weight of the object, in pounds, divided by the acceleration of the Earth’s gravity. On Earth, the acceleration of gravity is considered to be a constant and is taken to be 32.2 feet per second, per second. (No, that’s not a typo.) Legend has it that Newton discovered the earth’s acceleration when gravity caused an apple to fall from a tree and hit him on the head. That may or may not be true, but Newton’s Second Law of Motion forms the foundation for the study of kinetics. To illustrate how kinetics works, we can look at another very simple example. Suppose you have a block of steel that weighs 50 pounds, and it is sitting still on a nice smooth, frictionless sheet of ice (see Figure 1). Figure 1
How hard would you have to push on the side of this block to make it accelerate across the ice at a rate of 10 feet per second, per second? Use Newton’s second law to find out: Force = [(50 Lb.) ÷ (32.2 ft./second2)] x [10 ft./second2] Force = 15.5 Lb. Force and energy calculations in kinetics can get really complicated, especially when you have to consider the effects of friction, forces acting at angles, velocity, rotation, motion constraints, collisions, etc. Our next mechanical engineering topic will be: Kinematics of Machines, the study of how parts of machines behave as they move through their ranges of motion. _________________________________________________________________ |