|
Although I’m an engineering expert in the 21st Century, I often have to employ engineering principles that are centuries old. A case in point is Gaspard Gustave de Coriolis‘ formula to compute work, as set out in his Principle of Work. We’ll work with his formula today, and we’ll introduce a unit of measurement used to quantify work known as the Newton. de Coriolis’ formula to compute work is used to determine the amount of work, that is, the amount of dynamic energy available to influence the movement of an object, and is calculated by the formula, Work = Force × Distance where F represents the force acting upon an object that travels a distance of D. Force is most often expressed in metric units as kilogram • meter per second2, a wordy expression which is more conveniently referred to as the Newton. In the image below, F is the force of 178 Newtons exerted by the gardener to push his filled wheelbarrow a distance of 3 meters. The quantity 178 Newtons was obtained by way of direct personal experience working in my own garden. I’ve found that it takes approximately 40 pounds of force to push a wheelbarrow loaded with dirt across level ground. Because one pound of force is equal to 4.45 Newtons, the amount of force I exerted is expressed as, [40 pounds of force] × [4.45 Newtons per pound force] = 178 Newtons Work = Force × Distance If 178 Newtons of force is required to push the wheelbarrow a distance of 3 meters, then the work performed is expressed as, Work = 178 Newtons × 3 meters = 534 Newton • meters Next time we’ll explore the special relationship between work and energy and introduce another unit used to quantify work. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Archive for November, 2015
de Coriolis’ Formula to Compute Work and the Newton
Sunday, November 29th, 2015de Coriolis’ Principle of Work and Dynamode
Sunday, November 15th, 2015|
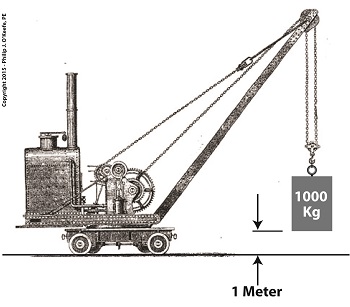
I was recently retained as an engineering expert in a lawsuit in which I had to determine the force acting upon an object. In order to quantify that force, I employed Gaspard Gustave de Coriolis‘ Principle of Work, an engineering concept he introduced in his 1829 textbook, Calculation of the Effects of Machines. We’ll take our first look at de Coriolis’ Principle of Work today, along with the term he used to quantify work, the dynamode. As a scientist living during the time of the great Industrial Revolution, de Coriolis was interested in lots of things, and he was particularly interested in quantifying the effort involved to accomplish tasks, like how many men, horses, or steam engines were required to move a stationary object. He defined this activity as work, and he hoped its study would lead to a broadly accepted engineering principle which could be applied across industrial functions. According to de Coriolis, work is the force acting upon a stationary object which causes it to move, multiplied by the distance moved. Work could also be defined as the force acting upon an object already in motion, multiplied by the distance traveled before it comes to a stop. To quantify work, de Coriolis proposed the dynamode as its unit of measure, a term which derives from the Greek words dynamis, meaning power, and odos, meaning path. He went on to define one dynamode as the amount of work required to lift an object with a mass of 1,000 Kg, or kilograms, one meter above the ground.
de Coriolis’ Dynamode Quantity
Catchy as it may sound, the word dynamode is all but forgotten today. But de Coriolis’ Principle of Work and his formula to calculate work remain to the present day as fundamental concept in engineering. We’ll present that formula next time. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Converting Kinetic Energy to Electrical Energy
Tuesday, November 3rd, 2015|
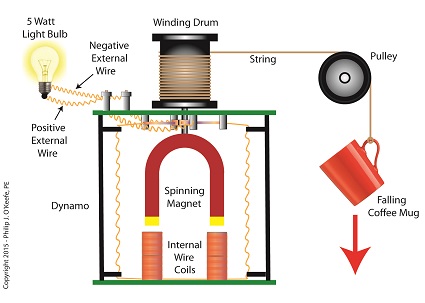
When acting as an engineering expert I’m often called upon to investigate incidents where energy converts from one form to another, a phenomenon that James Prescott Joule observed when he built his apparatus and performed his experiments with electricity. Today we’ll apply Joule’s findings to our own experiment with a coffee mug when we convert its kinetic energy into electrical energy and see how the units used to express that energy also change. We had previously calculated the kinetic energy contained within our falling coffee mug to be 4.9 kg • meter2/second2, also known as 4.9 Joules of energy, by using de Coriolis’ Kinetic Energy Formula. Now most of us don’t speak in terms of Joules of energy, but that’s easily addressed. As we learned in a previous blog on The Law of Conservation of Energy, all forms of energy are equivalent and energy can be converted from one form to another, and when it does, the unit of energy used to express it also changes. Let’s say we want to put our mug’s 4.9 Joules of kinetic energy to good use and power an electric light bulb. First we must first find a way of converting the mug’s kinetic energy into electrical energy. To do so, we’ll combine Joule’s apparatus with his dynamo, and connect the mug to this hybrid device with a string.
Converting Kinetic Energy to Electrical Energy As the mug falls its weight tugs on the string, causing the winding drum to rotate. When the drum rotates, the dynamo’s magnet spins, creating electrical energy. That’s right, all that’s required to produce electricity is a spinning magnet and coils of wire, as explained in my previous blog, Coal Power Plant Fundamentals – The Generator. Now we’ll connect a 5 Watt bulb to the dynamo’s external wires. The Watt is a unit of electrical energy named in honor of James Watt, a pioneer in the development of steam engines in the late 18th Century. Now it just so happens that 1 Watt of electricity is equal to 1 Joule of energy per a specified period of time, say a second. This relationship is expressed as Watt • second. Stated another way, 4.9 Joules converts to 4.9 Watt • seconds of electrical energy. Let’s see how long we can keep that 5 Watt bulb lit with this amount of energy. Mathematically this is expressed as, Lighting Time = (4.9 Watt • seconds) ÷ (5 Watts) = 0.98 seconds This means that if the mug’s kinetic energy was totally converted into electrical energy, it would provide enough power to light a 5 Watt bulb for almost 1 second. Next time we’ll see what happens to the 4.9 Joules of kinetic energy in our coffee mug when it hits the floor and becomes yet another form of energy. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |