|
Last week we introduced the transit of Venus, a natural phenomenon taking place only every 243 years and how Edmund Halley theorized its use to determine Earth’s distance from the Sun. Halley, master astronomer, mathematician and intrepid world traveler that he was, would have given his all to see this happen, but alas he would not. Most reading these words will not be aware that Earth dwellers in the year 2012 were fortunate enough to see this incredible phenomenon taking place within their own lifetimes. In fact, NASA captured it on film. Here it is, in ultra high definition, for all to enjoy: We’ll continue our blog series next time when we’ll look further into Halley’s methodologies.
____________________________________
|
Archive for May, 2015
The Transit of Venus, Caught on Video
Thursday, May 28th, 2015The Transit of Venus
Monday, May 18th, 2015|
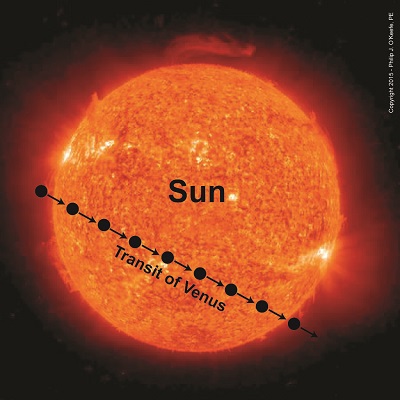
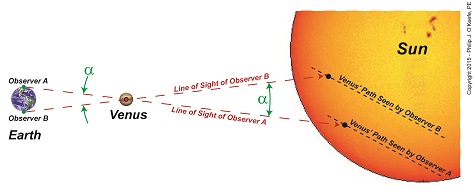
Last time we learned of Johannes Kepler’s Third Law of Planetary Motion and his development of the astronomical unit (AU) and how these contributed to bringing ancient scientists a step closer to calculating Earth’s distance to the sun. Today we’ll see why Kepler’s focus on Venus, specifically its travel through space in relation to Earth and the sun — the so-called transit of Venus — would become the crucial element to solving the puzzle. Astronomers had previously used the Earth itself as an optical rangefinder to calculate distance to the moon. But unlike the moon which is relatively close to Earth, the sun is many tens of millions of miles away, too distant to be used in that manner. When it came to finding the distance from Earth to its sun, they were stumped. Then in 1716 Edmund Halley had the insight to combine Kepler’s Third Law and the parallax principle with Venus’ orbital journeys to devise an ingenious solution to the problem. The transit of Venus, first predicted by Kepler in 1627, is a rare astronomical phenomenon which only occurs every 243 years. At this time Venus becomes clearly visible from Earth and appears as a black dot traveling a straight path across the fiery backdrop of the sun’s surface. Figure 1 shows this phenomenon as it would look from Earth. According to Halley’s plan, two observers with telescopes would be positioned on opposite sides of the Earth. Due to the principle of parallax their lines of sight would provide different perspectives of Venus’ path. See Figure 2. From the perspective of Observer B, Venus’s path would appear higher on the sun’s face than the path seen from the perspective of Observer A. As their lines of sight converge on Venus’ center, an angle forms between them, which we’ll name α. The same angle forms as they look past Venus to the sun in its backdrop. Halley theorized that if the angle α could be measured, Kepler’s Third Law could be used together with trigonometry to calculate the distance between Earth and the sun, Kepler’s so-called AU. We’ll review Halley’s methodology next time.
____________________________________
|
The Astronomical Unit — It’s So Relative
Thursday, May 7th, 2015|
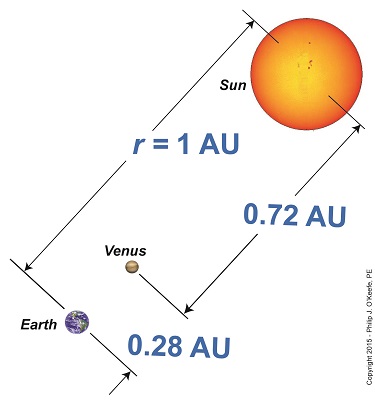
Last time we learned that early scientists used the Earth itself as an optical rangefinder to gauge its distance to the moon, and we posed the question: Can Earth be used in the same way to gauge distance to the sun? Unfortunately not. As we learned earlier in this blog series, the more distant the object, the larger the rangefinder that’s required, and the Earth just plain isn’t big enough to be used to compute that distance. The sun is 390 times farther away than the moon is, and that presents a real problem. Today we’ll learn about an alternate method to gauge this great distance. Johannes Kepler made a great contribution towards finding Earth’s distance to the sun when he developed his Third Law of Planetary Motion. Through his observation of planetary movements he was able to determine each planet’s relative distance from the sun in terms of what he dubbed the astronomical unit (AU), a yardstick by which the distance between all planets in our solar system and our shared sun could be judged. Kepler established the distance between Earth and the sun to be that astronomical unit, depicted in the illustration as r. The reason Kepler developed the AU was because in his day there was no known way to measure the distance to the sun. The AU, an abstract term with no real numerical value in terms of the distance being measured became a sort of placeholder term until r could actually be measured. The best the AU could do was allow him to determine how far a planet was from the sun relative to Earth’s distance from it. For example, his Third Law states that Venus’ distance to Earth is approximately one-quarter the distance between Earth and the sun, or 0.28 AU. That meant that Venus’ distance to the sun was three-quarters the distance of Earth to the sun, or 0.72 AU. Together, these two distances equaled one AU, the as yet unquantifiable distance r between Earth and the sun. Why all the fuss over Venus? Because Edmund Halley, a scientist who came after Kepler and shared in his fascination with interplanetary distances, would use Venus’ proximity to Earth to set up an optical rangefinder relationship between them and the object of his fixation, the sun. Crucial to this accomplishment would be making use of Venus’ orbital movement and the moment it would come into a direct line between Earth and the sun. We’ll explore that further next time.
____________________________________
|