|
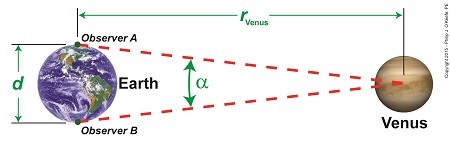
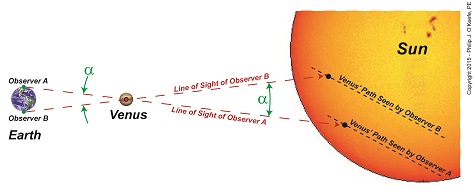
We’ve been paying a lot of attention to Venus and its orbital patterns, as did scientist Edmund Halley hundreds of years ago. Back then he came up with a plan to determine Earth’s distance to the sun, the AU. Two key components were Kepler’s Astronomical Unit, or AU, and an angle, α, which formed between lines of sight followed by observers on Earth during the Transit of Venus. Halley theorized that α together with Kepler’s Third Law of Planetary Motion would make it possible to calculate the AU. We’ll see how today. Figure 1 Figure 1 depicts what Halley had in mind. He theorized that if observers positioned on opposite sides of Earth could determine the precise times it took Venus to travel across the sun’s face from each of their perspectives, they could use this information together with previously gathered information on the time it takes Earth and Venus to make a complete orbit around the sun. This would allow the angle α to be calculated, and from that Earth’s distance to Venus, rVenus. Halley’s calculations for α are beyond the scope of this series, but if you’re interested in reading more about them, you can follow this link. Earth’s distance to Venus, rVenus, is computed in a manner similar to the method we used previously to determine Earth’s distance to the moon, by using this equation, r = d × tan(θ) For a refresher on the subject, follow this link to my past blog on Optically Measuring Cosmic Distances. And here’s the same equation modified to solve for the distance between Earth and Venus, rVenus, rVenus = d ÷ tan(α) (1) Once Earth’s distance to Venus was determined, its value was incorporated into Kepler’s equation for 1 AU, and the distance between Earth and the sun became known. Here again is the equation from Kepler’s Third Law of Planetary Motion, 1 AU = rVenus ÷ 0.28 (2) And here it is with the function for rVenus from equation (1) inserted into equation (2) to solve for 1 AU, 1 AU = [d ÷ tan(α)] ÷ 0.28 1 AU = d ÷ [0.28 × tan(α)] (3) From equation (3) the distance between Earth and the sun, 1 Astronomical Unit, was calculated to be between 92,000,000 and 96,000,000 miles. Unfortunately, a Transit of Venus did not occur within Halley’s lifetime, but scientists that followed him applied his methodology after the next Transit occurred in 1761. Since that time modern technology and the radar have improved measuring accuracy so that we now know the sun is located 92,935,700 miles from Earth. Next time we’ll return full circle to our opening topic in this long blog series when we reopen our discussion on gravity, specifically, how the concept of centripetal force is instrumental in determining the gravitational force exerted upon Earth by the sun.
____________________________________
|
Posts Tagged ‘Transit of Venus’
Calculating the Distance to the Sun
Thursday, June 25th, 2015Earth’s Distance to the Sun — A Roadmap
Thursday, June 18th, 2015|
We left off with Edmund Halley’s proposed method to solve the riddle of Earth’s distance to the sun. Halley posited that when Venus’ orbit brought it directly between the Earth and sun, then principles of astronomy, trigonometry, and geometry could be combined to calculate that distance. Instrumental to Halley’s theory were a number of elements discussed previously in this blog series, including the work of Johannes Kepler. We’ll mesh those elements today and chart the course for future discoveries. To begin things, Halley knew that Kepler’s Third Law of Planetary Motion set out the distance between Earth and the sun in theoretical terms as, 1AU = rVenus ÷ 0.28 which meant that if the distance from Earth to Venus, rVenus, could be calculated, then the distance from Earth to the sun was easily deduced, a matter of simple division. Crucial to the calculation of rVenus is to find the value for the angle α which forms between observers’ lines of sight while charting Venus’ travel across the face of the sun, something which only happens during a rare astronomical event known as the Transit of Venus. See Figure 1. Figure 1 Figure 1 shows two observers positioned on opposite sides of the Earth, busily surveying Venus’ movement across the sun’s face. Their lines of sight converge at a vertex point, or point of intersection, on Venus, then move beyond it to the sun. Due to the principle of vertical angles, which stipulates that angles which share the same vertex point also share the same angle measurement, we know that the angle α that’s formed between Observer A and B‘s lines of sight is of the same value between Earth and Venus as it is between Venus and the sun. Once a is determined, its numerical value can be plopped into an equation we’ve been working with for some time now in this blog series. It’s similar to the equation previously used to calculate Earth’s distance to the moon, r = d x tan(θ) Follow this link to Optically Measuring Cosmic Distances for a review. And here is that equation with terms modified to reflect our new quest, the distance from Earth to Venus, rVenus = d ÷ tan(α) As for the variable d, the distance between the two observers, we’ve worked with that before, too. Follow this link to Determining Chord Length on Circle Earth for a refresher. Next time we’ll see how Venus’ travel path is key to determining the angle α, shown in green on the illustration, and how this angle is crucial to our discovery of the distance between Earth and the sun.
____________________________________
|
The Transit of Venus from Different Perspectives
Wednesday, June 3rd, 2015|
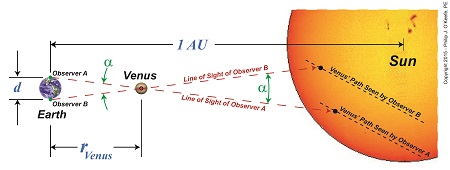
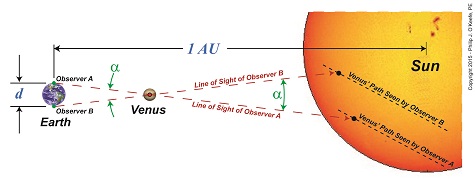
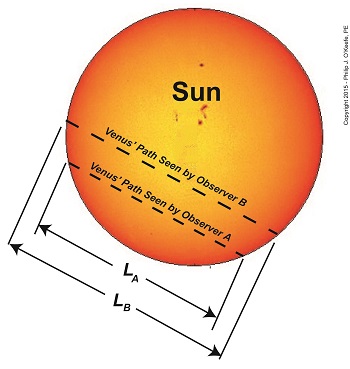
We’ve been working on calculating Earth’s distance to the sun and discussing how past scientists, including Johannes Kepler and Edmund Halley, contributed to the discussion. Today we’ll see how Halley used his theory on the transit of Venus together with Kepler’s Third Law of Planetary Motion and combined them with known mathematical principles to solve the riddle of this enormous distance, known as one astronomical unit, or AU. Halley’s solution began with stationing two observers with telescopes aimed at Venus on opposite sides of the Earth. Their different lines of sight would cause the principle of parallax to come into play, resulting in them seeing Venus from different perspectives. Their sight would converge at Venus’ center and an angle, α, would form between them. Halley posited that if this angle could be measured, it would be an important first step in calculating the distance between Earth and the sun. See Figure 1. Due to their differing perspectives, Observer A would see Venus traveling a path lower on the sun’s face, while Observer B would see it following a path higher up. See Figure 2. The net result was that the length, LA, of Venus’ path as seen by Observer A was significantly shorter than length, LB, of Venus’ path as seen by Observer B. Because of this, Observer B would have seen Venus pass in front of the sun before Observer A. These differing observations meant that even if both observers were to set their telescopic crosshairs on Venus at the exact same moment it became visible to each of them, it would serve no purpose, because they lacked a common point of reference at which to aim in order to take measurements. This fact made measuring the angle α with a physical device such as a protractor impossible. So Halley gave up on the idea of physically measuring α. Instead, he proposed calculating it based on the time it took for Observers A and B to watch Venus traverse the sun’s face from one side to the other along each of their observational paths. Next time we’ll see how Halley put his idea to work to calculate α and used it in conjunction with Kepler’s Third Law to calculate the AU.
____________________________________
|
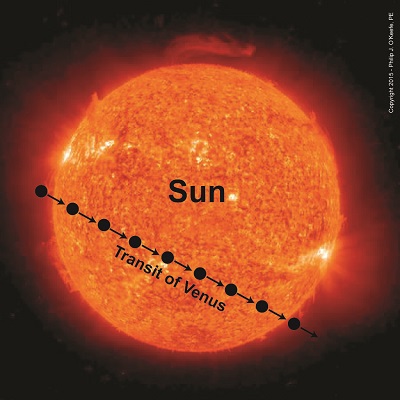
The Transit of Venus
Monday, May 18th, 2015|
Last time we learned of Johannes Kepler’s Third Law of Planetary Motion and his development of the astronomical unit (AU) and how these contributed to bringing ancient scientists a step closer to calculating Earth’s distance to the sun. Today we’ll see why Kepler’s focus on Venus, specifically its travel through space in relation to Earth and the sun — the so-called transit of Venus — would become the crucial element to solving the puzzle. Astronomers had previously used the Earth itself as an optical rangefinder to calculate distance to the moon. But unlike the moon which is relatively close to Earth, the sun is many tens of millions of miles away, too distant to be used in that manner. When it came to finding the distance from Earth to its sun, they were stumped. Then in 1716 Edmund Halley had the insight to combine Kepler’s Third Law and the parallax principle with Venus’ orbital journeys to devise an ingenious solution to the problem. The transit of Venus, first predicted by Kepler in 1627, is a rare astronomical phenomenon which only occurs every 243 years. At this time Venus becomes clearly visible from Earth and appears as a black dot traveling a straight path across the fiery backdrop of the sun’s surface. Figure 1 shows this phenomenon as it would look from Earth. According to Halley’s plan, two observers with telescopes would be positioned on opposite sides of the Earth. Due to the principle of parallax their lines of sight would provide different perspectives of Venus’ path. See Figure 2. From the perspective of Observer B, Venus’s path would appear higher on the sun’s face than the path seen from the perspective of Observer A. As their lines of sight converge on Venus’ center, an angle forms between them, which we’ll name α. The same angle forms as they look past Venus to the sun in its backdrop. Halley theorized that if the angle α could be measured, Kepler’s Third Law could be used together with trigonometry to calculate the distance between Earth and the sun, Kepler’s so-called AU. We’ll review Halley’s methodology next time.
____________________________________
|