|
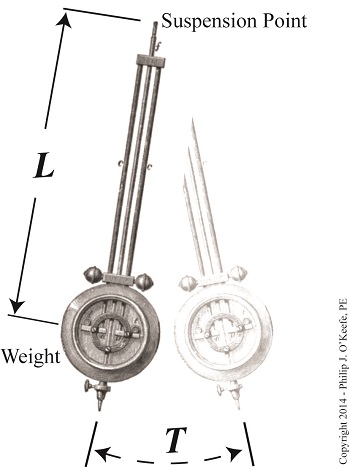
What would you do to pass the time if you were stuck on a ship of the middle ages for weeks at a time? Dutch mathematician Christiaan Huygens used the time to study the movement of clock pendulums. He watched them for endless hours, and he eventually came to realize that the pendulums’ swing was uneven due to the ship’s listing on the waves, a phenomenon which also affected the ship’s clocks’ accuracy. Eager to devise a solution to the problem of inaccurate time keeping, Huygens dedicated himself to finding a solution to the problem, and in so doing increase the navigational accuracy of ships as well. His efforts eventually resulted in a formula that shared a common variable with Isaac Newton’s gravitational formula, namely, g, Earth’s acceleration of gravity factor, a value which Huygens posited was indeed a non varying constant. Building upon Newton’s work, Huygens devised a formula which demonstrated the mathematical relationship between the motion of a clock’s pendulum and g. That formula is, T = 2 × ∏ × (L ÷ g)1/2 where, T is the period of time it takes a pendulum to make one complete swing, ∏ the Greek symbol pi, valued at 3.14, and L the length of the pendulum. Since devices capable of directly measuring the Earth’s gravity did not exist then, as they still don’t exist today, how in the world (pardon the pun) was Huygens able to arrive at this formula? Thinking outside the box, he posited that if one knows the length of the pendulum L, and then accurately measures the time it takes for the pendulum to complete its swings, taking into account the varied times that resulted due to the ship’s listing, one can calculate g using his equation. He eventually determined g‘s value to be equal to 32.2 feet per second per second, or 32.2 ft/sec2. Fast forwarding to Henry Cavendish’s time, Huygens’ work with pendulums and his determination of g was well known. We’ll see what Cavendish did with this knowledge next time.
_______________________________________
|
Archive for October, 2014
Huygens’ Use of Pendulums
Tuesday, October 21st, 2014|
Last time we learned that Henry Cavendish determined a value for G, the universal gravitational constant, fast on his way to determining a quantity he was determined to find, the Earth’s mass. Today we’ll see how the previous work of Christiaan Huygens, a contemporary of Isaac Newton’s, helped him get there. First Cavendish used algebra to rearrange terms in Newton’s gravitational formula so as to solve for M, Earth’s mass. Rearranged, Newton’s formula becomes, M = (g × R2) ÷ G But in order to solve for M, Cavendish first needed to know Earth’s acceleration of gravity, g. To aid him in this calculation he referred back to the work of Christiaan Huygens, a Dutch mathematician from Newton’s time. Huygens was eager to devise a formula capable of predicting clock pendulums’ motions on ships, his goal being to invent a timepiece accurate enough to make navigating ships easier. He hypothesized that a key factor in predicting a pendulum’s movement was an unknown constant, the acceleration of gravity factor, g, which Newton had previously posited existed. Through meticulous observation, Huygens came to realize that the time it took for pendulums to complete one swing back and forth was dependent not only on the length of the pendulum, but also this unknown quantity. In order for Huygens’ computations to work, the value of g had to be a constant, meaning, its value could not vary between computations; g‘s value was in fact a fudge factor, a phantom he would assign a specific numerical value. Huygens’ needed it in order to make his hypothesis work, a practice commonly use by scientists, even today. Determining a value for g would allow Huygens to successfully relate the length of the pendulum to the timing of its swing and to create a mathematical relationship between them. Huygens ultimately determined g’s value to be a whopping 32.2 feet per second per second, or 32.2 ft/sec2. We’ll see how he did it next time.
_______________________________________
|
How Big is the Earth?
Wednesday, October 8th, 2014|
Last time we discussed Isaac Newton’s Law of Gravitation and how he used it to arrive at conclusions concerning gravity. He theorized the existence of a universal gravitational constant, G, a set numerical value for all heavenly bodies in our universe, and he developed a formula to determine the acceleration of gravity, g. Newton felt sure that the gravity at play on the surface of any heavenly body, such as stars and planets, could be determined if one knew the value of G, along with the object’s mass, M, and radius, R, and he developed this equation to do so, g = (G × M) ÷ R2 At this point you may be thinking, Finding the mass and radius of a heavenly body is hard enough, but what is this universal gravitational constant?? Good point. Back in Newton’s time, the existence of G was purely speculative. He conceived it to be a numerical value which would act as a fudge factor, enabling his equation for determining g to work. As a matter of fact, Newton had no clue of how to determine G and was convinced that it would be beyond anyone’s ability to do so. The mysterious G factor and its numerical value were not actually determined until more than a hundred years later by Henry Cavendish. In 1796 Cavendish was focused on determining the Earth’s mass, M, by using Newton’s equation. To arrive at a value for G, Cavendish conducted experiments which measured the gravitational attraction between two lead spheres attached by way of a torsion balance. After much testing he eventually concluded that he had computed G to a reasonable degree of accuracy and that its value was equal to 3.439 x 10-8 cubic feet per slug per second squared. In this case a slug is not a slimy creature living in the garden, but rather a unit of measurement used to quantify the mass of an object. For the full story, see this article on Cavendish’s experiment by The Physics Classroom. But even after determining G, Cavendish still had to obtain values for g and R in order to calculate M. This was made possible thanks to the work of two men who came before him. One of these was the Greek mathematician Eratosthenes, who way back in 230 B.C. discovered that the radius of the earth, R, could be calculated by simply measuring the shadows of objects cast on Earth’s surface. All he needed was a measuring stick and geometry. For the full story see this fascinating article on the subject from Bucknell University. As for the value of g, the acceleration of gravity on Earth, Cavendish was aided by the previous efforts of a Dutch mathematician from Newton’s time, Christiaan Huygens. You may recall that Huygens was first introduced in a previous blog series on spur gear geometry, where we learned that he studied the motion of clock pendulums. Through observation, Huygens was able to arrive at a mathematical formula capable of predicting the pendulums’ often erratic motion on ships at sea. Next time we’ll see how Huygens’ insights gained by watching pendulums ultimately made it possible for him to arrive at a numerical value for Earth’s acceleration of gravity, g. _______________________________________
|