|
For some time now we’ve been analyzing the helpfulness of the engineering phenomena known as pulleys and we’ve learned that, yes, they can be very helpful, although they do have their limitations. One of those ever-present limitations is due to the inevitable presence of friction between moving parts. Like an unsummoned gremlin, friction will be standing by in any mechanical situation to put the wrench in the works. Today we’ll calculate just how much friction is present within the example compound pulley we’ve been working with. So How Much Friction is Present in our Compound Pulley?
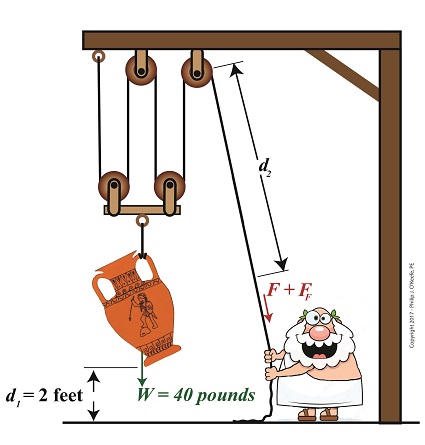
Last time we began our numerical demonstration of the inequality between a compound pulley’s work input, WI, and work output, WO, an inequality that’s due to friction in its wheels. We began things by examining a friction-free scenario and discovered that to lift an urn with a weight, W, of 40 pounds a distance, d1, of 2 feet above the ground, Mr. Toga exerts a personal effort/force, F, of 10 pounds to extract a length of rope, d2, of 8 feet. In reality our compound pulley must contend with the effects of friction, so we know it will take more than 10 pounds of force to lift the urn, a resistance which we’ll notate FF. To determine this value we’ll attach a spring scale to Mr. Toga’s end of the rope and measure his actual lifting force, FActual, represented by the formula, FActual = F + FF (1) We find that FActual equals 12 pounds. Thus our equation becomes, 12 Lbs = 10 Lbs + FF (2) which simplifies to, 2 Lbs = FF (3) Now that we’ve determined values for all operating variables, we can solve for work input and then contrast our finding with work output, WI = (F × d2) + (FF × d2) (4) WI = (10 Lbs × 8 feet) + (2 Lbs × 8 feet) (5) WI = 96 Ft-Lbs (6) We previously calculated work output, WO to be 80 Ft-Lbs, so we’re now in a position to calculate the difference between work input and work output to be, WI – WO = 16 Ft-Lbs (7) It’s evident that the amount of work Mr. Toga puts into lifting his urn requires 16 more Foot-Pounds of work input effort than the amount of work output produced. This extra effort that’s required to overcome the pulley’s friction is the same as the work required to carry a weight of one pound a distance of 16 feet. We can thus conclude that work input does not equal work output in a compound pulley. Next time we’ll take a look at a different use for pulleys beyond that of just lifting objects. Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |