Posts Tagged ‘weight’

Comparing Work Input to Output in a Compound Pulley

Monday, February 6th, 2017

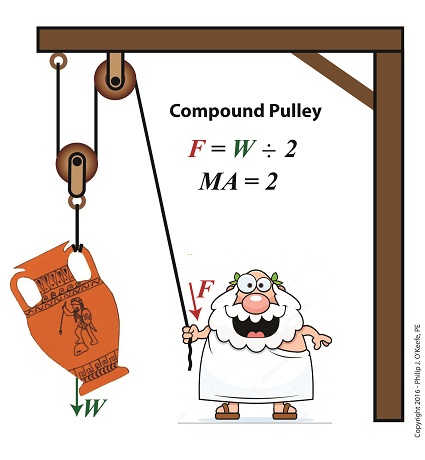
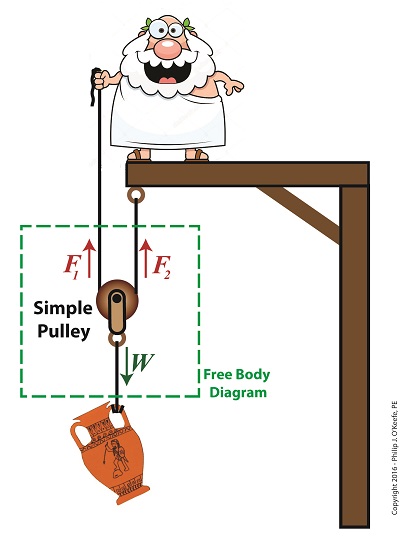
   Last time we performed an engineering analysis of a compound pulley which resulted in  an equation comparing the amount of true work effort, or work input, WI, required by machine or human to lift an object, in our case a toga’d man lifting an urn.   Our analysis revealed that, in real world situations, work input does not equal work output, WO, due to the presence of friction.   Today we’ll begin to numerically demonstrate their inequality by first solving for work output, and later work input.

Comparing Work Input to Output in a Compound Pulley

Comparing Work Input to Output in a Compound Pulley

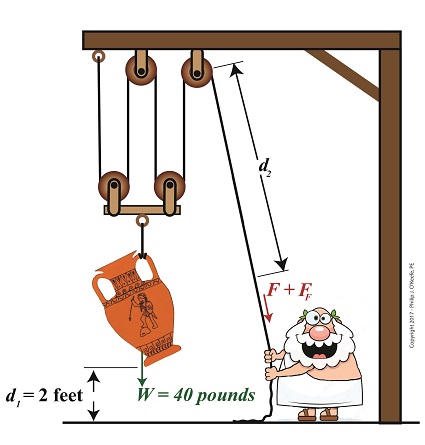
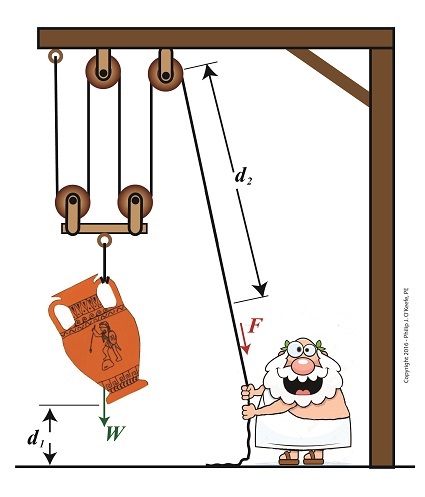
   To solve for the work output of our compound pulley, we’ll use an equation provided previously that is in terms of the variables W and d1,

WO = W × d1                                             (1)

   In our example Mr. Toga lifts an urn of weight, W, equal to 40 pounds to a height, or distance off the floor, d1, of 2 feet.   Inserting these values into equation (1) we arrive at,

WO = 40 pounds ×  2 feet = 80 Ft-Lbs          (2)

where, Ft-Lbs is a unit of work which denotes pounds of force moving through feet of distance.

   Now that we’ve calculated the work output, we’ll turn our attention to the previously-derived equation for work input, shown in equation (3).  Interrelating equations for WO and WI will enable us to solve for unknown variables, including the force, F, required to lift the urn and the length of rope, d2, extracted during lifting.  Once F and d2 are known, we can solve for the additional force required to overcome friction, FF,  then finally we’ll solve for WI.

   Once again, the equation we’ll be working with is,

WI = (F × d2) + (FF  × d2)                             (3)

   To calculate F, we’ll work the two terms present within parentheses separately, then use knowledge gained to further work our way towards a numerical comparison of work input and work output.   We’ll do that next time.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Comparing Work Input to Output in a Compound Pulley

Pulleys as a Work Input-Outut Device

Sunday, November 6th, 2016

    In our last blog we saw how adding extra pulleys resulted in mechanical advantage being doubled, which translates to a 50% decreased lifting effort over a previous scenario.    Pulleys are engineering marvels that make our lives easier.    Theoretically, the more pulleys you add to a compound pulley arrangement, the greater the mechanical advantage — up to a point.   Eventually you’d encounter undesirable tradeoffs.  We’ll examine those tradeoffs, but before we do we’ll need to revisit the engineering principle of work and see how it applies to compound pulleys as a work input-output device.

Pulleys as a Work Input-Outut Device

Pulleys as a Work Input-Outut Device

   

    The compound pulley arrangement shown includes distance notations, d1 and d2.   Their inclusion allows us to see it as a work input-output device.  Work is input by Mr. Toga, we’ll call that WI, when he pulls his end of the rope using his bicep force, F.   In response to his efforts, work is output by the compound pulley when the urn’s weight, W, is lifted off the ground against the pull of gravity.   We’ll call that work output WO.

    In a previous blog we defined work as a factor of force multiplied by distance.   Using that notation, when Mr. Toga exerts a force F to pull the rope a distance d2 , his work input is expressed as,

WI = F × d2

    When the compound pulley lifts the urn a distance d1 above the ground against gravity, its work output is expressed as,

WO = W × d1

    Next time we’ll compare our pulley’s work input to output to develop a relationship between d1 and d2.   This relationship will illustrate the first undesirable tradeoff of adding too many pulleys.

 Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Pulleys as a Work Input-Outut Device

Dynamic Lifting is Easier With a Compound Pulley

Friday, October 14th, 2016

    Last time we introduced the engineering concept of mechanical advantage, MA.   Thanks to its presence in our compound pulley arrangement, it made a Grecian man’s job of holding an urn suspended in space twice as easy as compared to when he used a mere simple pulley.   Today we’ll see what happens when our static scenario becomes active through dynamic lifting and how it affects his efforts.

Dynamic Lifting is Easier With a Compound Pulley

Dynamic Lifting is Easier With a Compound Pulley

    If you’ll recall from our last blog, Mr. Toga used a compound pulley to assist him in holding an urn stationary in space.   To do so, he only needed to exert personal bicep force, F, equivalent to half the urn’s weight force, W, which meant he enjoyed a mechanical advantage of 2.  Mathematically that is represented by,

F = W ÷ 2

If the urn weighs 40 pounds, then he only needs to exert 20 Lbs of personal effort to keep it suspended.

   But when Mr. Toga uses more bicep power with that same compound pulley, he’s able to dynamically raise its position in space until it eventually meets with the beam that supports it.   All the while he’ll be exerting a force greater than W ÷ 2.   That relationship is represented by,

F > W ÷ 2

    In the case of a 40 Lb urn, the lifting force Mr. Toga must exert to dynamically lift the urn is represented by,

F > 40 Lbs ÷ 2

F > 20 Lbs

where F represents a bicep force of at least 20 pounds.   Fortunately for him, his efforts will never have to extend much beyond 20 Lbs of effort to lift the urn to the beam.   That’s because gravity’s effect will remain nearly constant as the urn climbs, this being due to gravity’s influence upon objects decreasing by an insignificant amount over short distances above the Earth’s surface.   As a matter of fact, at an altitude of 3,280 feet, gravity’s pull decreases by a mere 0.2 %.

    The net result is that the compound pulley enables the same mechanical advantage whether a static or dynamic scenario exists, that is, regardless of whether Mr. Toga is simply holding the urn stationary in space or he’s actively tugging on his end of the rope to lift it higher.

    Next time we’ll see how mechanical advantage increases when we add more fixed and moveable pulleys to our compound pulley arrangement.

 Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Dynamic Lifting is Easier With a Compound Pulley

Mechanical Advantage of a Compound Pulley

Thursday, September 29th, 2016

    In this blog series on pulleys we’ve gone from discussing the simple pulley to the improved simple pulley to an introduction to the complex world of compound pulleys, where we began with a static representation.   We’ve used the engineering tool of a free body diagram to help us understand things along the way, and today we’ll introduce another tool to prepare us for our later analysis of dynamic compound pulleys.   The tool we’re introducing today is the engineering concept of mechanical advantage, MA, as it applies to a compound pulley scenario.

    The term mechanical advantage is used to describe the measure of force amplification achieved when humans use tools such as crowbars, pliers and the like to make the work of prying, lifting, pulling, bending, and cutting things easier.   Let’s see how it comes into play in our lifting scenario.

    During our previous analysis of the simple pulley, we discovered that in order to keep the urn suspended, Mr. Toga had to employ personal effort, or force, equal to the entire weight of the urn.

F = W                                    (1)

    By comparison, our earlier discussion on the static compound pulley revealed that our Grecian friend need only exert an amount of personal force equal to 1/2 the suspended urn’s weight to keep it in its mid-air position.   The use of a compound pulley had effectively improved his ability to suspend the urn by a factor of 2.   Mathematically, this relationship is demonstrated by,

F = W ÷ 2                              (2)

    The factor of 2 in equation (2) represents the mechanical advantage Mr. Toga realizes by making use of a compound pulley.   It’s the ratio of the urn’s weight force, W, to the employed force, F.   This is represented mathematically as,

MA = W ÷ F                            (3)

    Substituting equation (2) into equation (3) we arrive at the mechanical advantage he enjoys by making use of a compound pulley,

MA = W ÷ (W ÷ 2) = 2           (4)

Mechanical Advantage of a Compound Pulley

Mechanical Advantage of  a Compound Pulley

    Next time we’ll apply what we’ve learned about mechanical advantage to a compound pulley used in a dynamic lifting scenario.

 

 

 

                      

 Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Mechanical Advantage of a Compound Pulley

The Math Behind the Improved Simple Pulley

Tuesday, August 2nd, 2016

    Last time we introduced the free body diagram, applied it to a simple pulley, and discovered that in so doing lifting objects required 50% less effort.   As an engineering expert, I’ve sometimes put this improved version of a simple pulley to work for me in designs.   We’ll do the math behind the improvement today.

    Here again is the free body diagram showing the improved simple pulley as introduced last week.

The Improved Simple Pulley

The Math Behind the Improved Simple Pulley

     The illustration shows the three forces, F1, F2, and W, acting upon the simple pulley within the highlighted free body diagram.   Forces F1 and F2 are exerted from above and act in opposition to the downward pull of gravity, represented by the weight of the urn, W.   Forces F1 and F2  are produced by that which holds onto either end of the rope that’s threaded through the pulley.   In our case those forces are supplied by a man in a toga and a beam.   By engineering convention, these upward forces, F1 and F2, are considered positive, while the downward force, W, is negative.

    In the arrangement shown in our illustration, the pulley’s rope ends equally support the urn’s weight, as demonstrated by the fact that the urn remains stationary in space, neither moving up nor down.   In other words, forces F1 and F2 are equal.

    Now, according to the basic rule of free body diagrams, the three forces F1, F2, and W must add up to zero in order for the pulley to remain stationary.   Put another way, if the pulley isn’t moving up or down, the positive forces F1 and F2 are balancing the negative force presented by the urn’s weight, W.   Mathematically this looks like,

F1 + F2 – W = 0

or, by rearranging terms,

F1 + F2 = W

We know that F1 equals F2, so we can substitute F1 for F2 in the preceding equation to arrive at,

F1 + F1 = W

or,

2 × F1 = W

Using algebra to divide both sides of the equation by 2, we get:

F1 = W ÷ 2

Therefore,

F1 = F2 = W ÷ 2

    If the sum of the forces in a free body diagram do not equal zero, then the suspended object will move in space.   In our situation the urn moves up if our toga-clad friend pulls on his end of the rope, and it moves down if Mr. Toga reduces his grip and allows the rope to slide through his hand under the influence of gravity.

    The net real world benefit to our Grecian friend is that the urn’s 20-pound weight is divided equally between him and the beam.   He need only apply a force of 10 pounds to keep the urn suspended.

    Next time we’ll see how the improved simple pulley we’ve discussed today led to the development of the compound pulley, which enabled heavier objects to be lifted.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Math Behind the Improved Simple Pulley

The Force of Gravity

Thursday, November 20th, 2014

      Last time we saw how Henry Cavendish built upon the work of scientists before him to calculate Earth’s mass and its acceleration of gravity factor, as well as the universal gravitational constant.   These values, together with the force of gravity value, Fg, which we’ll introduce today, moved scientists one step further towards being able to discover the mass and gravity of any heavenly body in the universe.

      According to Newton’s Second Law of Motion, the force of gravity, Fg, acting upon any object is equal to the object’s mass, m, times the acceleration of gravity factor, g, or,

Fg = m × g

      So what is Fg?  It’s a force at play way up there, in the outer reaches of the galaxy, as well as back home.   It keeps the moon in orbit around the Earth and the Earth orbiting around the sun.   In the same way, Fg keeps us anchored to Earth, and if we were to calculate it, it would be calculated as the force of our body’s mass under the influence of Earth’s gravity.   It’s common to refer to this force as weight, but it’s not quite so simple.

      Using the metric system, the unit of measurement most often used for scientific analyses, weight is determined by multiplying our body’s mass in kilograms by the Earth’s acceleration of gravity factor of 9.8 meters per second per second, or 9.8 meters per second squared.

      For example, suppose your mass is 100 kilograms.   Your weight on Earth would be:

Weight = Fg = m × g = (100 kg) × (9.8 m/sec2) = 980 kg · m/sec2 = 980 Newtons

     Newtons?   That’s right.   It’s easier than saying kilogram · meter per second per second.   It’s also a way to pay homage to the man himself.

      In the English system of measurement things are perhaps even more confusing.   Your weight is found by multiplying the mass of your body measured in slugs by the Earth’s acceleration of gravity factor of 32 feet per second per second.   Slugs is British English speak for pounds · second squared per foot.   We normally refer to weight in units of  pounds, and in engineering circles it’s pounds force.

      For example, suppose your mass is 6 slugs, or 6 pounds · second squared per foot.   Your weight on Earth would be:

Weight = Fg = m × g = (6 Lbs · sec2/ft) × (32.2 ft/sec2)= 193.2 Lbs

      To avoid any confusion, you could just step on the bathroom scale.

Weight Force - Engineering Expert Witness

      Next time we’ll see how the force of gravity is influenced by an inverse proportionality phenomenon.

_______________________________________

Tags: , , , , , , , , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Force of Gravity