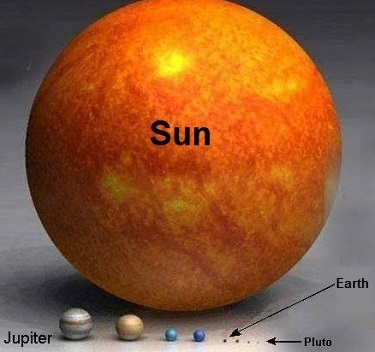
|
Last time we calculated the sun’s force of gravity acting upon Earth. It was the final unknown quantity within Newton’s equation to determine the mass of the sun, an equation we’ve been working with for some time now. Today we’re set to discover just how big the sun is. Newton’s formula, introduced in a past blog in this series entitled, Gravity and the Mass of the Sun is again, M = (Fg × r2) ÷ (m × G) where G is the universal gravitational constant as determined by Henry Cavendish and discussed in our blog, How Big is the Earth? and is equal to, G = 6.67 × 10-11 meters per kilogram • second2 As discussed in last week’s blog, The Sun’s Gravitational Force, Earth’s mass, m, its distance from the sun, r, and the force of the sun’s gravity acting upon Earth, Fg , are respectively, m = 5.96 × 1024 kilograms r = 149,000,000,000 meters Fg = 3.52 × 1022 Newtons Inserting these values into Newton’s equation to determine the mass, M, of the sun we get: M = [(3.52 × 1022) × (149,000,000,000)2] ÷ [(5.96 × 1024) × (6.67 × 10-11)] M = 1.96 × 1030 kilograms So how big is 1.96 × 1030 kilograms? To get a better idea, let’s divide the sun’s mass, M, by the Earth’s mass, m, (1.96 × 1030 kilograms) ÷ (5.96 × 1024 kilograms) = 328,859.06 That’s a big number, and it translates to the sun being over 300,000 times more massive than Earth. The picture below displays this comparison in stunning visual terms.
Once 19th Century scientists had calculated the mass of the sun, they went on to calculate the masses of other heavenly bodies in our solar system and the gravitational forces at play on each of them. Armed with this information mankind was able to subsequently build exploratory probes capable of extending their reach into the far unknowns of our solar system and beyond. This ends our discussion on gravity within our solar system. Next time we’ll return to Earth and begin exploring the physics behind falling objects.
____________________________________
|
Posts Tagged ‘Sir Isaac Newton’
How Big is the Sun?
Monday, August 10th, 2015
The Sun’s Gravitational Force
Monday, August 3rd, 2015|
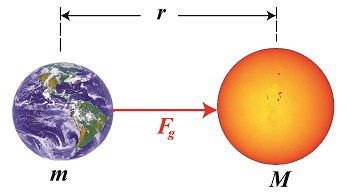
Last time we discovered that Earth zips around the sun at the mind boggling speed of 29,680 meters per second. This is the final bit of information required to calculate Fg, the gravitational force exerted upon Earth by its sun, as set out in Newton’s equation on the subject and derived from his Second Law of Motion. We’ll calculate that quantity today. Newton’s formula that we’ll be working with is, Fg = [m × v2] ÷ r where Earth’s speed, or orbital velocity, is the v in the equation. The other variables, m and r, have previously been determined in this blog series. For a refresher see Centripital Force Makes the Earth Go Round, What is Earth’s Mass, and Calculating the Distance to the Sun. Earth’s mass, m, is valued at 5.96 × 1024 kilograms, while r is Johannes Kepler’s astronomical unit, equal to about 149,000,000,000 meters. Inserting these numerical values into Newton’s equation to determine the sun’s gravitational force acting upon Earth we arrive at, Fg = [(5.96 × 1024 kilograms) × (29,680 meters per second)2] ÷ 149,000,000,000 meters Fg = 3.52 × 1022 kilogram • meter per second2 This metric unit of force, kilogram • meter per second2, represents kilograms multiplied by meters, and their product divided by seconds squared. It’s known in scientific circles as the Newton, in honor of Sir Isaac Newton, widely recognized as one of the greatest scientists of all time and a key figure in the scientific revolution that began over three centuries ago. Therefore the sun’s gravitational force acting upon Earth is typically referred to as, Fg = 3.52 × 1022 Newtons Here in the US where we like to use English units such as feet and pounds, the Newton is said to equal 0.225 pounds of force. Therefore in English units the sun’s gravitational force is expressed as, Fg = (3.52 × 1022 Newtons) × (0.225 pounds of force per Newton) Fg = 7.93 × 1021 pounds That’s scientific notation for 7,930,000,000,000,000,000,000 pounds! That’s the amount of force exerted by the sun’s gravitational pull on Earth. Seems about right — right?
Now that we know Fg, we have everything we need to calculate the mass of the sun, which in turn enables us to determine the mass and gravity of other planets in our solar system. We’ll calculate the sun’s mass next time. ____________________________________
|
Gravity and the Mass of the Sun
Friday, December 12th, 2014|
As a young school boy I found it hard to believe that scientists were able to compute the mass of our sun. After all, a galactic-sized measuring device does not exist. But where there’s a will, there’s a way, and by the 18th Century scientists had it all figured out, thanks to the work of others before them. Newton’s two formulas concerning gravity were key to later scientific discoveries, and we’ll be working with them again today to derive a third formula, bringing us a step closer to determining our sun’s mass. Newton’s Second Law of Motion allows us to compute the force of gravity, Fg, acting upon the Earth, which has a mass of m. It is, Fg = m × g (1) Newton’s Universal Law of Gravitation allows us to solve for g, the sun’s acceleration of gravity value, g = (G × M) ÷ r2 (2) where, M is the mass of the sun, r is the distance between the sun and Earth, and G is the universal gravitational constant.
You will note that g is a common factor between the two equations, and we’ll use that fact to combine them. We’ll do so by substituting the right side of equation (2) for the g in equation (1) to get, Fg = m × [(G × M) ÷ r2] then, using algebra to rearrange terms, we’ll set up the combined equation to solve for M, the sun’s mass: M = (Fg × r2) ÷ (m × G) (3) At this point in the process we know some values for factors in equation (3), but not others. Thanks to Henry Cavendish’s work we know the value of m, the Earth’s mass, and G, the universal gravitational constant. What we don’t yet know is Earth’s distance to the sun, r, and the gravitational attractive force, Fg, that exists between them. Next time we’ll introduce some key scientists whose work contributed to a method for computing the distance of our planet Earth to its sun. _______________________________________
|
The Force of Gravity
Thursday, November 20th, 2014|
Last time we saw how Henry Cavendish built upon the work of scientists before him to calculate Earth’s mass and its acceleration of gravity factor, as well as the universal gravitational constant. These values, together with the force of gravity value, Fg, which we’ll introduce today, moved scientists one step further towards being able to discover the mass and gravity of any heavenly body in the universe. According to Newton’s Second Law of Motion, the force of gravity, Fg, acting upon any object is equal to the object’s mass, m, times the acceleration of gravity factor, g, or, Fg = m × g So what is Fg? It’s a force at play way up there, in the outer reaches of the galaxy, as well as back home. It keeps the moon in orbit around the Earth and the Earth orbiting around the sun. In the same way, Fg keeps us anchored to Earth, and if we were to calculate it, it would be calculated as the force of our body’s mass under the influence of Earth’s gravity. It’s common to refer to this force as weight, but it’s not quite so simple. Using the metric system, the unit of measurement most often used for scientific analyses, weight is determined by multiplying our body’s mass in kilograms by the Earth’s acceleration of gravity factor of 9.8 meters per second per second, or 9.8 meters per second squared. For example, suppose your mass is 100 kilograms. Your weight on Earth would be: Weight = Fg = m × g = (100 kg) × (9.8 m/sec2) = 980 kg · m/sec2 = 980 Newtons Newtons? That’s right. It’s easier than saying kilogram · meter per second per second. It’s also a way to pay homage to the man himself. In the English system of measurement things are perhaps even more confusing. Your weight is found by multiplying the mass of your body measured in slugs by the Earth’s acceleration of gravity factor of 32 feet per second per second. Slugs is British English speak for pounds · second squared per foot. We normally refer to weight in units of pounds, and in engineering circles it’s pounds force. For example, suppose your mass is 6 slugs, or 6 pounds · second squared per foot. Your weight on Earth would be: Weight = Fg = m × g = (6 Lbs · sec2/ft) × (32.2 ft/sec2)= 193.2 Lbs To avoid any confusion, you could just step on the bathroom scale.
Next time we’ll see how the force of gravity is influenced by an inverse proportionality phenomenon. _______________________________________
|
What is Earth’s Mass?
Friday, November 7th, 2014|
Last time we learned how Henry Cavendish used Christiaan Huygens’ work with pendulums to determine the value of g, the acceleration of gravity factor for Earth, to be 32.3 ft/sec2, or 9.8 m/sec2. From there Cavendish was able to go on and arrive at values for other factors in Isaac Newton’s gravity formula, namely G, the universal gravitational constant, and M, Earth’s mass. Today, we’ll discuss how Cavendish was able to calculate the Earth’s mass. Newton’s formula for gravity, once again, is: M = (g × R2) ÷ G where M stands for the mass of the heavenly body being quantified. For our case today M will represent the mass of Earth, which was originally quantified in slugs, a British unit of measurement. Today the measurement unit of choice in most parts of the world is the kilogram, which is the metric equivalent of a slug. With regard to the other variables in Newton’s gravity formula, namely, R and G, their values had previously been determined. Eratosthenes’ measurement of shadows cast by the sun on Earth’s surface had revealed Earth’s radius, R, to be 6,371 kilometers, or 6,371,000 meters. And Cavendish’s experiments led him to conclude that the universal gravitational constant, G, was 6.67 × 10-11 cubic meters per kilogram-second squared. Plugging these values into Newton’s equation, we calculate Earth’s mass to be: M = ((9.8 m/sec2) × (6,371,000 m)2) ÷ (6.67 × 10-11 m3/kg-sec2) M = 5.96 × 1024 kilograms Incidentally, 5.96 × 1024 is scientific notation, or mathematical shorthand, for the number 5,960,000,000,000,000,000,000,000. That’s a whole lot of zeros! Calculating the mass of Earth was an impressive accomplishment. Now that its value was known, scientists would be able to calculate the mass and acceleration of gravity for any heavenly body in the universe. We’ll see how that’s done next time.
_______________________________________
|
Mechanical Power Transmission – The Centrifugal Clutch in Operation
Sunday, April 22nd, 2012| Just the other day I unexpectedly experienced the effects of centrifugal force while driving home from the grocery store. The checker had packed my entire order into one bag, making it top heavy. Then en route someone cut me off at an intersection, and I had to make a sharp turn to avoid a crash. During this maneuver centrifugal force came into play, forcing my grocery bag out of its centered position on the front seat next to me. It lurched into the passenger’s door, fell over, and spilled its contents onto the floor. Fortunately the eggs didn’t get smashed.
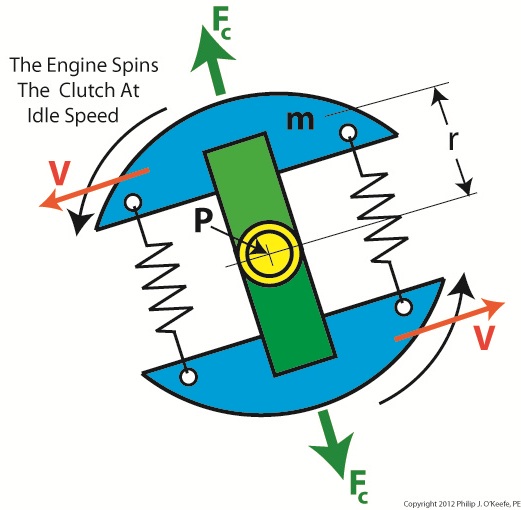
In previous articles we identified the component parts of a centrifugal clutch mechanism and learned how centrifugal force makes objects spinning in a circular path about a fixed point move outward. We can now explore what happens when we couple a centrifugal clutch mechanism to the engine of a grass trimmer. Figure 1 depicts the spinning clutch mechanism of a gas engine when it’s just been started and is operating at a slow idle speed.
Figure 1
Like the red ball in my previous article on centrifugal force, the blue centrifugal clutch shoes each have a mass m. They spin around a fixed point P, situated at the center of the yellow engine shaft coupling. Point P is located a distance r from the center of each shoe. The shoes in motion have a tangential velocity V, and in accordance with Sir Isaac Newton’s Law of Centrifugal Force, the force Fc acts upon each shoe, causing them to want to pull out from the center of the mechanism, away from the fixed point. Since idle speed is rather slow, however, the centrifugal force exerted upon the shoes isn’t strong enough to overcome the tension of the two springs and the coils connecting them remain coiled, holding the shoes tightly in position on the green boss. So what happens when we press the throttle trigger on the gas engine and cause the engine to speed up? See Figure 2.
Figure 2
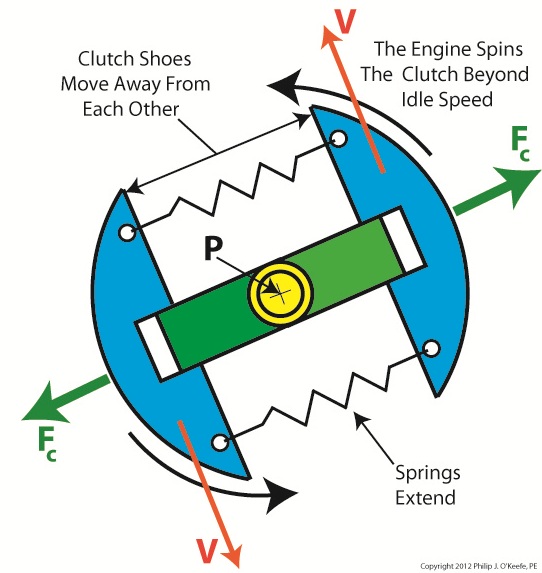
Figure 2 shows the clutch mechanism spinning at an increased velocity. The tangential velocity V increases, and according to Newton’s law, the centrifugal force Fc acting on the clutch shoes increases as well. The force is so strong that it overcomes the tension in the springs and they extend. The clutch shoes are caused to move out and away from fixed point P, as well as from each other, traveling along the ends of the boss. When we remove our finger from the throttle trigger, the engine will slow down and return to idle speed. The centrifugal force will decrease and the springs will pull the shoes back towards fixed point P. The mechanism will return to its previous state, as shown in Figure 1. Next time we’ll insert the centrifugal clutch mechanism into the clutch housing to see how mechanical power is transmitted from the engine to the cutter head in our grass trimmer. ____________________________________________
|
Mechanical Power Transmission – Centrifugal Force and Centrifugal Clutches
Monday, April 9th, 2012| I’m not a big fan of amusement parks. The first time I rode on a Tilt-A-Whirl I was caught off guard and flung onto my side by the centrifugal force acting upon my body, the lower half of which was constrained by a seat belt so I wouldn’t be catapulted out during the ride. To make matters worse, the centrifugal force started to force the lunch I’d made the mistake of eating just before back up my throat. It was a very unpleasant experience to say the least.
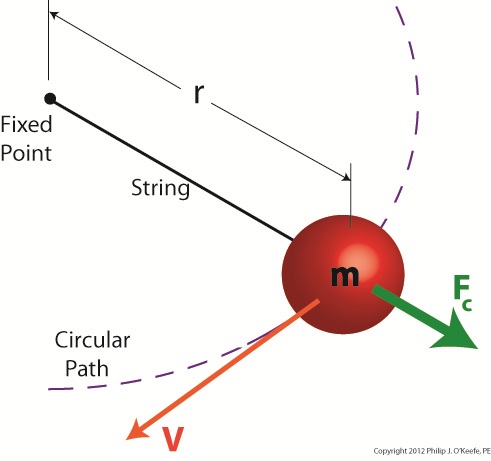
Centrifugal force is an interesting phenomenon, and its principles are involved in the operation of a centrifugal clutch, which we’ll see later. For now, let’s get a basic understanding of what it’s all about, thanks to the discoveries of Sir Isaac Newton in the late 17th Century. Figure 1
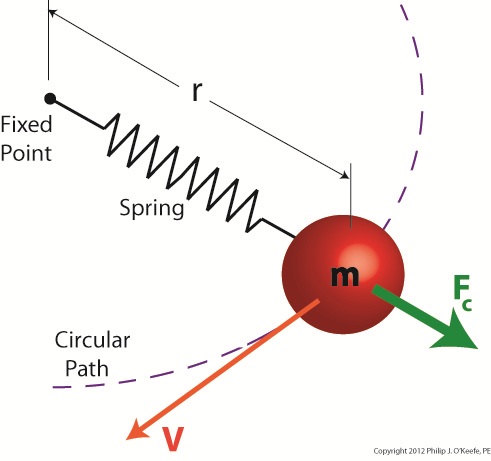
Figure 1 shows a red ball, whose mass we’ll notate m, attached to a string, the other end of which is attached to a fixed point, such as if you held it taught between your fingers. If you’re in a playful mood, you might enjoy twirling the ball above your head on its string. The distance between the center of the ball and the fixed point is labeled r, which stands for the radius of the circular path traveled by the ball as it twirls around the fixed point. The speed at which the ball travels through the air is called its straight line velocity, or tangential velocity in scientific-speak, and it is generally notated as a V. The centrifugal force, or Fc, that is exerted upon the ball as it whirls around your head is, Sir Isaac tells us, measured by the equation: Fc = mV2/r Centrifugal force in the simplest of terms is an outward-pushing force that pulls objects in motion away from the point about which they’re rotating. Let’s hold as fact that if m and r don’t change, then Newton’s equation tells us that the centrifugal force exerted upon the object in motion increases by the square of the velocity, or speed, of the ball. In other words, the faster the ball moves as you spin it around your head on the string, the harder the centrifugal force that acts upon it. As you spin the ball faster and faster, it will pull outward more and more strenuously, exerting ever greater resistance upon the string you hold between your fingers. Now suppose we replace the string in this example with a spring as shown in Figure 2.
Figure 2
Why a spring? Because that’s what’s used within a centrifugal clutch. Just as with the string, the ball’s velocity increases as you increase rotation speed around the fixed point, and the centrifugal force acting upon its mass by the spinning action increases as well. The spring expands, extending further and further out from its beginning position of attachment to the fixed point, your fingers. As velocity decreases, the spring will retract, eventually returning to its original coil size. This extending and retracting action is the major mechanism at play within a centrifugal clutch. Next time we’ll explore a centrifugal clutch mechanism in more depth to observe its behavior relative to its spring under the influence of centrifugal force. ____________________________________________
|
Vibration Analysis in Mechanical Engineering, Part II
Sunday, March 14th, 2010|
Last week we began a new article on vibration analysis. This week we’ll continue by looking at how to solve a vibration analysis problem. Analysis of vibration in machine designs typically involves advanced knowledge of kinetics and higher level mathematics like calculus. For this discussion, let’s consider a relatively simple balancing problem for a rotating system of masses. Suppose you have a ball with 10kg of mass on the end of a stick. If you’ll recall from our discussion about kinetics, mass is the weight of an object divided by the acceleration of gravity. For this problem, let’s say that only the ball has mass and not the stick. Although this may seem nonsensical, it is necessary in order not to complicate our analysis well beyond the basic discussion we are having here. Getting back to our ball and stick combo, the other end of the stick is attached to a rotating shaft, and the center of the ball is 0.5 meters (m) away from the center of the shaft. This rotating system is shown in Figure 1. Figure 1 – A Rotating System With One 10kg Ball
When the shaft rotates at 60 revolutions per minute (RPM), the ball moves in a circle around the shaft via the stick as shown in Figure 2. The centrifugal force created by the circular motion of the ball always points at a 90 degree angle to the ball’s path of movement. The net result is an effect similar to that felt when you drive quickly around a sharp right-hand curve and you feel as though you are being pushed to one side.
Figure 2 – Side View of the Rotating System in Figure 1
Getting back to Figure 2, since the centrifugal force is at a 90 degree angle to its movement, it keeps changing direction. When the ball is at the top of its movement, the force points straight up as shown in (a). When the ball is horizontal right, the force points right as shown in (b). When the ball is at the bottom of its movement, the force points down as shown in (c). When the ball is horizontal left, the force points left as shown in (d). This change in the direction of the centrifugal force pulls the rotating system up, to the right, down, and to the left as the shaft rotates, causing vibration in the whole system. The mechanics of this vibration are very similar to the unbalanced load in the washing machine during spin cycle that we talked about last week. To answer this question, let’s apply the formula for centrifugal force on a ball as it rotates in our system above: F = (Mass) x ((RPM) x (1 min. / 60 sec.))2 x (4 π2) x (Distance From Center of Rotation) Plugging in values, the centrifugal force for the 10kg ball is calculated to be: F10kg = (10 kg) x ((60 RPM) x (1 min. / 60 sec.))2 x (4 π2) x (0.5 m) = 197.39 kg m/sec2 = 197.39 Newtons In case you’re wondering, scientists got tired of talking about the metric units of force as “kg m/sec2,” so they decided to rename these units in honor of the great Sir Isaac Newton. In order for the vibration in our example to go away, the centrifugal force for the 10kg ball must equal the centrifugal force of the 6kg ball. Knowing this, we can work backwards to calculate the distance from the center of rotation for the 6kg ball. This distance will be key to balancing the system out because it acts to compensate for the unequal masses of the balls. F6kg = 197.39 kg m/sec2 = (6 kg) x ((60 RPM) x (1 min. / 60 sec.))2 x (4 π2) x (Distance From Center of Rotation6kg) And the distance from the center of rotation becomes: Distance From Center of Rotation6kg = 197.39 kg m/sec2 /[(6 kg) x ((60 RPM) x (1 min. / 60 sec.))2 x (4 π2)] = 0.83 meters This tells us that we’d have to cut our stick so that the center of the 6kg ball is 0.83 meters from the center of the shaft in order to compensate for the vibration caused by the rotating 10kg ball. See Figure 3.
Figure 3 – A Rotating System With One 10kg Ball and One 6kg Ball This concludes our basic look at vibration analysis. Next week we’ll get into the last installment of our mechanical engineering series to see how everything we’ve learned throughout this series ties together in machine design. _________________________________________________________________ |
