|
Last week we began a new article on vibration analysis. This week we’ll continue by looking at how to solve a vibration analysis problem.
Analysis of vibration in machine designs typically involves advanced knowledge of kinetics and higher level mathematics like calculus. For this discussion, let’s consider a relatively simple balancing problem for a rotating system of masses.
Suppose you have a ball with 10kg of mass on the end of a stick. If you’ll recall from our discussion about kinetics, mass is the weight of an object divided by the acceleration of gravity. For this problem, let’s say that only the ball has mass and not the stick. Although this may seem nonsensical, it is necessary in order not to complicate our analysis well beyond the basic discussion we are having here. Getting back to our ball and stick combo, the other end of the stick is attached to a rotating shaft, and the center of the ball is 0.5 meters (m) away from the center of the shaft. This rotating system is shown in Figure 1.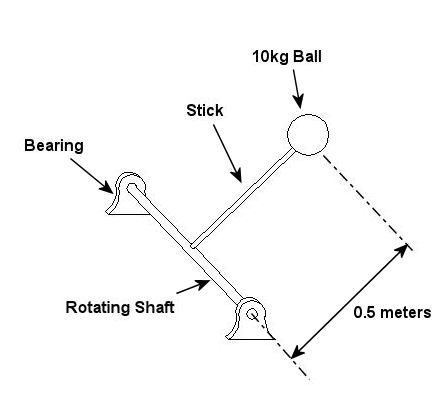
Figure 1 – A Rotating System With One 10kg Ball
When the shaft rotates at 60 revolutions per minute (RPM), the ball moves in a circle around the shaft via the stick as shown in Figure 2. The centrifugal force created by the circular motion of the ball always points at a 90 degree angle to the ball’s path of movement. The net result is an effect similar to that felt when you drive quickly around a sharp right-hand curve and you feel as though you are being pushed to one side.
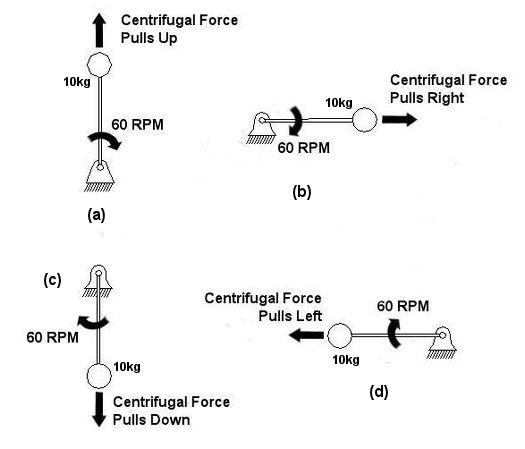
Figure 2 – Side View of the Rotating System in Figure 1
Getting back to Figure 2, since the centrifugal force is at a 90 degree angle to its movement, it keeps changing direction. When the ball is at the top of its movement, the force points straight up as shown in (a). When the ball is horizontal right, the force points right as shown in (b). When the ball is at the bottom of its movement, the force points down as shown in (c). When the ball is horizontal left, the force points left as shown in (d). This change in the direction of the centrifugal force pulls the rotating system up, to the right, down, and to the left as the shaft rotates, causing vibration in the whole system. The mechanics of this vibration are very similar to the unbalanced load in the washing machine during spin cycle that we talked about last week.
To answer this question, let’s apply the formula for centrifugal force on a ball as it rotates in our system above:
F = (Mass) x ((RPM) x (1 min. / 60 sec.))2 x (4 π2) x
(Distance From Center of Rotation)
Plugging in values, the centrifugal force for the 10kg ball is calculated to be:
F10kg = (10 kg) x ((60 RPM) x (1 min. / 60 sec.))2 x (4 π2) x (0.5 m)
= 197.39 kg m/sec2 = 197.39 Newtons
In case you’re wondering, scientists got tired of talking about the metric units of force as “kg m/sec2,” so they decided to rename these units in honor of the great Sir Isaac Newton.
In order for the vibration in our example to go away, the centrifugal force for the 10kg ball must equal the centrifugal force of the 6kg ball. Knowing this, we can work backwards to calculate the distance from the center of rotation for the 6kg ball. This distance will be key to balancing the system out because it acts to compensate for the unequal masses of the balls.
F6kg = 197.39 kg m/sec2 = (6 kg) x ((60 RPM) x (1 min. / 60 sec.))2 x
(4 π2) x (Distance From Center of Rotation6kg)
And the distance from the center of rotation becomes:
Distance From Center of Rotation6kg =
197.39 kg m/sec2 /[(6 kg) x ((60 RPM) x (1 min. / 60 sec.))2 x (4 π2)]
= 0.83 meters
This tells us that we’d have to cut our stick so that the center of the 6kg ball is 0.83 meters from the center of the shaft in order to compensate for the vibration caused by the rotating 10kg ball. See Figure 3.
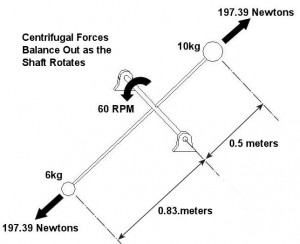
Figure 3 – A Rotating System With One 10kg Ball and One 6kg Ball
This concludes our basic look at vibration analysis. Next week we’ll get into the last installment of our mechanical engineering series to see how everything we’ve learned throughout this series ties together in machine design.
_________________________________________________________________ |