Engineering Expert Witness Blog

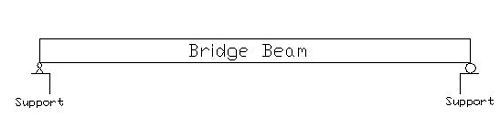
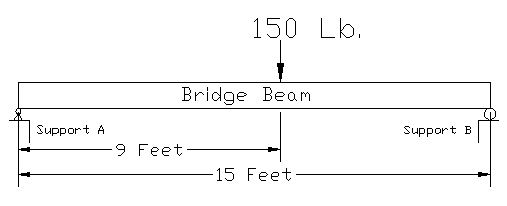
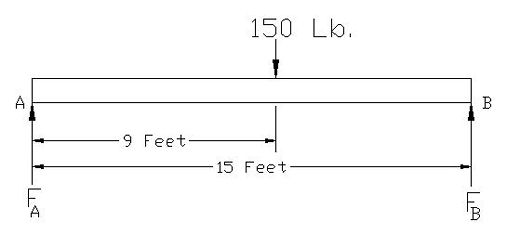
     As I stated in my last blog post, Statics is the study of how forces are transmitted to and throughout stationary objects.  Let’s learn a little bit about  how statics is used by mechanical engineers to solve problems.

     Consider a perfectly rigid bridge beam sitting on two supports (see Figure 1).  Now suppose you decide to stand on it.  The weight of your body would push down on the beam, creating a system of forces that act upon the beam.  If the beam stays on its supports and doesn’t move (it remains static), then the forces are said to be in “equilibrium.”  In other words, since the beam doesn’t move when you stand on it, the sum of all the forces acting upon it are zero.

Figure 1

     So what, you say?  Well, this concept of forces in equilibrium helps mechanical engineers analyze external and internal forces acting on stationary objects that have importance to us in real life, like bridges, machines, traffic signal masts, etc.  This analysis is used to calculate the magnitudes of all the forces acting on these objects so they can design parts of the objects to be strong enough not to break apart.  Think about that next time you get ready to cross a bridge in your car.

     To show how this works, consider the bridge beam scenario I discussed above.  Suppose you weigh 150 pounds and you stand nine feet from the left end of the bridge beam (see Figure 2).  Your weight will exert a downward force of 150 pounds upon the beam (let’s ignore the weight of the beam in this case).   The weight of your body creates reaction forces on the beam at Support A and Support B.  To consider these reaction forces, the mechanical engineer would draw what is called a “free body diagram” (see Figure 3).

Figure 2

Figure 3

     The reaction forces (F_A and F_B) at the supports A and B push up on the bottom of the beam.  If the beam remains static, then the sum of the reaction forces will equal the 150 pound weight force from your body.  That is, the reaction forces cancel out the 150 pound force if the beam doesn’t move and they are said to be in equilibrium.

     But in our example above, you’re not standing in the exact center of the beam, hence the two reaction forces are not going to be equal.  More of your body weight force is bearing down on Support B and less on Support A.  So how do you determine the values of the reaction forces in a situation like this?  You consider “moments.”

     A moment is mechanical engineering lingo for a force multiplied by a distance.  Moments want to rotate objects.  This is an important concept in statics because if an object doesn’t move, it certainly won’t rotate, so the sum of all the moments acting on the object are zero.  So, in the case of our bridge beam, the sum of the moments acting on Support A would be zero, or mathematically speaking:

Sum M_A = [(F_A) x (0 Feet)] – [(150 Lb.) x (9 Feet)] + [(F_B) x (15 Feet)] = 0 

Using algebra, you can find the value for the reaction force at Support B:

[0] – [(150 Lb.) x (9 Feet)] + [(F_B) x (15 Feet)] = 0

[(F_B) x (15 Feet)] = [(150 Lb.) x (9 Feet)]

F_B = 90 Lb.

     So what about the reaction force at Support A?  If you remember, I said that if the bridge beam remains static, then the sum of all the forces acting on it will be zero.  Knowing that, you can use algebra to solve for the reaction force at Support A:

F_A -150 Lb + F_B = 0

F_A = 150 Lb. – 90 Lb. = 60 Lb.

     So that is the basic concept of statics.  Remember, in statics, nothing moves, so mechanical engineers use that to their advantage when they analyze forces acting on objects.

     Our next topic will be:  Dynamics, the study of the effects of velocity and acceleration and resulting forces and the energy of moving objects.
_________________________________________________________________

Last week’s Riddle:  Everyone knows us to be racing by when they look at a clock, but mechanical engineers also know us to add up to zero when they look at a fixed structure.  What are we?

Answer:  Moments

_________________________________________________________________