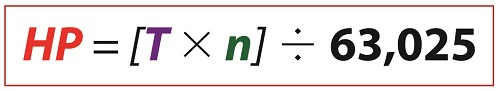Archive for November, 2017

Horsepower Required to Accelerate a Flywheel

Friday, November 24th, 2017

    Last time we discussed how torque is created as a flywheel spins.   This torque is a factor of the flywheel’s moment of inertia, which is dependent on how far the masses of the flywheel’s parts are located from its center of rotation.   Today we’ll present a formula to compute how much horsepower is required to accelerate a flywheel.   And here it is,

Horsepower Required to Accelerate a Flywheel

Horsepower Required to Accelerate a Flywheel

where, T is the torque created on the flywheel’s shaft in units of inch-pounds.   The term n is the flywheel shaft’s speed of rotation in revolutions per minute, RPM.   Horsepower, HP, is engineering shorthand for a unit of power equal to 6600 inch-pounds per second, and the number 63,025 is a constant needed to convert torque, T, and the spinning shaft’s rotations per minute, RPM, into horsepower units.

    Torque is present whether the flywheel’s spin accelerates or decelerates.   During acceleration torque is created, which contributes to the production of kinetic energy that’s stored inside the flywheel.  When a flywheel’s spin decelerates, its mass experiences the effects of negative acceleration, and stored kinetic energy is released.

    As we learned awhile back, horsepower is a function of torque in any moving machinery, including engines and flywheels.  An engine must produce horsepower to accelerate a flywheel connected to its shaft.   By the same token, when the engine’s horsepower output diminishes or stops, the flywheel begins to decelerate.   This deceleration causes kinetic energy stored within the flywheel to be released, providing horsepower necessary to keep the engine and flywheel spinning.   That is, until the power output of the engine returns or the stored kinetic energy of the flywheel is ultimately exhausted.

    We’ll see how that works next time when we take a look inside a reciprocating engine.

opyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Horsepower Required to Accelerate a Flywheel

Flywheel Torque and Distribution of Mass

Monday, November 13th, 2017

    Last time we began our discussion on moment of inertia and how it affects a flywheel’s storage of kinetic energy.   That inertia is a function of the flywheel’s mass, in particular how the mass is distributed.   Today we’ll continue our discussion and see how an engineering principal known as torque affects things.

Flywheel Torque and Distribution of Mass

Flywheel Torque and Distribution of Mass

   

    We learned in a previous blog that torque is most simply defined as a measure of how much force acts upon an object to cause it to rotate around a pivot point or center of rotation, shown as a small black dot in the illustration.   For our discussion we’ll focus on two parts of the flywheel, the hub, part A, and the rim, part E.

    Part A has a mass mA located a distance rA from the flywheel’s center, while part E has a mass mE located a distance rE from it.   When an engine applies mechanical power to the flywheel by way of its rotating shaft, the revolutions per minute, RPM, increase and along with it the angular velocity, ω, also increases.   For a refresher on this, follow the link.

    Because of this relationship, we can calculate the kinetic energy contained within a flywheel using the kinetic energy formula,

KE = ½ × ∑[m × r2] × ω2               (1)

    As the flywheel’s angular velocity increases or decreases in response to the engine’s energy output, parts A and E reflect acceleration or deceleration of aA and aE.   Since parts A and E exhibit both mass and acceleration, they are subject to Newton’s Second Law of Motion, which states that force equals mass times acceleration.   Using that relationship we can calculate the force exerted on each part by,

FA = mA ×  aA                                  (2)

FE = mE ×  aE                                  (3)

    Part A is small compared to part E, therefore mE is greater than mA and accordingly FE is greater than FA.   Forces FA and FE act as torques, because they cause parts A and E to rotate around the flywheel’s center of rotation, so they are designated as Torque A, TA, and Torque E, TE.    These torques are computed by,

TA = FA ×  rA                                   (4)

TE = FE ×  rE                                   (5)

    Part E’s greater mass will contribute more torque than part A, and it will also contribute more to the flywheel’s kinetic energy content.

    Most flywheels are designed with heavy rims supported by small hubs and slender spokes, because the more mass that’s distributed away from the flywheel’s center of rotation, the greater the flywheel’s moment of inertia and torque, and the more kinetic energy it can store.

    Next time we’ll develop an equation which allows us to quantify the horsepower required to accelerate a flywheel.

opyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Flywheel Torque and Distribution of Mass

Moment of Inertia in a Flywheel

Monday, November 6th, 2017

    Last time we arrived at a general formula to compute the kinetic energy, KE, contained within the totality of a spinning flywheel made up of numerous parts.   Today we’ll discuss the terms in that formula, which encompasses a phenomenon of flywheels known as moment of inertia.

Moment of Inertia in a Flywheel

Moment of Inertia in a Flywheel

   

   The kinetic energy formula we’ve been working with is, again,

KE = ½ × Σ[m × r2] × ω2                           (1)

    The bracketed part of this equation makes reference to spinning flywheels comprised of one or more parts, and that’s what we’ll be focusing on today.   The symbol Σ is the Greek letter sigma, standard engineering shorthand notation used to represent the sum of all terms and mathematical operations contained within the brackets.

    Our illustration shows we have five parts to consider:  a hub, three spokes and a rim, and label them A, B, C, D, and E respectively.   Each part has its own mass, m, and is a unique distance, r, from the flywheel’s center of rotation.   The flywheel’s angular velocity is represented by ω.

   For our flywheel of parts A through E our expanded equation becomes,

Σ[m × r2] = [mA × rA2] + [mB × rB2] + [mC × rC2] + [mD × rD2] + [mE × rE2]      (2)

    Equation (2) represents the sum total of moments of inertia contained within our flywheel.  It’s a numerical representation of the flywheel’s degree of resistance to changes in motion.

    The more mass a flywheel has, the greater its moment of inertia.  When at rest this greater moment of inertia means it will take more effort to return it to motion.   But once in motion the flywheel’s greater moment of inertia will make it harder to stop.   That’s because there’s a lot of kinetic energy stored within its spinning mass, and the heavier a flywheel is, the more kinetic energy it contains.   In fact, for any given angular velocity ω, a large and heavy flywheel stores more kinetic energy than a smaller, lighter flywheel.

    But there’s more to a flywheel’s moment of inertia than just mass.   What’s really important is how that mass is distributed. We’ll get into that next time when we discuss torque.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Moment of Inertia in a Flywheel