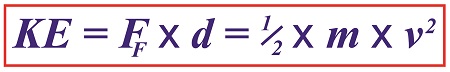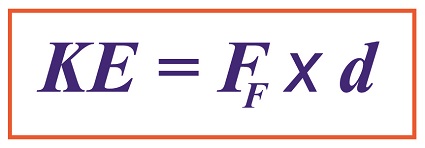Posts Tagged ‘frictional force’

What Came First? The Wheel or the Flywheel?

Monday, September 25th, 2017

   What came first?   The wheel or the flywheel?  Archeologists have been debating this question for decades.   One thing is certain, they both date back to prehistoric times.

What Came First? The Wheel or the Flywheel?

What Came First? The Wheel or the Flywheel?

   

   One of the oldest flywheel discoveries was a potter’s wheel, used to make pottery.   It’s a turntable made of stone or heavy wood that’s connected to a massive wheel by a spinning shaft.   Once the potter got the flywheel spinning with his hand or foot, the wheel’s heavy weight kept it in virtual perpetual motion, allowing the potter to concentrate on forming the clay he shaped with his hands.

   A potter’s wheel, or any other flywheel for that matter, takes a lot of initial effort to put into motion.   In other words, the potter must put a lot of his own muscles’ mechanical energy into the flywheel to get it moving.   That’s because its sheer weight binds it to the Law of Inertia and makes it want to stay at rest.

   But once the flywheel is in motion, the potter’s mechanical energy input is transformed into kinetic energy, the energy of motion.   The kinetic energy the potter produces by his efforts results in surplus energy stored within the flywheel.   Hence, the flywheel serves as a kinetic energy storage device, similar to a battery which stores electrical energy.   As long as the flywheel remains in motion, this stored energy will be used to keep the turntable spinning, which results in no additional mechanical energy needing to be exerted by the potter while forming pots.

   The flywheel’s stored energy also makes it hard to stop once it’s in motion.   But eventually the frictional force between the potter’s hands and the clay he works drains off all stored kinetic energy.

   Since the Industrial Revolution flywheels have been used to store kinetic energy to satisfy energy demands and provide a continuous output of power, which increases mechanical efficiency.

   Next time we’ll begin our exploration into the science behind flywheels and see how they’re used in diverse engineering applications.

 

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on What Came First? The Wheel or the Flywheel?

Combining Kinetic Energy Formulas to Calculate Velocity

Monday, June 6th, 2016

    As an engineering expert, I often use the fact that formulas share a single common factor in order to set them equal to each other, which enables me to solve for a variable contained within one of them.   Using this approach we’ll calculate the velocity, or speed, at which the broken bit of ceramic from the coffee mug we’ve been following slides across the floor until it’s finally brought to a stop by friction between it and the floor.   We’ll do so by combining two equations which each solve for kinetic energy in their own way.

    Last time we used this formula to calculate the kinetic energy, KE, contained within the piece,

KE = FF × d            (1)

and we found that it stopped its movement across the floor when it had traveled a distance, d, of 2 meters.

    We also solved for the frictional force, FF, which hampered its free travel, and found that quantity to be 0.35 kilogram-meters/second2.   Thus the kinetic energy contained within that piece was calculated to be 0.70 kilogram-meters2/second2.

    Now we’ll put a second equation into play.   It, too, provides a way to solve for kinetic energy, but using different variables.   It’s the version of the formula that contains the variable we seek to calculate, v, for velocity.   If you’ll recall from a previous blog, that equation is,

KE = ½ × m × v2          (2)

    Of the variables present in this formula, we know the mass, m, of the piece is equal to 0.09 kilograms.   Knowing this quantity and the value derived for KE from formula (1), we’ll substitute known values into formula (2) and solve for v, the velocity, or traveling speed, of the piece at the beginning of its slide.

 Combining Kinetic Energy Formulas to Calculate Velocity

Combining Kinetic Energy Formulas to Calculate Velocity

   

    The ceramic piece’s velocity is thus calculated to be,

KE = ½ × m × v2

0.70 kilogram-meters2/second2=  ½ × (0.09 kilograms) × v2

now we’ll use algebra to rearrange things and isolate v to solve for it,

v2 = 2 × (0.70 kilogram-meters2/second2) ÷ (0.09 kilograms)

v = 3.94 meters/second =12.92 feet/second = 8.81 miles per hour

Our mug piece therefore began its slide across the floor at about the speed of an experienced jogger.

Engineering expert

    This ends our series on the interrelationship of energy and work.   Next time we’ll begin a new topic, namely, how pulleys make the work of lifting objects and driving machines easier.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Combining Kinetic Energy Formulas to Calculate Velocity

Calculating Kinetic Energy By Means of the Work of Friction

Wednesday, May 25th, 2016

    My activities as an engineering expert often involve creative problem solving of the sort we did in last week’s blog when we explored the interplay between work and kinetic energy.   We used the Work-Energy Theorem to mathematically relate the kinetic energy in a piece of ceramic to the work performed by the friction that’s produced when it skids across a concrete floor.   A new formula was derived which enables us to calculate the kinetic energy contained within the piece at the start of its slide by means of the work of friction.   We’ll crunch numbers today to determine that quantity.

    The formula we derived last time and that we’ll be working with today is,

   

Calculating Kinetic Energy By Means of the Work of Friction

Calculating Kinetic Energy By Means of the Work of Friction

   

where, KE is the ceramic piece’s kinetic energy, FF is the frictional force opposing its movement across the floor, and d is the distance it travels before friction between it and the less than glass-smooth floor brings it to a stop.

    The numbers we’ll need to work the equation have been derived in previous blogs.   We calculated the frictional force, FF, acting against a ceramic piece weighing 0.09 kilograms to be 0.35 kilogram-meters/second2 and the measured distance, d, it travels across the floor to be equal to 2 meters.   Plugging in these values, we derive the following working equation,

KE = 0.35 kilogram-meters/second2 × 2 meters

KE = 0.70 kilogram-meters2/second2

    The kinetic energy contained within that broken bit of ceramic is just about what it takes to light a 1 watt flashlight bulb for almost one second!

    Now that we’ve determined this quantity, other energy quantities can also be calculated, like the velocity of the ceramic piece when it began its slide.   We’ll do that next time.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Calculating Kinetic Energy By Means of the Work of Friction

The Interplay of Work and Kinetic Energy

Thursday, May 12th, 2016

    We’ve been discussing the different forms energy takes, delving deeply into de Coriolis’ claim that energy doesn’t ever die or disappear, it simply changes forms depending on the tasks it’s performing.   Today we’ll combine mathematical formulas to derive an equation specific to our needs, an activity my work as an engineering expert frequently requires of me.   Our task today is to find a means to calculate the amount of kinetic energy contained within a piece of ceramic skidding across a concrete floor.   To do so we’ll combine the frictional force and Work-Energy Theorem formulas to observe the interplay between work and kinetic energy.

    As we learned studying the math behind the Work-Energy Theorem, it takes work to slow a moving object.   Work is present in our example due to the friction that’s created when the broken piece moves across the floor.   The formula to calculate the amount of work being performed in this situation is written as,

W = FF ×d              (1)

where, d is the distance the piece travels before it stops, and FF is the frictional force that stops it.

    We established last time that our ceramic piece has a mass of 0.09 kilograms and the friction created between it and the floor was calculated to be 0.35 kilogram-meters/second2.   We’ll use this information to calculate the amount of kinetic energy it contains.   Here again is the kinetic energy formula, as presented previously,

KE = ½ × m × v2      (2)

where m represents the broken piece’s mass and v its velocity when it first begins to move across the floor.

Interplay of Work and Kinetic Energy

The Interplay of Work and Kinetic Energy

   

    The Work-Energy Theorem states that the work, W, required to stop the piece’s travel is equal to its kinetic energy, KE, while in motion.   This relationship is expressed as,

KE = W            (3)

    Substituting terms from equation (1) into equation (3), we derive a formula that allows us to calculate the kinetic energy of our broken piece if we know the frictional force, FF, acting upon it which causes it to stop within a distance, d,

KE = FF × d

   Next time we’ll use this newly derived formula, and the value we found for FF in our previous article, to crunch numbers and calculate the exact amount of kinetic energy contained with our ceramic piece.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Interplay of Work and Kinetic Energy

Calculating the Force of Friction

Wednesday, April 27th, 2016

    Last time we introduced the frictional force formula which is used to calculate the force of friction present when two surfaces move against one another, a situation which I as an engineering expert must sometimes negotiate.   Today we’ll plug numbers into that formula to calculate the frictional force present in our example scenario involving broken ceramic bits sliding across a concrete floor.

   Here again is the formula to calculate the force of friction,

FF = μ × m × g

where the frictional force is denoted as FF, the mass of a piece of ceramic sliding across the floor is m, and g is the gravitational acceleration constant, which is present due to Earth’s gravity.   The Greek letter μ, pronounced “mew,” represents the coefficient of friction, a numerical value predetermined by laboratory testing which represents the amount of friction at play between two surfaces making contact, in our case ceramic and concrete.

    To calculate the friction present between these two materials, let’s suppose the mass m of a given ceramic piece is 0.09 kilograms, μ is 0.4, and the gravitational acceleration constant, g, is as always equal to 9.8 meters per second squared.

   

Calculating the Force of Friction

Calculating the Force of Friction

   

    Using these numerical values we calculate the force of friction to be,

FF = μ × m × g

FF = (0.4) × (0.09 kilograms) × (9.8 meters/sec2)

FF = 0.35 kilogram meters/sec2

FF = 0.35 Newtons

    The Newton is shortcut notation for kilogram meters per second squared, a metric unit of force.   A frictional force of 0.35 Newtons amounts to 0.08 pounds of force, which is approximately equivalent to the combined stationary weight force of eight US quarters resting on a scale.

    Next time we’ll combine the frictional force formula with the Work-Energy Theorem formula to calculate how much kinetic energy is contained within a single piece of ceramic skidding across a concrete floor before it’s brought to a stop by friction.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on Calculating the Force of Friction

The Frictional Force Formula

Thursday, April 14th, 2016

    Last time we introduced the force of friction, another force in our ongoing discussion about changing forms of energy, and we learned that it’s often a counterproductive force which design engineers and engineering experts such as myself must work to minimize in order to optimize functionality of devices we’re designing.   Today we’ll introduce the frictional force formula, which computes the amount of friction present when two surfaces meet.

    To demonstrate frictional force, we’ve been working with the example of a shattered mug’s broken ceramic pieces and watching their progress as they slide across a concrete floor.   They eventually come to a stop not too far from the point where the mug shattered, because friction causes them to stop.   The mass of the ceramic pieces in combination with the downward pull of gravity causes the broken bits to “bear down” on the floor, thereby maximizing contact and creating friction.

    At first glance the floor and mugs’ surfaces may appear slippery smooth, but when viewed under magnification we see that both actually contain many peaks and valleys.   The peaks of one surface project into the valleys of the other and it’s fight, fight, fight for the ceramic pieces to continue their progress across the floor.   The strength of the frictional force acting upon the pieces is a factor of their individual weights coupled with the roughness of the two surfaces coming into contact — the shattered pieces and the floor.   If friction didn’t exist and no other impediments were in the way, the pieces might travel to the next state before stopping!

 Frictional Force Resists Motion

 Frictional Force Resists Motion

   

    Last time we introduced Charles-Augustin de Coulomb, a scientist whose work with friction led to the later development of a formula to calculate it.   It’s presented here, and frictional force is denoted as FF,

FF = μ × m × g

where, m is the mass of an object making contact with another surface and g is the gravitational acceleration constant, which is due to the force of Earth’s gravity.   The Greek letter μ, pronounced “mew,” represents the coefficient of friction, a number.   Numerical values for μ were determined by laboratory testing and are recorded in engineering books for many combinations of materials, including rubber on concrete, leather on steel, wood on aluminum, and our own example of ceramic on concrete.

    Next time we’ll plug the numbers that apply to our ceramic-on-concrete example into the friction formula and calculate the frictional force at play.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Frictional Force Formula

Coulomb’s Frictional Force

Monday, April 4th, 2016

    Humans have been battling the force of friction since the first cave man built the wheel.   Chances are his primitive tools produced a pretty crude wheel that first go-around and the wheel’s surfaces were anything but smooth, making its usefulness less than optimal.   As an engineering expert, I encounter these same dynamics when designing modern devices.   What held true for the cave man holds true for modern man, friction is often a counterproductive force which design engineers must work to minimize.   Today we’ll learn about frictional force and see how it impacts our example broken coffee mug’s scattering pieces, and we’ll introduce the man behind friction’s discovery, Charles-Augustin de Coulomb.

Coulomb's Work on Friction

Charles-Augustin de Coulomb

   

    Last time we learned that the work required to shatter our mug was transformed into the kinetic energy which propelled its broken pieces across a rough concrete floor.   The broken pieces’ energetic transformation will continue as the propelling force of kinetic energy held within them is transmuted back into the work that will bring each one to an eventual stop a distance from the point of impact.   This last source of work is due to the force of friction.

    In 1785 Charles-Augustin de Coulomb, a French physicist, discovered that friction results when two surfaces make contact with one another, and that friction is of two types, static or dynamic.   Although Leonardo Da Vinci had studied friction hundreds of years before him, it is Coulomb who is attributed with doing the ground work that later enabled scientists to derive the formula to calculate the effects of friction.   Our example scenario illustrates dynamic friction, that is to say, the friction is caused by one of the surfaces being in motion, namely the mug’s ceramic pieces which skid across a stationary concrete floor.

    While in motion, each of the mug’s broken pieces has its own unique velocity and mass and therefore a unique amount of kinetic energy.   The weight of each piece acts as a vertical force pushing the piece down “into” the floor, this due to the influence of Earth’s gravitational pull, that is, the force of gravity.

    Friction is created by a combination of factors, including the ceramic pieces’ weights and the surface roughness of both the pieces themselves and the concrete floor they skid across.   At first glance the floor and ceramic mug’s surfaces may appear slippery smooth, but when viewed under magnification it’s a whole different story.

    Next time we’ll examine the situation under magnification and we’ll introduce the formula used to calculate friction along with a rather odd sounding variable, mu.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Coulomb’s Frictional Force