|
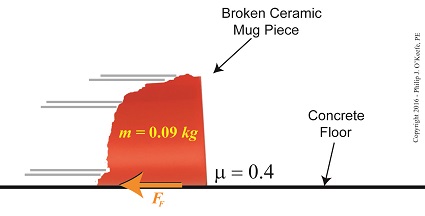
Last time we introduced the frictional force formula which is used to calculate the force of friction present when two surfaces move against one another, a situation which I as an engineering expert must sometimes negotiate. Today we’ll plug numbers into that formula to calculate the frictional force present in our example scenario involving broken ceramic bits sliding across a concrete floor. Here again is the formula to calculate the force of friction, FF = μ × m × g where the frictional force is denoted as FF, the mass of a piece of ceramic sliding across the floor is m, and g is the gravitational acceleration constant, which is present due to Earth’s gravity. The Greek letter μ, pronounced “mew,” represents the coefficient of friction, a numerical value predetermined by laboratory testing which represents the amount of friction at play between two surfaces making contact, in our case ceramic and concrete. To calculate the friction present between these two materials, let’s suppose the mass m of a given ceramic piece is 0.09 kilograms, μ is 0.4, and the gravitational acceleration constant, g, is as always equal to 9.8 meters per second squared.
Calculating the Force of Friction
Using these numerical values we calculate the force of friction to be, FF = μ × m × g FF = (0.4) × (0.09 kilograms) × (9.8 meters/sec2) FF = 0.35 kilogram meters/sec2 FF = 0.35 Newtons The Newton is shortcut notation for kilogram meters per second squared, a metric unit of force. A frictional force of 0.35 Newtons amounts to 0.08 pounds of force, which is approximately equivalent to the combined stationary weight force of eight US quarters resting on a scale. Next time we’ll combine the frictional force formula with the Work-Energy Theorem formula to calculate how much kinetic energy is contained within a single piece of ceramic skidding across a concrete floor before it’s brought to a stop by friction. Copyright 2016 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Tags: coefficient of friction, Earth's gravity, engineering expert, force of friction, friction, frictional force, frictional force formula, gravitational acceleration constant, kinetic energy, Newtons, weight force, work-energy theorem