Posts Tagged ‘law of conservation of energy’

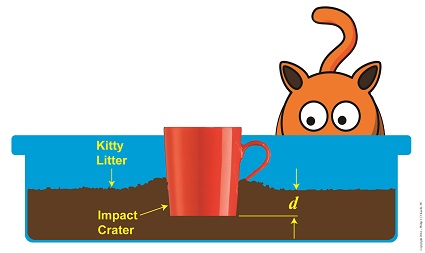
When Kinetic Energy Meets With Opposing Force

Tuesday, March 1st, 2016

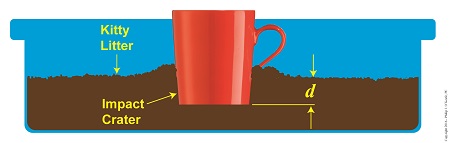
    Objects in motion inevitably meet with opposing forces, a theme which I frequently encounter in my work as an engineering expert.   Today we’ll calculate the opposing force our exemplar coffee mug meets when it falls into a pan of kitty litter, thus transforming its freefalling kinetic energy into the work required to move through clay litter.

    Let’s revisit the Work-Energy Theorem formula, whose terms were explained in last week’s blog,

F × d = – ½ × m × v12          (1)

    The left side of this equation represents the mug’s work to move through the litter, while the right side represents its kinetic energy, which it gained through freefall.   To solve for F, the amount of force acting in opposition to the mug’s mass m as it plows a depth d into the litter, we’ll isolate it on one side of the equation, as shown here,

F = [- ½ × m × v12 ] ÷ d          (2)

    So how do we solve for F when we don’t know the value of v1, the mug’s freefall velocity at impact?   We’ll use the fact that The Law of Conservation of Energy tells us that all energies are equal, and we’ll eliminate the part of Equation (2) that contains this unknown variable, that is, the right side of the equation which deals with kinetic energy.   In its place we’ll substitute terms which represent the mug’s potential energy, that is, the latent energy held within it as it sat upon the shelf prior to falling.  Equation (2) then becomes,

F = [- m × g × h] ÷ d           (3)

where g is the Earth’s acceleration of gravity factor, a constant equal to 9.8 meters/sec2 , and h is the height from which the mug fell.

Kinetic Energy Meets With Opposing Force

Kinetic Energy Meets With Opposing Force

   

    So if we know the mug’s mass, the distance fallen, and the depth of the crater it made in the litter, we can determine the stopping force acting upon it at the time of impact.   It’s time to plug numbers.

    Let’s say our mug has a mass of 0.25 kg, it falls from a height of 2 meters, and it makes a crater 0.05 meters deep.   Then the stopping force acting upon it is,

F = [- (0.25 kg) × (9.8 meters/sec2) × (2 meters)] ÷ (0.05 meters)

=  – 98 Newtons

    The mug was subjected to -98 Newtons, or about -22 pounds of opposing force when it fell into the litter, that resistance being presented by the litter itself.

    Next time we’ll see what happens when our mug strikes a hard surface that fails to cushion its impact.    Energy is released, but where does it go?

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on When Kinetic Energy Meets With Opposing Force

Combining the Law of Conservation of Energy and Work-Energy Theorem

Thursday, February 18th, 2016

     It’s not uncommon in my work as an engineering expert to encounter a situation in which I’m missing information.   At that point I’ve got to find a creative solution to working the problem.   We’ll get creative today when we combine the  Law of Conservation of Energy and the Work-Energy Theorem to get around the fact that we’re missing a key quantity to calculate forces exerted upon the falling coffee mug we’ve been following in this blog series.

    Last time we applied the Work-Energy Theorem to our mug as it came to rest in a pan of kitty litter.   Today we’ll set up the Theorem formula to calculate the force acting upon it when it meets the litter.   Here’s where we left off,

 F × d = –½ × m × v12

where, F is the force acting to slow the progress of the mug with mass m inside the litter pan.   The mug eventually stops and comes to rest in a crater with a depth, d.   The left side of the equation represents the mug’s work expenditure, as it plows through the litter, which acts as a force acting in opposition to the mug’s travel.

Work-Energy Theorem Applied To A Falling Coffee Mug

Kinetic Energy Meets Up With Displacement

   

    The right side of the equation represents the mug’s kinetic energy, which it gained in freefall, at its point of impact with the litter.   The right side is in negative terms because the mug loses energy when it meets up with this opposing force.

    Let’s say we know the values for variables d and m, quantities which are easily measured.   But the kinetic energy side of the equation also features a variable of unknown value, v1, the mug’s velocity upon impact.   This quantity is difficult to measure without sophisticated electronic equipment, something along the lines of a radar speed detector used by traffic cops.   For the purpose of our discussion we’ll say that we don’t have a cop standing nearby to measure the mug’s falling speed.

    If you’ll recall from past blog discussions, the Law of Conservation of Energy states that an object’s — in this case our mug’s — kinetic energy is equal to its potential energy.   It’s this equivalency relationship which will enable us to solve the equation and work around the fact that we don’t have a value for v1.

    We’ll do the math and plug in the numbers next time.

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Combining the Law of Conservation of Energy and Work-Energy Theorem

Applying the Work-Energy Theorem to Falling Objects

Monday, February 8th, 2016

    So far we’ve applied the Work-Energy Theorem to a flying object, namely, Santa’s sleigh, and a rolling object, namely, a car braking to avoid hitting a deer.   Today we’ll apply the Theorem to a falling object, that coffee mug we’ve been following through this blog series.   We’ll use the Theorem to find the force generated on the mug when it falls into a pan of kitty litter.   This falling object scenario is one I frequently encounter as an engineering expert, and it’s something I’ve got to consider when designing objects that must withstand impact forces if they are dropped.

   

Applying the Work-Energy Theorem to Falling Objects

Applying the Work-Energy Theorem to Falling Objects

   

    Here’s the Work-Energy Theorem formula again,

F × d = ½ × m × [v22 – v12]

where F is the force applied to a moving object of mass m to get it to change from a velocity of v1 to v2 over a distance, d.

    As we follow our falling mug from its shelf, its mass, m, eventually comes into contact with an opposing force, F, which will alter its velocity when it hits the floor, or in this case a strategically placed pan of kitty litter.   Upon hitting the litter, the force of the mug’s falling velocity, or speed, causes the mug to burrow into the litter to a depth of d.   The mug’s speed the instant before it hits the ground is v1, and its final velocity when it comes to a full stop inside the litter is v2, or zero.

    Inserting these values into the Theorem, we get,

F × d = ½ × m × [0 – v12]

F × d = – ½ × m × v12

    The right side of the equation represents the kinetic energy that the mug acquired while in freefall.   This energy will be transformed into Gaspard Gustave de Coriolis’ definition of work, which produces a depression in the litter due to the force of the plummeting mug.   Work is represented on the left side of the equal sign.

    Now a problem arises with using the equation if we’re unable to measure the mug’s initial velocity, v1.   But there’s a way around that, which we’ll discover next time when we put the Law of Conservation of Energy to work for us to do just that.

 

Copyright 2016 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

   

____________________________________

 

Tags: , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury | Comments Off on Applying the Work-Energy Theorem to Falling Objects

Joule’s Dynamo – The Joule Heating Effect

Saturday, October 24th, 2015

      As an engineering expert with 14 years’ electric utility experience, I’ve dealt with all types of electrical power generators, including many similar to the dynamo that James Prescott Joule used in his Experiment With Electricity.   Today we’ll look inside Joule’s dynamo and see how it contributed to creating electricity as well as another of Joule’s discoveries, the Joule Heating Effect.

Dynamo-Circa Early 19th Century

Dynamo-Circa Early 19th Century

      In Joule’s Experiment With Electricity, the dynamo was powered by a steam engine, which enabled the dynamo’s shaft to spin.    As it spun, the magnet located inside the dynamo also spun, thus creating a rotating magnetic field that surrounded the dynamo’s internal copper wire coils.

      The interaction between the magnetic field and wire produced electric current which flowed inside the coils.   The current ultimately made its way out of the dynamo by way of external wires, to which any number of devices could be powered when attached.   The net result was the engine’s mechanical energy had been converted into electrical.   To learn more about the process of producing electricity with magnets see my blog on, Coal Power Plant Fundamentals – The Generator.

      As electrical energy flowed through the dynamo’s wiring, some of it was converted into heat energy.   This was due to resistance posed by impurities present in the makeup of the wire, impurities which served to impede the overall flow of electric current.   When electrons flowing through the wire collided with these impediments, they caused heat to build up inside the wire, a phenomenon which came to be known as the Joule Heating Effect.   To read more on electrical resistance and Joule heating go to my blog, Wire Size and Electric Current.

      The net result of Joule’s Experiment With Electricity was to further prove the link between chemical, heat, mechanical and electrical energies as set out in the Law of Conservation of Energy.   And I suspect that knowledge was later put to use by Joule’s family for the betterment of their brewery business.

      Next time we’ll use Joule’s experimental findings in conjunction with de Coriolis’ Kinetic Energy Formula to quantify the energy of the falling coffee mug we’ve been watching.

Copyright 2015 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

Tags: , , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Joule’s Dynamo – The Joule Heating Effect

Calculating Velocity — de Coriolis’ Kinetic Energy Formula

Monday, September 28th, 2015

      Last time we introduced Gaspard-Gustave de Coriolis’ formula to compute kinetic energy.  Today we’ll use it to determine the speed of descent, or velocity, of the coffee mug we’ve been watching closely in the last few blogs.  To calculate the mug’s velocity, we must bear in mind physicist Julius Robert von Mayer’s assertion that all forms of energy are interrelated, and in fact interchangeable, because energy can neither be created nor destroyed, it can only change forms.  For a refresher, see The Law of Conservation of Energy.

      Let’s now put a practical spin on this concept and apply it to our coffee mug’s free fall to the floor.  Once again, de Coriolis’ formula,

KE = ½ × m × v2                                               (1)

where m is the mass of our falling object and v its velocity.  The ½ is an unchanging, constant term that’s present due to the mathematical Rules of Integration governing integral calculus.  Calculus and its derivations are beyond the scope of this blog, but if you’re interested in pursuing this, follow this link to, The Physics Hypertextbook – Kinetic Energy.

      According to von Mayer’s Law, at the precise instant before the mug hits the floor its kinetic energy, KE, is equal to the potential energy, PE, it possessed when it rested passively on the shelf.  Stated another way, the instant before the mug makes contact with the floor, all its potential energy will have been converted into kinetic.

      The mug’s PE was calculated previously to be equal to 4.9 kg • meter2/second2.  See Computing Potential Energy for a review.  Knowing this, the mathematical relationship between the mug’s potential and kinetic energies is expressed as,

PE = KE = 4.9 kg • meter2/second2                         (2)

      By substituting this mathematical representation for KE into equation (1) we arrive at,

4.9 kg • meter2/second2 = ½ × m × v2                   (3)

We also know the mug’s mass, m, to be equal to 2.6 kilograms, so integrating that into the right side of equation (3) it becomes,

4.9 kg • meter2/second2 = ½ × ( 0.25kg) × v2         (4)

That leaves the mug’s velocity, v2, as the only remaining unknown term.  We’ll use algebra to isolate this variable by dividing both sides of equation (4) by ½ × ( 0.25kg).

(4.9 kg • meter2/second2) ÷ [½ × ( 0.25kg)] = v2

39.20 meter2/second2 = v2

Finally, we’ll take the square root of the equation to place it in terms of v.

6.26 meters/second = v

The mug’s velocity an instant before impact equates to 6.26 meters/second, or almost 21 feet per second.

mechanical engineering expert witness falling objects

      Next time we’ll discuss a metric unit used to measure energy known as the Joule and discover the man behind it.

Copyright 2015 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

Tags: , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Calculating Velocity — de Coriolis’ Kinetic Energy Formula

The Law of Conservation of Energy

Wednesday, September 2nd, 2015

      Last time we calculated the potential energy hidden within a coffee mug resting on a shelf.   The concept of a passive object possessing energy may not be something all readers can identify with, but the secret behind that mug’s latent energy lies within The Law of Conservation of Energy, the topic we’ll be discussing today.

      Julius Robert von Mayer, a German physicist of the mid 19th Century, is the man behind the Law.   He posited that energy cannot be created or destroyed, it can only be transferred from one object to another or converted from one form of energy to another.   Forms of energy include potential, kinetic, heat, chemical, mechanical, and electrical, all of which have the ability to become another form of energy.

      Let’s take our coffee mug for example.   Where did its potential energy come from?   Ultimately, from the radiant energy emitted by the sun.   The sun’s radiant energy was absorbed by plants and then converted to chemical energy through the process of photosynthesis, enabling them to grow.   When they were later eaten by humans and other animals, the plants’ chemical energy became incorporated into their bodies’ cells, including the arm muscles used to lift the mug to the shelf.

      In the act of lifting the cup, the arm’s muscle cells converted their own chemical energy into mechanical energy.   And because lifting a mug to a shelf is work, for some of us greater than others, some of the arm’s chemical energy became heat energy which was lost to the environment.

      Because of the elevated perch provided to the mug by the arm, which was in direct defiance of Earth’s gravitational pull, the arm muscles’ mechanical energy was transferred to the mug and converted to latent potential energy, because without that shelf to support it, the mug would fall to the ground.   The mug’s potential energy would realize its full potential if it should be sent crashing to the floor, at which time it would become another form of energy.   The mischievous orange kitty seems to have just that in mind.

engineering expert witness falling objects

      We’ll talk more about the mug’s potential energy being converted to other forms next time.

Copyright 2015 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

Tags: , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Law of Conservation of Energy

Determining the Gear Train Tradeoff of Torque vs. Speed, Part One

Friday, August 15th, 2014

      Hold onto your hats, we’re going to deal with a lot of equations today!

      Last time we used flashbacks to previous blogs in this series to revisit key equations in our ongoing discussion of gear trains and torque.   We also introduced The Law of Conservation of Energy in conjunction with five equations that together demonstrate how when increasing torque by use of a simple gear train, we do so at the cost of speed.

      Those five equations are:

R = NDriven ÷  NDriving =  nDriving ÷ nDriven (1)
TDriving ÷ TDriven =  DDriving ÷ DDriven (2)
TDriving = [HPDriving ÷ nDriving] × 63,025 (3)
TDriven = [HPDriven ÷ nDriven] × 63,025 (4)
HPDriving =  HPDriven (5)

where, R is the gear ratio, N the number of gear teeth, n the gear’s rotational speed, T the torque, D the gear pitch radius, and HP is the horsepower transmitted by the gears.

Mechanical Engineering Expert Witness

      As we work the equations, keep in mind that our ultimate objective is to find a way to link together (1) and (2), the equations dealing with gear torque and speed.   Once we accomplish this we’ll see how increased torque is obtained at the cost of speed.   But because there are no common terms between equations (1) and (2), our first step is to develop one.

      Developing a link between equations (1) and (2) is a process that begins with combining equations (2), (3), and (4).

TDriving ÷ TDriven =  DDriving ÷ DDriven (2)
TDriving = [HPDriving ÷ nDriving] × 63,025 (3)
TDriven = [HPDriven ÷ nDriven] × 63,025 (4)

      The common terms in these three equations are TDriving and TDriven, so we’ll manipulate things in order to group them together.   We’ll substitute equation (3) for the TDriving term in equation (2), and substitute equation (4) for the TDriven term in equation (2).   We are now able to link all three equations to get:

{[HPDriving ÷ nDriving] × 63,025} ÷  {[HPDriven ÷ nDriven] × 63,025}

                                                                                        = DDriving ÷ DDriven         (6)

      Now let’s go a step further to simplify equation (6).   From equation (5) we know that the driving and driven gear horsepowers are equal.   So, in equation (6), the HPDriving and HPDriven cancel out, along with the two 63,025 terms, allowing us to arrive at equation (7):

{[HPDriving ÷ nDriving] × 63,025} ÷  {[HPDriven ÷ nDriven] × 63,025}

                                                                             = DDriving ÷ DDriven

nDriven ÷ nDriving = DDriving ÷ DDriven (7)

      Next week we’ll use equation (7) to link together R, N, n, of equation (1) with D and T of equation (2) and in so doing disclose mathematically the tradeoff between torque and speed, then apply our findings to an example.

_______________________________________

Tags: , , , , , , , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Determining the Gear Train Tradeoff of Torque vs. Speed, Part One